Полигоны, гистограммы, эмпирические функции распределения.
Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которой служат частичные интервалы длиной h, а высоты равны отношению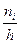 
. Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки n. В случае гистограммы относительных частот по оси ординат откладываются нормированные относительные частоты 
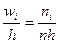, на оси абсцисс – частичные интервалы (рис.1). Площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.
Полигоном частот называют ломаную линию, отрезки которой соединяют точки (xi, ni), i=1, 2, … k. Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат – соответствующие им частоты ni и соединяют точки (xi, ni) отрезками прямых (рис. 2).
Рис.1. Гистограмма относительных частот
Рис.2. Полигон частот
Полигон относительных частот строится аналогично, за исключением того, что на оси ординат откладываются относительные частоты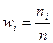 
(рис. 3). Для построения полигона нормированных относительных частот на оси ординат откладывают нормированные относительные частоты .
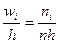Рис.3. Полигон относительных частот
Эмпирической функцией распределения называется функция, вычисляемая для любого значения х по формуле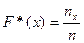 
, где n – объем выборки, 
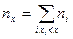– количество вариант, значения которых меньше, чем х. Для нашей выборки
1) F*(x) = 0, для всех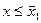 
.
2) 
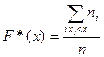для 
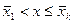
3) F* (x) = 1, для всех 
.
Откладывая на оси абсцисс точки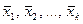 
, а на оси ординат отрезки, параллельные оси абсцисс, получим ступенчатую функцию (рис. 4).
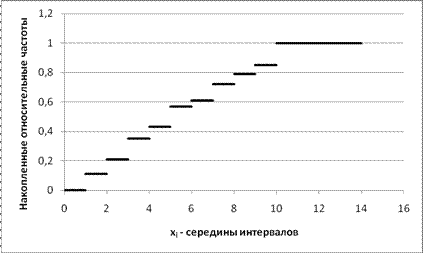
Рис. 4. Эмпирическая функция распределения F(x)
6. Вопросы для самопроверки
1. Определение достоверного (невозможного) события. Классическое определение вероятности. Геометрическая вероятность.
2. Теорема сложения вероятностей. Теорема умножения вероятностей.
3. Формула полной вероятности.
4. Виды случайных событий: понятия несовместных и независимых событий.
5. Основные понятия теории вероятностей: аксиомы теории вероятностей.
6. Вероятность произведения событий. Условная вероятность.
7. Определения вероятностей противоположного события. Полная группа.
8. Теорема сложения и умножения вероятностей: вероятность появления хотя бы одного события.
9. Определения закона распределения вероятностей дискретной случайной величины.
10. Определение математического ожидания дискретной случайной величины.
11. Числовые характеристики дискретных случайных величин: дисперсия, среднее квадратичное отклонение.
12. Квантиль. Начальные и центральные моменты.
13. Законы распределения вероятностей дискретных случайных величин: формула Пуассона.
14. Асимптотические приближения схемы Бернулли.
15. Биномиальный закон распределения вероятностей дискретных случайных величин. Формула Бернулли. Схема независимых испытаний.
16. Формулы Байеса.
17. Определения плотности распределения вероятностей непрерывной случайной величины. Свойства плотности.
18. Функция распределения вероятностей непрерывной случайной величины. Связь с плотностью.
19. Законы распределения вероятностей непрерывных случайных величин: равномерное распределение.
20. Законы распределения вероятностей непрерывных случайных величин: нормальное распределение.
21. Законы распределения вероятностей дискретных случайных величин: интегральная формула.
22. Определение нормального закона распределения случайной величины.
23. Неравенство Чебышева.
24. Теорема Чебышева.
25. Центральная предельная теорема.
26. Статистическое определение вероятности.
27. Определение статистического распределения выборки. Генеральная совокупность. Выборочный метод.
28. Характеристики вариационного ряда. Мода. Частоты. Относительные частоты.
29. Определение точечных оценок параметров распределения. Состоятельная оценка. Несмещенная оценка математического ожидания.
30. Средняя арифметическая.
31. Выборочная дисперсия и среднее квадратичное отклонение.
32. Полигон частот.
33. Интервальные оценки параметров распределения. Доверительный интервал.
34. Непрерывное распределение признака. Определение вариационного ряда для непрерывного признака X.
35. Гистограмма частот.
36. Статистическая связь. Корреляционная зависимость. Уравнение линейной регрессии.
37. Коэффициент корреляции.
38. Определение коэффициента регрессии.
39. Определение статистической гипотезы. Конкурирующая гипотеза. Ошибки первого и второго рода.
40. Уровень значимости. Критические точки — односторонние и двусторонние.
41. Критерии проверки гипотез.
42. Метод статистических испытаний.
43. Случайная функция. Сечение случайной функции. Реализация случайной функции.
44. Характеристики случайной функции. Математическое ожидание. Его свойства.
45. Характеристики случайной функции. Дисперсия. Её свойства.
46. Характеристики случайной функции. Корреляционная функция. Её свойства.
47. Случайные процессы. Статистические характеристики случайных процессов.
48. Стационарный случайный процесс.
49. Марковские процессы.
50. Вероятность и информация.
Список литературы
1. Гмурман В.Е. Теория вероятностей и математическая статистика. — М.: Высшая школа, 2001.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. — М.: Высшая школа, 2001.
3. Кабанова И.Е. Теория вероятностей и математическая статистика. Курс лекций. —Дубна, 1996.
4. Петровский Б. В.. Популярная медицинская энциклопедия. — Таллин: Советская Энциклопедия, 1993.
5. Мамонов С. Г.. Общая биология. — М.: Высшая школа, 1996.
6. Гилберт С. Ф.. Биология развития. — М.: Мир, 1993.
7. Закс Г. Строение и деятельность человеческого тела. — СПб: Издательство В. В.Битнера, 1905.
8. Семенов Э. В. Анатомия и физиология человека. — М.: АНМИ, 1995.
9. Фомин Н. А. Физиология человека. — М.: Просвещение; ВЛАДОС, 1995.
10. Бойчук Н. В. Курс гистологии. — Казань: Поволжский книжный центр, 1995.
11. Зенгбум П. Молекулярная и клеточная биология. — М.: Мир, 1982.
12. Аккерман Ю. Биофизика. — М.: Мир, 1964.
13. Циммерман М. Физиология человека. — М.:.Мир, 1996.
14. Интернет-источник: http://www.malysham.info/.
15. Интернет-источник: http:.//www.obsheniye.ru/article/index.html.
16. Интернет-источник: http://www.obsheniye.ru/article/self appraisal/index.html.
17. Гальперин В.М., Игнатьев СМ. Микро- и макроэкономика. — СПб.: Экономическая школа, 2002.
18. Ивашев-Мусатов О.С. Теория вероятностей и математическая статистика. — М.: Наука, 1979.
19. Мазный Г.Л., Прогулова Т.Б. Методическое пособие к курсовому проектированию по ВМ и информатике. —Дубна: Кафедра ВМ и САУ. 1996.
20. Кабанова Е.И. Теория вероятностей и математическая статистика. Курс лекций. —Дубна: Международный университет природы, общества и человека «Дубна», 1996.
21. http://www.bank-city.ru/main/749-makrqjekonomicheskie-problemy.html
22. Колмогоров А.Н., Журбенко И.Г., Прохоров А.В. Введение в теорию вероятностей. — 2-е изд. — М.: Физматлит, 1995.
23. Биологический энциклопедический словарь. — М.: Сов. энциклопедия, 1989.
24. Амблер Т. Практический маркетинг. — СПб: Питер, 1999.
25. Афанасьев М.П. Маркетинг: стратегия и практика фирмы. — М: Финстатинформ, 1995.
26. http://revolution.allbest.ru/Keoi;raphv/00002007_0.html
27. http://articles.excelion.ruyscience/geografy/64224462.html
28. Буримов Ю. Г., Копылов А. С, Орлов А. В. Бурение верхних интервалов глубоких скважин большого диаметра. — М, Недра, 1975.
29. Розанов Ю.А. Теория вероятностей, случайные процессы и математическая статистика. М.: Наука, 1985.
30. Ширяев А.Н. Вероятность. -М.: Наука, 1989.
31. Статистика: Автомобили и цены, журнал; //http://www7statistics.ru
32. Чавлеишвили М. П. Задачи по математической статистике: Учеб. пособие. — Дубна: Международный университет природы, общества и человека «Дубна», 2003
33. Бочаров П.П, Печинкин А.В Теория вероятностей. Математическая статистика — М.: Гардарика, 1998
34. Ершова И.В. Предпринимательское право: Москва, 2003.
35. Интернет-сайт: http://ru.wikipedia.org.
36. Свешникова А. А. Сборник задач по теории вероятностей, математической статистике и теории случайных функций. — М.: Наука, 2002.
37. http://bankrabot.com/workywork 70036.html.
38. http://www.solis-seeds.rii/secure_4
39. Http://ru.wikipedia.org/wiki/CoTOBaM_CBM3b
40. Художественная школа. М.: Издательство Эксмо, 2003. — 528 с.
41. Биологический энциклопедический словарь. — М.: Сов. энциклопедия, 1989.
42. http://www.5ballov.ru/referats/preview/71747
43. http://revolution.allbest.ru/economy/00006347_0.html
44. http://www.math-pr.com/stst_1v_1.php
45. http://www.math-pr.com/stst_3v_1.php
Дата добавления: 2015-09-11; просмотров: 9218;