Инструкция по выполнению курсовой работы.

Обработку выборки следует начать с вычисления ее числовых характеристик: выборочного среднего, выборочной и исправленной дисперсий, среднего квадратичного отклонения, моды и медианы. Эти параметры вычисляются отдельно для каждой из переменных X и Y. Выборочное среднее— среднее арифметическое значений случайной величины, принимаемых в выборке, является несмещенной оценкой математического ожидания генеральной совокупности. Выборочное среднее несгруппированной выборки (x₁ x₂ … x_n) объема n вычисляется по формуле: 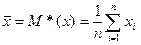. Выборочная дисперсия 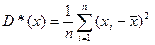является смещенной оценкой генеральной дисперсии, исправленная дисперсия 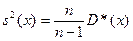— несмещенной оценкой генеральной дисперсии. Среднее квадратичное отклонение 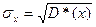, исправленное среднее квадратичное отклонение 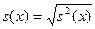. Мода М₀ – варианта (значение x_i), имеющая наибольшую частоту, медиана Me — варианта, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно (n = 2k + 1), то Me = x_k+1, а при четном n (n = 2k) .

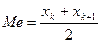Затем следует вычислить параметры, характеризующие связь между величинами X и Y — ковариацию и коэффициент корреляции. Ковариацию можно вычислить по формуле 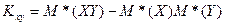, 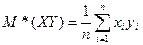. Коэффициент корреляции 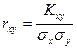— это показатель взаимного вероятностного влияния двух случайных величин. Коэффициент корреляции r_xyможет принимать значения от -1 до +1. Если абсолютное значение находится ближе к 1, то это свидетельство сильной связи между величинами, а если ближе к 0 — то, это говорит о слабой связи или ее отсутствии. Если абсолютное значение r_xyравно единице, то можно говорить о функциональной связи между величинами, то есть одну величину можно выразить через другую посредством математической функции.

Все перечисленные характеристики можно вычислить с помощью встроенных функций в программе Microsoft Excel. Для этого в первые столбцы введите заданные значения X и Y (столбец А — значения X, столбец В — значения Y). При проведении сложного статистического анализа можно упростить процесс и сэкономить время, используя надстройку «Пакет анализа». Для анализа данных с помощью этого пакета следует указать входные данные и выбрать параметры; расчет будет выполнен с помощью подходящей статистической или инженерной макрофункции, а результат будет помещен в выходной диапазон. Некоторые инструменты позволяют представить результаты анализа в графическом виде. Для доступа к этим инструментам нажмите кнопку Анализ данных в группе Анализ на вкладке Данные.

Если кнопка Анализ данных недоступна, необходимо загрузить надстройку «Пакет анализа». Загрузка пакета анализа:

1. Щелкните значок Кнопка Microsoft Office , а затем щелкните Параметры Excel.

2. Перейдите на вкладку Надстройки, а затем в поле Управление выберите Надстройки Excel.

3. Нажмите кнопку Перейти.

4. В поле Доступные надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.

Совет. Если надстройка Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор и найдите ее самостоятельно.

Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да для его установки.)

В диалоговом окне Анализ данных выберите инструмент анализа в списке Инструменты анализа, а затем нажмите кнопку ОК.

Введите необходимые данные и задайте параметры для выбранного инструмента анализа, а затем нажмите кнопку ОК.

Для просмотра описания и сведений по работе с диалоговым окном для каждого инструмента щелкните его название в следующем списке:

• Дисперсионный анализ

• Корреляция

Функции КОРРЕЛ и ПИРСОН вычисляют коэффициент корреляции между двумя переменными измерений, когда для каждой переменной измерение наблюдается для каждого субъекта N (пропуск наблюдения для субъекта приводит к игнорированию субъекта в анализе). Корреляционный анализ иногда применяется, если для каждого субъекта N есть более двух переменных измерений. В результате выводится таблица, корреляционная матрица, показывающая значение функции КОРРЕЛ (или ПИРСОН) для каждой возможной пары переменных измерений.

Коэффициент корреляции, как и ковариационный анализ, характеризует степень, в которой два измерения «изменяются вместе». В отличие от ковариационного анализа коэффициент корреляции масштабируется таким образом, что его значение не зависит от единиц, в которых выражены переменные двух измерений (например, если вес и высота являются двумя измерениями, значение коэффициента корреляции не изменится после перевода веса из фунтов в килограммы). Любое значение коэффициента корреляции должно находиться в диапазоне от -1 до +1 включительно.

• Ковариация

Ковариационный анализ вычисляет значение функции КОВАР для каждой пары переменных измерений (напрямую использовать функцию КОВАР вместо ковариационного анализа имеет смысл при наличии только двух переменных измерений, то есть при N=2 — наш случай). Элемент по диагонали таблицы, возвращаемой после проведения ковариационного анализа в строке i столбец i является ковариационным анализом i-ой переменной измерения с самой собой; это дисперсия для данной переменной, вычисляемая функцией ДИСПР.

Ковариационный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть большие значения из одного набора данных связаны с большими значениями другого набора (положительная ковариация) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная ковариация), или данные двух диапазонов никак не связаны (ковариация близка к нулю).

В нашем случае этот инструмент выдает значения выборочных дисперсий по X и Y и значение ковариации - корреляционного момента.

• Описательная статистика

Инструмент анализа «Описательная статистика» применяется для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных, в т.ч. значения средней выборочной, исправленной выборочной дисперсии, исправленного среднеквадратичного отклонения, моды, медианы, наибольшего и наименьшего варианта выборки. Нужно применить этот инструмент по отдельности к значениям каждого заданного столбца, т.е. отдельно к значениям X и отдельно к значениям Y.

• Экспоненциальное сглаживание

• Двухвыборочный F-тест для дисперсии

• Анализ Фурье

• Гистограмма

Инструмент «Гистограмма» применяется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений. При этом рассчитываются числа попаданий для заданного диапазона ячеек.

Например, можно получить распределение успеваемости по шкале оценок в группе из 20 студентов. Таблица гистограммы состоит из границ шкалы оценок и групп студентов, уровень успеваемости которых находится между самой нижней границей и текущей границей. Наиболее часто встречающийся уровень является модой диапазона данных.

• Скользящее среднее

• Генерация случайных чисел

• Ранг и персентиль

• Регрессия

• Выборка

• T-тест

• Z-тест