Дәріс. Активті кедергі, идеал индуктивті элемент және сыйымдылық элементтер параллель жалғанған тізбек

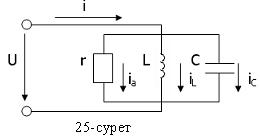Параллель қосылған активті кедергі r, идеал индуктивті элемент Lжәне сыйымдылық элементтен Cтұратын электр тізбегін синусоидалы кернеуге u=U_msinωt қосайық(25-сурет). Барлық тармақтардағы токтарды анықтайық. Кирхгофтың бірінші заңы бойынша:

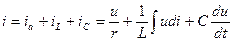, немесе i=(U_m/r)sinωt+(U_m/ωL) sin(ωt-90˚)+ωCU_m sin(ωt+90˚).

Комплекстік әрекеттік мәндерге көшейік:

I=Ie^jφ, I_a= I_ae^j0, I_L=I_Le^-j90˚ , I_C=I_Ce^j90˚ , мұндағы I_a=U/r, I_L=U/ωL,

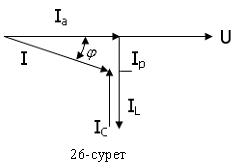
I_C=UωC – токтардың модульдері, ал U=U_m/ 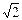. Алынған теңдеуден активті кедергідегі токтың фаза бойынша кернеумен бірдей болатынын көреміз. Ток индуктивті элементте фаза бойынша 90˚ артта қалады, ал ток сыйымдылық элементтегі кернеуден фаза бойынша 90˚ озады. Кернеу мен токтардың векторларының өзара орналасуы 26-суреттегі векторлық диаграммада көрсетілген. Индуктивті ток I_L пен сыйымдылық токтың I_C фазалары қарама-қарсы болғандықтан олар бір бірінен алынады. Олардың айырымын реактивті ток деп атайды: I_p= I_L- I_C. Векторлық диаграммадан активті ток I_a, реактивті ток I_p және тізбектің толық тогы I тікбұрышты үшбұрыш құрайтынын көреміз. Бұл токтар үшбұрышының катеттерін I_a және I_p токтары құрайды да, ал гипотенузасы I тогы болады. Пифагор теоремасы бойынша : , ,

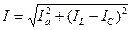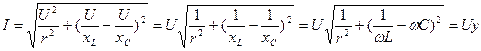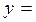
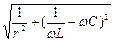
мұндағы 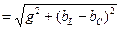– тізбектің толық өткізгіштігі. Бұл өрнектегі g=1/r-активті өткізгіштік деп, b_L=1/x_L=1/ ωL реактивті индуктивтіөткізгіштік деп, ал b_C=1/x_C=1/ ωC реактивті сыйымдылық өткізгіштік деп аталады.

Токтар үшбұрышынан тізбектегі кернеудің U толық токтан I фаза бойынша қаншалықты ығысқандығын табуға болады: 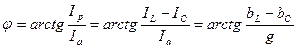. Егер b_L > b_C болса φ таңбасы оң, ал b_L < b_C болғанда таңбасы теріс болады.

Егер толық ток I және φ белгілі болса, онда I_a= Icosφ, I_p= Isinφ.

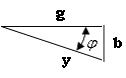27-сурет

Тізбектің толық өткізгіштігінің өрнегі бір катеті активті өткізгіштікке g тең, екінші катеті реактивті өткізгіштікке тең b (b= bL - bC), ал гипотенузасы толық өткізгіштікке y тең тікбұрышты үшбұрышқа сәйкес келеді( 27-сурет). Бұл үшбұрышты өткізгіштер үшбұрышыдеп аталады Ток пен кернеу арасындағы фазалық ығысуды өткізгіштер үшбұрышы арқылы табуға болады: φ=arctg( bL - bC)/g. Бұл өрнектен фазалық ығысу индуктивті және сиымдылық өткізгіштіктердің өзара қарым-қатынасына байланысты екендігі көрінеді.

Егер b >0 болса, онда реактивті өткізгіштік b индуктивті сипатта, ал b_L < 0 сыйымдылық сипатта болады. Егер b = 0 болса, онда тізбекте токтар резонансы болды.

Егер y және φ белгілі болса, онда g= ycos φ, b= ysin φ.

Токтарды да, қуаттарды да өткізгіштіктер арқылы есептеуге болады: активті ток I_a=Ug, реактивті индуктивті ток I_L=Ub_L,, реактивті сыйымдылық ток I_C= Ub_C , ал тізбектің реактивті тогы I_p= Ub, толық ток I=U y.

Тізбекте бөлінетін активті қуат P=U²g, реактивті индуктивті қуат Q_L=U² b_L,, реактивті сыйымдылық қуат Q_C= U² b_C,, толық қуат S= U² y.

Негізгі әдебиеттер: [1(86-91), 3(167-171)]

Қосымша әдебиеттер: [ 5,6,7,8]

Бақылау сұрақтары:

1.Параллель қосылған активті кедергі r, идеал индуктивті элемент Lжәне сыйымдылық элементтен Cтұратын электр тізбек күйінің теңдеуі. Активті, реактивті және толық токтар.

2. Векторлық диаграмма. Токтар үшбұрышы.

3.Тізбектің активті, реактивті және толық өткізгіштіктері. Өткізгіштіктер үшбұрышы.

4.Фазалық ығысу. Тізбектегі энергетикалық үрдістер.Активті, реактивті және толық қуаттар.