Дәріс. Периодтық синусоидалы емес тоқ тізбектері

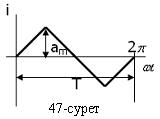Синусоидалы емес ток немесе кернеу деп уақытқа тәуелді синусоидалы емес заңдылықпен өзгеретін ток пен кернеуді айтады. Тізбекте синусоидалы емес ток немесе кернеу қоректендіргіш синусоидалы емес э.қ.к. өндіретін болса немесе тізбектің элементтерінің кем дегенде біреуі сызықты емес болса, немесе олар уеқытқа тәуелді периодты түрде өзгерген жағдайларда пайда болады. Синусоидалы емес токтар немесе кернеулер периодты қисықтар немесе периодты емес қисықтар арқылы сипатталады. Біз периодты синусоидалы емес токтар немесе кернеулер ( 47-сурет) тізбегін қарастырамыз. Сызықты тізбекке периодты синусоидалы емес э.қ.к, ток немесе кернеу әсер еткен кезде болатын құбылыстарды зерттеу жұмыстарын жеңілдету мақсатында синусоидалы емес э.қ.к-тің, токтың немесе кернеудің қисықтарын Фурье қатарларына жіктеу тиімді.

Егер период 2π-ге тең болса, онда кез келген синусоидалық емес шамаларды Фурье қатарына жіктеу арқылы өрнектеуге болады.

Жалпы жағдайда ,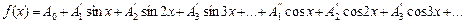

мұндағы 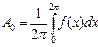- тұрақты құрамдас бөлік; 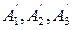,..., 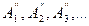-синусоидалық және косинусоидалық гармоникалардың амплитудалары.

Математикадан: 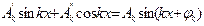, мұндағы

, .

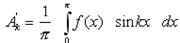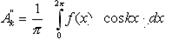Бұл формуланы пайдаланып Фурье қатарын жазамыз:

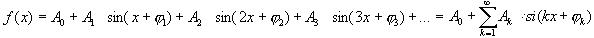
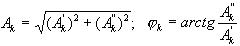
Сонымен периоды 2 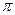-ге тең синусоидалы емес шамаларды тұрақты мүшесі бар және синусоидалық гармоникалардың жиынтығының қосындылары ретінде көрсетуге болады.

Симметриялы, периодты қисық сизықтардың қасиеттері.1)Абцисса өсіне симметриялы қисық сызықтар үшін 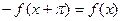. Мұндай қисық сызықтардың өрнектеріде тұрақты мүше мен жұп гармоникалар болмайды: A₀=A₂=A₄=A₆=0; ;

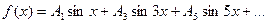2) Ордината осіне симметриялы қисық сызықтар үшін 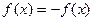. Бұл кезде синусоидалы гармоника болмайды: ; ;

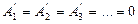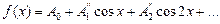3) Координата басына симметриялы қисық сызық үшін 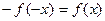. Өрнектерде тұрақты мүше және косинусоидалы гармоника болмайды, яғниА₀=0, ;

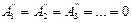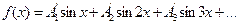
Фурье қатарындағы коэффициеттерін графикалық тәсілмен табу.Бұл тәсіл анықталған интегралды шекті санды қосылғыштар қосындысымен ауыстыруға негізделген. Егер f(ωt)-функциясы аналитикалық емес, графикалық түрде берілсе, онда А₀ ,А′_км және А″_км- коэффициенттерін мына өрнектер бойынша анықтайды:

;

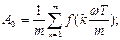
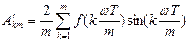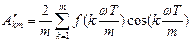
мұндағы т- периодтық синусоидалық емес функцияны бірдей кесінділерге бөлгендегі сан. Коэффициенттерді есептеу үшін Т-периоды т бірдей интервалға бөлінеді және сол т бөліну нүктелеріндегі қисықтың 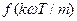-ординаталары анықталады, мұндағы к=1,2,3...m.

Ара тәріздес қисықты функция үшін : .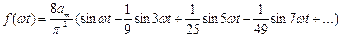

Синусоидалы емес шамалардың әрекеттік мәндері.Токтың әрекеттік мәні: .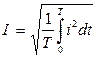

Мұндағы

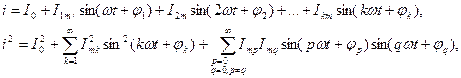
Екінші қосылғыштың интегралы 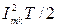, ал үшінші қосылғыштың интегралы нөлге тең болады. Сонда 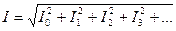, сол сияқты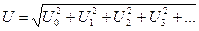

Сонымен әрекеттік мән тұрақты мүшенің квадратына мен гармоникалардың әрекеттік мәндерінің квадратының қосындыларының квадрат түбірі ретінде табылады.

Синусоидалы емес шамалардың модульдарының орташа мәнідеп бұл функцияның период ішіндегі модулінің орташа мәнін айтады:

,

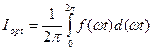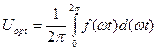
Егер f(ωt) абцисса өсіне қатысты симметриялы болса және жарты период ішінде f(ωt) функциясы өзінің таңбасын өзгертпесе, онда модуль бойынша орташа мән жарты периодтағы орташа мәнге тең.

Синусоидалы емес ток тізбегіндегі активті және толық қуаттар. Синусоидалы емес токтың активті қуаты бір период ішіндегі орташа қуат ретінде анықталады:

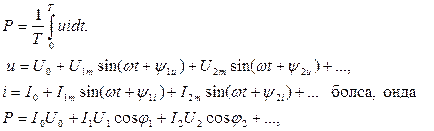
мұндағы U₁, U₂,…-кернеулердің гармоникаларының әрекеттік мәндері;I₁, I₂, I₃…- токтардың гармоникаларының әрекеттік мәндері; 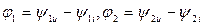- кернеу мен тоқтың гармоникаларының фазалық айырымы. Сонымен активті, реактивті және толық қуаттар:

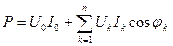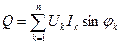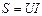; ; , мұндағы U ,I- синусоидалы емес кернеу мен токтың әректтік мәндері. Әдетте, синусоидалы емес токтар үшін S² ≥P² +Q² .

Синусоидалы емес ток тізбегін есептеу. Егер сызықты тізбекке периодты синусоидалы емес кернеу әсер етсе, онда есептеу үш кезеңге бөлінеді: 1) периодты синусоидалы емес э.қ.к. немесе токтарды тұрақты және синусоидалы құраушыларға жіктеу; 2) беттестіру принципін пайдаланып тізбектегі токтар мен кернеулерді әрбір құраушы үшін жеке-жеке есептеу. 3) әрбір жеке құраушылары үшін алынған мәндерді біріктіріп қарастыру.

Синусоидалық емес функцияны сипаттау үшін мынадай коэффициенттер қолданылады:

- амплитудалық коэффициент K_a =A_m/A, мұндағы A_m- функцияның максимал мәні, A- әрекеттік мән;

- пішіндік коэффициент K_п =A/A_орт , мұндағы A_орт - функцияның орташа мәні;

- бұрмалану коэффициенті K_б =A₁/A, А₁- функцияның бірінші гармоникасының әрекеттік мәні.

Негізгі әдебиеттер: [2(4-35), 3(455-497)]

Қосымша әдебиеттер: [ 5,6,7,8]

Бақылау сұрақтары:

1. Синусоидалы емес ток немесе кернеуге түсініктеме беріңіз

2. Периодты синусоидалы емес шаманы Фурье қатарына жіктеу қалай жүргізіледі?

3. Симметриялы, периодты қисық сизықтардың қандай қасиеттері бар?