Дәріс. Синусоидалы ток тізбегін есептеудің комплекстік тәсілі.
 Комплекстік тәсіл лездік мәндер үшін құрылатын дифференциалдық теңдеуден комплекстік мәндер үшін құрылатын алгебралық теңдеуге өткізуге мүмкіндік береді. Комплекстік тәсілді пайдаланған кезде синусоидалық шамаларды комплекстік сандар ретінде көрсетеді:
Комплекстік тәсіл лездік мәндер үшін құрылатын дифференциалдық теңдеуден комплекстік мәндер үшін құрылатын алгебралық теңдеуге өткізуге мүмкіндік береді. Комплекстік тәсілді пайдаланған кезде синусоидалық шамаларды комплекстік сандар ретінде көрсетеді:
А 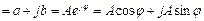 , мұндағы
, мұндағы 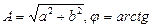 b/a.
b/a.
Егер 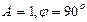 , онда
, онда 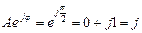 . Егер
. Егер 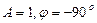 , онда
, онда 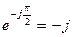
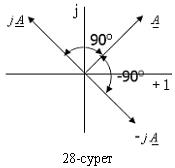
 Кез-келген векторды
Кез-келген векторды 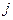 -ға көбейткенде, ол вектордың модулін өзгертпей 90о-қа бұрады.,ал -
-ға көбейткенде, ол вектордың модулін өзгертпей 90о-қа бұрады.,ал - 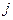 -ға көбейткенде векторды - 90о-қа бұрады ( 28-сурет). Комплекстік тәсілді пайдалану арқылы синусоидалы шамалардың лездік мәндерін анықтайтын дифференциалдық теңдеулерден комплекстік мәндер арқылы өрнектелген алгебралық теңдеулерге көшуге болады. Бұл есептеу жұмысын жеңілдетуге мүмкіндік береді. Комплекстік тәсілді пайдаланған кезде токтың лездік мәнін (i) оның комплекстік амплитудалық мәніне ( I m) айырбастаймыз, ал лездік активті кернеуді ua=ir комплекстік активті кернеумен. Im r, лездік индуктивті кернеуді uL=L di/dt комплекстік индуктивті кернеумен Im jωL , ал лездік сыйымдылық кернеуді uC=(1/C) ∫idt комплекстік сыйымдылық кернеумен Im(-j/ωC), лездік э.қ.к.-ті e комплекстік кернеумен Em айырбастаймыз.
-ға көбейткенде векторды - 90о-қа бұрады ( 28-сурет). Комплекстік тәсілді пайдалану арқылы синусоидалы шамалардың лездік мәндерін анықтайтын дифференциалдық теңдеулерден комплекстік мәндер арқылы өрнектелген алгебралық теңдеулерге көшуге болады. Бұл есептеу жұмысын жеңілдетуге мүмкіндік береді. Комплекстік тәсілді пайдаланған кезде токтың лездік мәнін (i) оның комплекстік амплитудалық мәніне ( I m) айырбастаймыз, ал лездік активті кернеуді ua=ir комплекстік активті кернеумен. Im r, лездік индуктивті кернеуді uL=L di/dt комплекстік индуктивті кернеумен Im jωL , ал лездік сыйымдылық кернеуді uC=(1/C) ∫idt комплекстік сыйымдылық кернеумен Im(-j/ωC), лездік э.қ.к.-ті e комплекстік кернеумен Em айырбастаймыз.
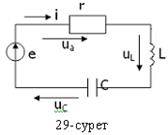
29-суретте көрсетілген тізбекке Кирхгофтың екінші заңы бойынша лездік мәндер үшін теңдеу құрайық: ua+ uL+ uC= e, немесе
Im r 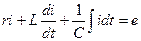
Теңдеуді комплекстік түрде жазайық: Im r + Im jωL - Im(j/ωC) = Em, Im [ r + j( ωL --1/ωC)] = Em ,
бұдан Im = Em / [ r +j ( ωL --1/ωC)]= Em /Z .
Бұл теңдеудің оң жағын да, сол жағын да √2 бөлсек, онда комплекстік әрекеттік мәндер үшін Ом заңын аламыз: I =E /Z .Мұндағы Z– тізбектің комплекстік кедергісі: Z=[ r +j( ωL --1/ωC)]= r+jx = zej φ. Комплекстік кедергінің нақты бөлігі активті кедергіге r, ал жорамал бөлігі реактивті кедергіге x = ( ωL --1/ωC) тең. Комплекстік кедергінің модулі 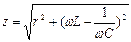 .
.
Комплекстік өткізгіштікдеп комплекстік кедергіге кері шаманы айтады:
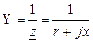 ,
, 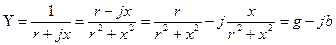
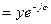 , мұндағы
, мұндағы 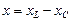 ,
,
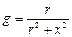 - активті өткізгіштік,
- активті өткізгіштік, 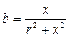 - реактивті өткізгіштік,
- реактивті өткізгіштік, 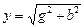 - толық өткізгіштік.
- толық өткізгіштік.
Ом заңын комплекстік өткізгіштік арқылы жазайық: I =UY, I =Ug – U b= Ia + Ip.
Сонымен электр тізбегінің толық өткізгіштігі нақты бөлігі активті өткізгіштікке, ал жорамал бөлігі реактивті өткізгіштікке тең комплекс сан ретінде жазылады.
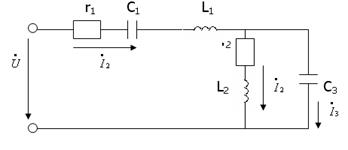 30-сурет
30-сурет
| 30-суретте көрсетілген тізбектің тармақтарының комплекстік кедергілерін жазайық. Ол үшін алдымен активті және реактивті кедергілердің комплекстік түрде жазылуын көрсетейік: 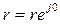 = r, XL = r, XL 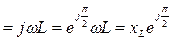 , . , .
|
XC 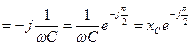
Тізбектің тармақтарының комплекстік кедергілері:
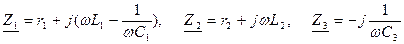
Тізбектің толық комплекстік кедергісі: 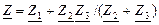
Комплекстік қуат деп кернеудің комплекстік әрекеттік мәнін түйіндес токтың комплекстік әрекеттік мәніне көбейткенге тең: 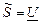 Ỉ. Берілген комплекстік токқатүйіндестоктыңмодулі осы токтың модулімен бірдей, ал фазасы қарама-қарсы болып келетін токтыайтады.Айталық,
Ỉ. Берілген комплекстік токқатүйіндестоктыңмодулі осы токтың модулімен бірдей, ал фазасы қарама-қарсы болып келетін токтыайтады.Айталық, 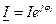 - берілген ток болса, онда түйіндес ток Ỉ
- берілген ток болса, онда түйіндес ток Ỉ 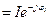 .
.
Егер 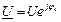 болған жағдайда
болған жағдайда 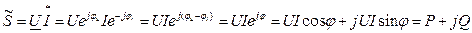 , мұндағы
, мұндағы
P = UIcosφ - активті қуат; 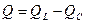 = UIsinφ - реактивті қуат. Бұдан комплекстік қуаттың нақты бөлігі активті қуатқа тең, ал жорамал бөлігі реактивті қуатқа тең.
= UIsinφ - реактивті қуат. Бұдан комплекстік қуаттың нақты бөлігі активті қуатқа тең, ал жорамал бөлігі реактивті қуатқа тең.
Комплекстік қуаттың көрсеткіш түрде жазылуы: 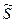 =sejφ, мұндағы
=sejφ, мұндағы 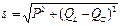 ,
, 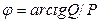 .
.
Синусоидалы ток тізбегіндегі қуаттар тепе-теңдігімынаны білдіреді: біріншіден, тізбектегі барлық қоректендіргіштердің активті қуаттарының алгебралық қосындысы сол тізбектегі резистивті элементтердің активті қуаттарының арифметикалық қуаттарының қосындысына тең:
∑UқорIқор cos(φu – φi)= ∑rIr 2 немесе ∑Pқор = ∑Pr ,
екіншіден, тізбектегі барлық қоректендіргіштердің реактивті қуаттарының алгебралық қосындысы сол тізбектегі индуктивті элементтердің реактивті қуаттарының арифметикалық қосындысы мен сыйымдылық элементтердің реактивті қуаттарының арифметикалық қосындысының айырмасына тең: ∑UқорIқор sin(φu – φi)= ∑xLI2 L -∑ xCI2 C , немесе ∑Qқор =∑QL - ∑QC.
Қоректендіргіштердің активті және реактивті қуаттарының алгебралық қосындысының қосылғыштарының таңбасы токтың оң бағыты э.қ.к.-тің бағытымен сәйкес болған жағдайда плюс болады, егер, ал керісінше жағдайда минус болады. Қуаттар тепе-теңдігін комплекс түрде өрнектеуге болады: ∑ 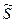 қор =∑
қор =∑ 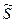 қаб, немесе ∑
қаб, немесе ∑ 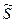 қор =∑Uқор Ỉқор = ∑Pқор +j∑Qқор , ∑
қор =∑Uқор Ỉқор = ∑Pқор +j∑Qқор , ∑ 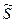 қаб =∑Uқаб Ỉқаб= ∑Pқаб +j∑Qқаб. Сондықтан ∑Pқор = ∑Pқаб, ∑Qқор = ∑Qқаб.
қаб =∑Uқаб Ỉқаб= ∑Pқаб +j∑Qқаб. Сондықтан ∑Pқор = ∑Pқаб, ∑Qқор = ∑Qқаб.
Топографиялық диаграммадаоның белгілі бір нүктесіне тізбек сұлбасының белгілі бір нүктесінің комплекстік потенциалы сәйкес келеді. Потенциалы нөлге тең деп алынған сұлба нүктесі координаталар басына тура келеді. Топографиялық диаграмма тізбектің кез-келген нүктелерінің арасындағы кернеуді оңай анықтауға мүмкіндік береді. Ол үшін диаграммадағы тиісті нүктелерді түзумен қосады.
Негізгі әдебиеттер: [1(83-91, 97-102), 3(172-209)]
Қосымша әдебиеттер: [5,6,7,8]
Бақылау сұрақтары:
1.Синусоидалы токтың комплекстік мәндері үшін Ом және Кирхгоф заңдары.
2.Комплекстік кедергі. Комплекстік өткізгіштік.
3.Комплекстік қуат. Қуаттар тепе –теңдігі. Қуатты ваттметрмен өлшеу.
4. Топографиялық диаграммаға түсініктеме беріңіз.
Дата добавления: 2015-09-11; просмотров: 5919;
