Дәріс. Индуктивті байланысқан элементтері бар тізбектер

Тізбектің бір контурында немесе бір элементінде ток өзгерген кезде басқа контурда немесе басқа элементте э.қ.к. пайда болса, онда осы екі контурды немесе екі элементті бір-бірімен индуктивті байланысқан (магнитті байланысқан) дейді, ал екінші контурда немесе екінші элементте пайда болған э.қ.к.-ті өзаралық индукцияның э.қ.к.-і деп атайды.

Өзара қатар ораласқан, орам сандардары w₁ және w₂ тең екі индуктивтілік орамалармен i₁ және i ₂ токтары жүрсе, онда әр ораманың барлық магнит сызықтары екінші ораманың орамдарымен ілінісуі мүмкін, яғни Ф₂₁ =Ф₁₁, Ф₁₂ =Ф₂₂. Сондықтан мұндай тізбектерді талдау кезінде орамалардың өздерінің ағын ілінісулерінен ( Ψ₁₁ және Ψ₂₂) басқа қосымша ағын ілінісулерін ( Ψ₁₂ және Ψ₂₁) есепке алу керек. Бірінші ораманың өзіндік ағын ілінісуі Ψ₁₁=Ф₁₁ w₁=L₁ i₁, бірінші ораманың тогының әсерінен пайда болған екінші орамадағы қосымша ағын ілінісуі Ψ₂₁= Ф₂₁ w₂=Ф₁₁ w₂=М₂₁ i₁ , мұндағы М₂₁= Ψ₂₁/i₁ –пропорциональдық коэффициент, өзаралық индуктивтілік деп аталады. Бұл өрнектерден

L₁/ М₂₁= w₁/ w₂.

Екінші ораманың өзіндік ағын ілінісуі Ψ₂₂=Ф₂₂ w₂=L₂ i₂, екінші ораманың тогының әсерінен пайда болған бірінші орамадағы қосымша ағын ілінісуі Ψ₁₂= Ф₁₂ w₁=Ф₂₂ w₁=М₁₂ i₂ . Бұл өрнектерден L₂/ М₁₂= w₂/ w₁. Көрсетілген екі қатынастан М₁₂ М₂₁= L₁L₂ екендігін көруге болады. Тәжірибе М₁₂ = М₂₁=М екендігін көрсетеді. Демек, өзаралықиндуктивтілік М= .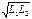

Егер бір ораманың магнит сызықтарының тек біраз бөлігі ғана екінші орамамен ілініссе, яғни Ф₂₁ <Ф₁₁, Ф₁₂ <Ф₂₂ болса, онда өзаралықиндуктивтілік М=К 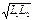, мұндағы К= М / 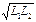- байланыс коэффиценті деп аталады. Бұл коэффициенттің мәні бірден кіші К<1, өйткені Ф₂₁ <Ф₁₁, Ф₁₂ <Ф₂₂, яғни бір ораманың магнит ағыны екінші ораманы толық қамтымайды.

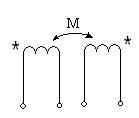
­Өзаралықиндуктивтілік токтардың мәндері мен бағыттарына тәуелді емес , ол орамалардың құрылысымен және өзара орналасуымен анықталады. Қарастырылған екі ораманың толық ағын ілінісуі Ψ екі құраушыдан тұрады. Құраушылар токтардың бағыттарына және өзара орналасуына байланысты қосылуы немесе бірі бірінен алынуы мүмкін. Сұлбада орамалардың аттас ұштарын ( қысқыштарын) нүктелер арқылы белгілейді (35-сурет). Егер токтар бағыттары орамалардың аттас ұштарына байланысты бірдей болса, онда орамалар өзара үйлесімді қосылған (35а-сурет). Бұл жағдайда бірінші ораманың толық ағын ілінісуіΨ₁= Ψ₁₁+ Ψ₁₂, ал екінші ораманың толық ағын ілінісуі Ψ₂= Ψ₂₂+ Ψ₂₁.Егер токтар бағыттары орамалардың аттас ұштарына байланысты бірдей болмаса, онда орамалар өзара қарсы қосылған (35ә-сурет). Бұл кезде бірінші ораманың толық ағын ілінісуі Ψ₁= Ψ₁₁ - Ψ₁₂, ал екінші ораманың толық ағын ілінісуі Ψ₂= Ψ₂₂ - Ψ₂₁.

Өзаралық индукцияның э.қ.к.-і.Егер өзаралық ағын ілінісуі уақытқа тәуелді өзгерсе, онда орамаларда өзаралық индукцияның э.қ.к.-тері пайда болады: е_2м= -dΨ₂₁ /dt , немесе е_2м= -Mdi₁/dt, ал бірінші орамада е_1м= -dΨ₁₂ /dt, немесе е_1м=- Mdi₂/dt. Екінші орамада пайда болған өзіндік индукция э.қ.к.-і бірінші орамадағы токтың өзгерісіне қарсы әсер етеді.

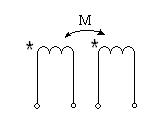а) б) 35-сурет а) ә) б) 36-сурет

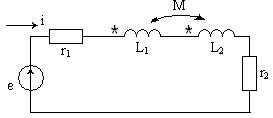
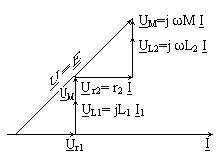
Индуктивті байланысқан элементтер бірізді жалғанған тізбек(36а-сурет).Тізбек бірізді қосылған r1 мен r2 активті кедергілерден және L1 мен L2 индуктивтіліктен құралсын. Индуктивті элементтер арасындағы магниттік байланысты өзара индуктивтілік М сипаттайды. Оларды тізбекке қосудың екі сұлбасы болуы мүмкін. Индуктивтілік орамаларды үйлесімді қосқан кезде олардың аттас ұштарымен салыстырғанда тізбектегі ток бір бағытта жүреді. Сондықтан әр индуктивті элементпен ілінісетін өзіндік индукцияның және өзара индукцияның магнит ағындары қосылады. 36а–суретте көрсетілген тізбек үшін Кирхгоф екінші заңы бойынша теңдеу құрайық. Егер токтар бағыттары орамалардың аттас ұштарына байланысты бірдей болмаса, онда орамалар өзара қарсы қосылған. Бұл жағдайда бірінші ораманың толық ағын ілінісуі Ψ1= Ψ11 - Ψ12, ал екінші ораманың толық ағын ілінісуі Ψ2= Ψ22 - Ψ21. Ir1+L1 di/dt + M di/dt+L2 di/dt+ M di/dt+ir2 =e. Комплекстік түрде: I[r1+r2+jω(L1+L2+2M)]=E. Бұдан орамалар үйлесімді қосылған кездегі олардың толық индуктивтілігін анықтаймыз: Lүйл =L1+L2+2M. Тізбектің толық кедергісі Zүйл=r1+r2+jω(L1+L2+2M)=Z1+Z2+2Zm, мұндағы Z1=r1+ jωL1, Z2= r2+jωL2,, Zm= jωM.-орамалардың комплекстік кедергілері және өзара индукцияның комплекстік кедергісі. Орамалар үйлесімді қосылған жағдайға сәйкес келетін векторлық диаграма 36ә–суретте көрсетілген. Орамаларды қарсы қосқан кезде олардың аттас ұштарымен салыстырғанда тізбектегі ток қарама-қарсы бағытта жүреді. Сондықтан әр индуктивті элементпен ілінісетін өзіндік индукцияның және өзара индукцияның магнит ағындары бір-біріне қарсы бағытталады, яғни толық магнит ағыны азаяды. Бұл жағдайда Кирхгофтың екінші заңы

бойынша құрылған теңдеу:

Ir₁+L₁ di/dt - M di/dt+L₂ di/dt- M di/dt+ir₂ =e.

Комплекстік түрде: I[r₁+r₂+jω(L₁+L₂ -2M)]=E

Орамалар қарсы қосылған кездегі олардың толық индуктивтілігін анықтаймыз: L_қар =L₁+L₂ -2M. Тізбектің толық кедергісі Z_қар= r₁+r₂+jω(L₁+L₂ -2M)=Z₁+Z₂ - 2Z_m,

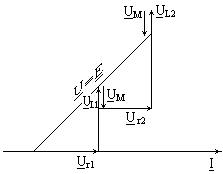
36б -суретте орамалардың қарсы қосылған сұлбасына сәйкес келетін векторлық диаграмма көрсетілген.

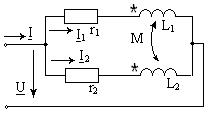
Индуктивті байланысқан элементтер параллель жалғанған тізбек.Өзара индуктивтігі М, кедергілері r₁ мен r₂ , ал индуктивтері L₁ мен L₂ болатын екі қабылдағыш параллель қосылған.

37-сурет

Орамалардың аттас ұштары бір түйінге қосылған (37 -сурет). Токтар мен кернеулердің таңдап алынған оң бағытында I=I1+I2; U=Z1I1+Zm I2; U=ZmI1+Z2 I2, ,мұндағы Z1=r1+ jωL1,, Z2=r2+jωL2,, Zm=jωM. Бұл теңдеулерді шешкенде ; ; ;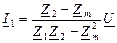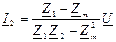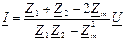

Бұдан тізбектің комплекстік кедергісі .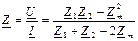

Тізбектің толық индуктивтігі L_үйл 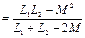. Тармақтар арасында индуктивтік байланыс болмаған жағдайда, яғни Z_m=0 болғанда, бұл өрнек мына түрге келеді: .

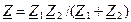Егер орамалардың аттас ұштары әр түйінге қосылған болса, яғни орамалар қарсы қосылған жағдайда, кернеудің теңдеуіндегі Z_m таңбасы минусқа өзгереді. Демек, бұл жағдайда тізбектің кірістік комплекстік кедергісі 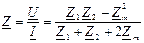, ал толық индуктивтілігі L_қар .

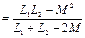Индуктивті байланысқан элементтер бар күрделі тізбекті есептеу.Мұндай тізбектерді есептеу үшін Кирхгоф екінші заңы бойынша теңдеулер құрған кезде, индуктивті орамалар үшін жазылатын кернеулердің өрнегіне өзара индукцияның комплекстік кернеуін 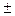jωMI қосу керек. Егер орамалар үйлесімді қосылса, онда бұл комплекс оң таңбалы, ал қарсы қосылған жағдайда теріс таңбалы болады.

Индуктивті байланысқан элементтері бар тізбекті индуктивті байланысы жоқ балама сұлбамен ауыстыруарқылы тізбекті есептеуді жеңілдетуге болады. Екі элементтен (Z₁ және Z₂) тұратын индуктивті байланысы бар тізбекті балама сұлбамен ауыстырғанда Z₁ мен Z₂ кедергілеріне 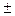Z_м кедергісі жалғанады және олар мен жаңа пайда болған түйін арасына 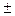Z_м кедергісі қосылады. Егер индуктивті байланысқан үш элементтер үш сәулелі жұлдызша немесе ұшбұрыш арқылы жалғанған болса , онда жоғарыда келтірілген тәсіл бойынша индуктивті байланыстан құтылып, оған балама сұлбаға көшуге болады.

Темір өзекшесіз трансформатор (ауа трансформаторы). Трансформатор деп тізбектегі энергияны басқа тізбекке электромагниттік индукция құбылысы арқылы беретін аппаратты айтады.

Оның қарапайым түрі ферромагниттік өзекшесіз индуктивті байланысқан екі орамадан тұрады. Кернеу көзі бірінші орамаға қосылады, ал жүктеме екінші орамаға қосылған.

Трансформатордың теңдеулері мына түрде жазылады:

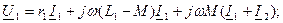
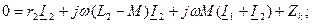
Мұндағы r₁ , L₁ және r₂ , L₂ – бірінші және екінші орамалардың активті кедергілері және индуктивтері; Z _қ =r_қ +jX_қ –жүктеменің кедергісі; I₁, I₂ – бірінші және екінші орамадағы токтар.

Екінші орамадағы ток: I₂ =-jX_m I₁ /( r_2қ +jX_2қ ). Токты трансформациялау коэффициенті: k_i=I₂ /I₁ =X_m /z_2қ . Кернеуді трансформациялау коэффициенті: k_u =U₂ / U₁ . Егер L₁ <M<L₂ болса,онда L₁ -M теріс, яғни сиымдылық сипатта болады. Бұл жағдайда U₂ >U₁ , демек, трансформатор кернеуді жоғарлатады. Егер L₁ >M>L₂ болса,онда L₂ -M теріс, яғни сиымдылық сипатта болады. Бұл жағдайда U₂ <U₁ , демек, трансформатор кернеуді төмендетеді.

Негізгі әдебиеттер: [1(124-144), 3(278-302)]

Қосымша әдебиеттер: [ 5,6,7,8]

Бақылау сұрақтары:

1.Тізбектің индуктивті байланыстағы элементтері жөнінде түсініктеме беріңіз. Байланыс коэффициенті қалай анықталады?

2. Өзара индукцияның э.қ.к.-і дегеніміз не? Орамалардың өзара үйлесімді және қарсы қосылуы туралы түсініктеме беріңіз.

3. Индуктивті байланысқан элементтері бірізді жалғанған тізбекті есептеу жұмысы қалай жүргізіледі? Векторлық диаграммасына түсініктеме беріңіз

4. Индуктивті байланысқан элементтері параллель жалғанған тізбекті есептеу жұмысы қалай жүргізіледі? Векторлық диаграммасына түсініктеме беріңіз

5.Темір өзекшесіз трансформатор (ауа трансформаторы туралы түсініктеме беріңіз.

№12 Дәріс. Үш фазалы қоректендіргіштер және үш фазалы тізбектер туралы түсініктемелер. Қоректендіргіш пен қабылдағыштың фазалары жұлдызша сұлбасы бойынша жалғанған үш фазалы тізбек

Электр тізбегінің көп фазалы жүйесі деп жиіліктері бірдей, ал фаза бойынша бірі бірінен ығысқан бірнеше айнымалы э.қ.к-тер тізбектерінің жиынтығын айтады. Көбінесе практикада амплитудалары тең және фазалары бойынша 2π/т – бұрышқа ығысқан ( мұндағы т-фаза саны) бірнеше э.қ.к.-терден тұратын көп фазалық симметриялықжүйелер қолданылады. Қазіргі кезде көп фазалық жүйелердің ішінде ең көп тарағаны -үш фазалы жүйелер.

Үш фазалы симметриялы э.қ.к.-тер жүйесі деп бірдей жиілікті және бірдей амплитудалы, ал фаза бойынша 120⁰ ығысқан үш синусоидалы э.қ.к.-тердің жиынтығын айтады.

Үш фазалы симметриялы э.қ.к.-тер жүйесін алу үшін үш фазалы синхронды генератор қолданылады. Оның статорында бірі бірінен 120⁰-қа ығысқан және өзара оқшауланған үш фазалық орама орналасқан. Ротор айналғанда осы орамаларда амплитудалары бірдей, жиіліктері бірдей, бірақ фаза бойынша 120⁰- қа ығысқан үш э.қ.к.-тер пайда болады. Олардың біреуін е_А (Е_А ), одан фаза бойынша 120⁰ кеш қалған екіншісін е_В (Е_В), ал біріншіден фаза бойынша 120⁰ озған э.қ.к.-і е_С (Е_С) белгілейміз.

Генератордың орамаларын оның фазалары деп атайды да, А,В,С латын әріптері арқылы белгілейді. Фазалар кезектесуі деп э.қ.к.-тердің белгілі бір мәнге ие болу кезіндегі ретін айтады . Егер бұл рет Е_А , Е_В , Е_С болса, онда мұндай кезектесу тура кезектесу деп аталады.

Симметриялы генератордың фазалық орамаларының э.қ.к.-тердің лездік мәндері:

е_А =Е_тsinωt, е_В =E_msin(ωt-120⁰), е_С=E_msin(ωt+120⁰).

Э.қ.к.-тердің комплекстік әрекеттік мәндері: Е_А =Е_фе^j0˚, E_B= Е_фе ^-j120˚, E_C= Е_фе ^j120˚ .

Э.қ.к.-тердің комплекстік әрекеттік мәндерінің алгебралық қосындысы нөлге тең және э.қ.к.-тердің лездік мәндерінің алгебралық қосындысы да нөлге тең: Е_А+E_B+E_C=0; е_А+ е_В+ е_С =0.

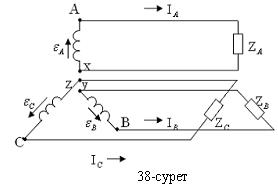Үш фазалы тізбек деп үш фазалы э.қ.к.-тер жүйесі мен үш фазалы қабылдағыштың ( жүктеменің) және жалғау сымдарының жиынтығын айтады. Үш фазалы тізбектің фазасы деп оның бойымен белгілі бір ток ғана жүретін бөлігін айтады. Үш фазалы жүйе алу үшін генератордың мен жүктеменің фазаларын өзара әр түрлі сұлба бойынша қосады:

1.Алты сым арқылы жалғану сұлбасы (38-сурет). А, В,С- генератор орамаларының басқы ұштары; x,y,z- орамалардың аяққы ұштары;

Бұл сұлба бойынша генератордың әр фазасы жүктеменің әр фазасымен екі сым арқылы жалғанады. Барлығы алты сым керек болады.. Бұл сұлба экономикалық жағынан тиімсіз.

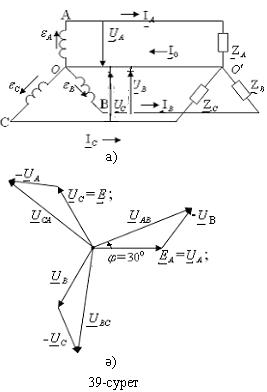2.Жұлдызша сұлба бойынша жалғағанда ораманың аяққы ұштары x,y,z бір нүктеге ( түйінге) қосылады және ол нүктені үш фазалы қоректендіргіштің нөлдік нүктесі немесе бейтарап нүктесі ( О) деп атаймыз(39а-сурет). Сол сияқты жүктеменің де фазаларының бір ұштары бір нүктеге ( түйінге) қосылады және ол нүктені жүктеменің нөлдік нүктесі немесе бейтарап нүктесі ( О′) деп атаймыз. Генератордың орамаларының басқы ұштарын жүктемемен қосатын сымдарды желілік сымдар деп атайды, ал олар арқылы жүретін токтар желілік токтар I_A , I_B, I_C деп аталады. Бұл токтар генератордан жүктемеге қарай бағытталған. Генератордыңбейтарап нүктесін жүктеменің бейтарап нүктесімен жалғайтын сымды нөлдікнемесе бейтарапсым деп аталады.Бейтарап сыммен жүретін ток нөлдік ток(I₀) немесе бейтарап ток деп аталады және ол жүктемеден генераторға карай бағытталады.

Үш фазалық жүйеде генератордың фазалық орамаларының ұштарының арасындағы немесе жүктеменің фазаларының ұштарының арасындағы кернеулерді (U_A, U_B ,U_C ) фазалық кернеулер деп аталады. Бұл кернеулерді желілік сымдар мен нөлдік сым арасындағы кернеулердеп де қарастыруға болады. Симметриялы жүйеде фазалық кернеулердің әрекеттік мәндері бірдей болады: U_A =U_B=U_C= U_ф.

Фазалық токтардеп генератордың фазалық орамалары немесе жүктеменің фазалары арқылы жүретін токты айтады.

Желілік кернеулер (U_AB, U_BC ,U_CA ) деп желілік сымдар арасындағы кернеулерді айтамыз. Желілік кернеулерді фазалардың бастапқы ұштарының арасындағы кернеулер деп де қарастыруға болады. Симметриялы жүйеде желілік кернеулердің әрекеттік мәндері бірдей болады: U_AB = U_BC = U_CA = U_ж .

Егер U_A = Е_А, U_B = E_B , U_C = E_C ескерсек, онда желілік кернеулердің комплекстік мәндері: U_AB = Е_А - E_B = U_A - U_B = U_ж e^j30˚ , U_BC= E_B- E_C= U_B- U_C = U_ж e ^–j90˚ , U_CA= E_C- E_A= U_C- U_A = U_ж e ^j150˚ .

Үш фазалы симметриялы қоректендіргіштің фазалары жұлдызша жалғанған кезде фазалық және желілік кернеулер үшін векторлық диаграмма 39ә – суретте көрсетілген. Бұл диаграммадан фазалық және желілік кернеулердің комплекстік мәндері үш бірдей теңбүйірлі үшбұрыш құрайтындығын көреміз. Бұл үшбұрыштан желілік және фазалық кернеулердің әрекеттік мәндері өзара мынадай қатынаста болатындығын көреміз: U_ж =2U_Фcos30˚= .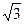

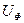Қоректендіргіш пен қабылдағыштың ( жүктеменің) фазаларының токтары: I=E_A/Z_A =U_A/ Z_A, I_B= E_B/Z_B= U_B/ Z_B, I_C= E_C/Z_C= U_C/ Z_C. Бейтарап сымдағы ток I₀ = I_A + I_B + I_C. Қоректендіргіш пен қабылдағыштың ( жүктеменің) фазалары жұлдызша сұлба бойынша жалғанса, желілік токтар оларға сәйкес фазалық токтарға тең болады.

Егер жүктеме симметриялы болса, яғни оның фазаларының кедергілері бір біріне тең болса (Z_A= Z_B = Z_C) болса, онда 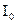=0, яғни нөлдік сыммен ток жүрмейді. Бұл жағдайда нөлдік сымды сұлбадан алып тастауға болады және желілік пен фазалық токтардың әрекеттік мәндері тең: I_Ж=I_Ф.

Негізгі әдебиеттер: [1(156-168), 3(378-393)]

Қосымша әдебиеттер: [ 5,6,7,8]

Бақылау сұрақтары:

1. Үш фазалы симметриялы э.қ.к.-тер жүйесі туралы түсініктеме беріңіз.

2. Желілік және нөлдік (бейтарап) сымдар, желілік және фазалық кернеулер мен токтардың анықтамасына тоқталыңыз.

3. .Қоректендіргіш пен қабылдағыштың фазаларының жұлдызша сұлбасы бойынша жалғануын қарастырып, векторлық диаграмманы тұрғызыңыз. Бейтарап сымның қызметіне тоқталыңыз.

4 Үш фазалық симметриялы жүйедегі желілік және фазалық кернеулер, токтар арасындағы қатынастар қандай түрде болады?

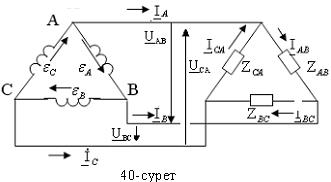
Дәріс. Қоректендіргіш пен қабылдағыштың фазаларының үшбұрыш сұлбасы бойынша жалғануы. Нөлдік сымсыз жұлдызша сұлбасы бойынша жалғанған үш фазалы тізбектегі симметриялы емес режим және оны есептеу

Қоректендіргіштің фазаларын үшбұрыш сұлбасы бойынша қосу үшін бір фазаның аяқы ұшын екінші фазаның басқы ұшымен, екінші фазаның аяқы ұшын үшінші фазаның басқы ұшымен, ал үшінші фазаның аяқы ұшын бір фазаның басқы ұшымен қосады (40-сурет). Сұлбада бейтарап сым болмайды. Сондықтан қоректендіргіштің желілік кернеулері оның фазалық кернеулеріне тең болады:

Егер U_AB = Е_А , U_BC = E_B , U_CA = E_C. Ом заңы бойынша қабылдағыштың фазалық токтары:

I_АВ= /Z_AВ =U_AВ/ Z_AВ, I_BС= E_B/Z_BС= U_BС/ Z_BС, I_CА= E_C/Z_CА= U_CА / Z_CA.

Егер қабылдағыш симметриялы (Z_AВ= Z_BС = Z_CА) болса, онда барлық фазалық токтардың әрекеттік мәндері бірдей болады және олардың желілік кернеулерге байланысты фазалық ығысулары да бірдей болады.

Кирхгофтың бірінші заңы бойынша желілік токтар: I_A= I_AB - I_CA, I_B= I_BC - I_AB, I_C= I_CA - I_BC. Бұл желілік және фазалық токтардың комплекстік мәндері үшін құрылған векторлық диаграмадағы токтар үшбұрышынан желілік токтардың модулдері мен фазалық токтардың модулдері арасында мынадай байланыс барынан көрінеді:

I_ж =2I_Фcos30˚= 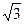I_Ф.

Үш фазалы тізбектің операторыдеп модулі 1-ге тең, фазасы 120⁰-қа тең комплекс санды атайды. Оны 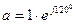, , 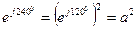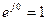;Үш вектор 1, а, а² симметриялы үш фазалы жүйе құрайды (41-сурет), сондықтан 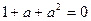; Кез-келген векторды операторға а көбейткенде ол вектордың модулі өзгермейді, бірақ ол 120⁰-қа бұрылады. Ал векторды а² көбейтсек, онда ол 240⁰ бұрылады. Операторды а пайдаланып E_B және E_C –ні E_A арқылы өрнектеуге болады: E_B=a² E_A, E_C= aE_A (42-сурет).

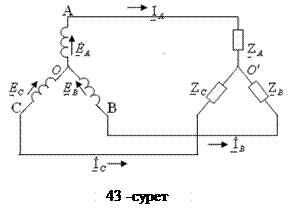Нөлдік сымсыз жұлдызша сұлбасы бойынша жалғанған симмериялы емес үш фазалы тізбек(43-сурет). Егер жүктеме симметриялы емес (Z_A ≠Z_B ≠Z_C) болса, сұлбаның екі түйіні ( О және О′ нүктелері) арасында потенциалдар айырымы - U_00′ кернеуі пайда болады. Бұл кернеуді анықтау үшін екі түйіндік потенциалдар тәсілін қолданамыз. Бұл тәсіл бойынша:

U_00′ = (Е_А Y_A + E_B Y_B + E_C Y_C)/( Y_A+ Y_B+ Y_C)= =(Е_А Y_A+ +a² E_A Y_B +a E_A Y_C)/( Y_A+ Y_B+ Y_C)= =Е_А (Y_A + a²Y_B +a Y_C)/( Y_A+ Y_B+ Y_C), мұндағы Y_A=1/Z_A, Y_B=1/Z_B, Y_C=1/Z_C – жүктеменің фазаларының комплекстік өткізгіштері.

Желілік токтарды анықтаймыз: I_A =U_A0′ / Z_A , I_B = U_B0′ / Z_B , I_C= U_C0′ / Z_C .

Бұл өрнектердегі кернеулер

U_A0′ = Е_А- U_00′ , U_B0′ = Е_B- U_{00′ ,} U_С0′ = Е_С- U_00′ .

Егер Z_A = Z_B = Z_C болса, онда Y_A = Y_B= Y_C=Y. Сондықтан U_00′ =Е_А Y (1 + a² +a )/3 Y =0.

Бұл жағдайда U_A0′ = Е_А, U_B0′ = Е_{B ′}, U_C0′ = Е_С , сол себепті де I_A = Е_А / Z_A , I_B = Е_B / Z_B , I_C= Е_С / Z_C;

Негізгі әдебиеттер: [1(156-168), 3(378-393)]

Қосымша әдебиеттер: [ 4,6,7,9,14 ]

Бақылау сұрақтары:

1.Қоректендіргіш пен қабылдағыштың фазаларының үшбұрыш сұлбасы бойынша жалғануына түсініктеме беріңіз. Токтар үшін векторлық диаграмма тұрғызыңыз.

2. Желілік токтарды фазалық токтар арқылы қалай табуға болады? Жүйе симметриялы болған кезде желілік токтардың модульдары мен фазалық токтардың модульдарының арасындағы қатынас қандай болады?

3. Үш фазалы тізбектің операторы дегенімз не? Оператор арқылы симметриялы э.қ.к.-тер қалай бейнелінеді?

4. Нөлдік сымсыз жұлдызша сұлбасы бойынша жалғанған симмериялы емес үш фазалы тізбек туралы түсініктеме беріңіз және есеп тәсіліне тоқталыңыз.

5. Осы тізбек симметриялы болса, онда есептеу жұмысы қалай жүргізіледі?

Дәріс. Үш фазалы тізбектердің қуаттары және оларды өлшеу. Өзара индуктивті байланысқан элементтері бар үш фазалы тізбектер. Үш фазалы желінің балама сұлбасы

Үш фазалы тізбектің активті қуаты жүктеменің фазаларының активті қуаттарының және нөлдік сымның кедергісінде бөлінетін активті қуаттың қосындысына тең:

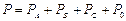,[Вт].

Үш фазалы тізбектің реактивті қуаты:

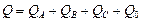, [ВАр].

Толық қуат: 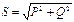, [ВА].

Жүктеме симметриялы болса болса, онда: , , , .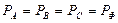

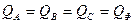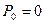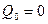Фазалық активті қуат: 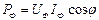; Фазалық реактивті қуат: 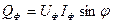. Үш фазалы тізбектің активті және реактивті қуаты: , .

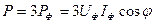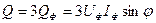Үш фазалы тізбектің толық қуаты: ;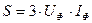

Жүктеменің фазаларының өзара жалғану сұлбаларына ( жұлдызша немесе үшбұрыш) байланыссыз үш фазалы тізбектің қуаттарын желілік кернеу мен желілік ток арқылы анықтауға болады.: , , ;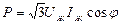

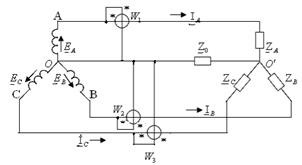
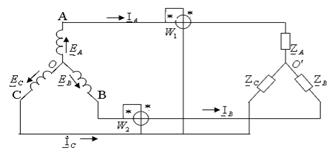
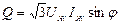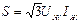Үш фазалы тізбектің активті қуатын өлшеу. Егер үш фазалы тізбекте нөлдік сым болса, бірақ жүктеменің фазаларының кедергілері Z_A , Z_B , Z_C бірдей болмаса, онда тізбектің активті қуатын өлшеу үшін үш ваттметр қолданылады (44-сурет).

44-сурет

45-сурет

Тізбектің активті қуаты осы үш ваттметр көрсетуінің қосындысына тең.

Егер тізбектің нөлдік сымы болмаса, онда активті қуатты өлшеу үшін екі ваттметр қолданылады (45-сурет). Бұл екі ваттметрдің көрсетуілері көбінесе бірдей болмайды. Бұл жағдайда үш фазалық жүйенің қуаты екі ваттметрдің көрсетулерінің алгебралық қосындысына тең.

Айталық, бірінші ваттметрдің көрсетуі P₁=Re[U_AC Ī_A] , ал екінші ваттметрдің көрсетуі P₂= Re[U_BC Ī_B]. Бұл жағдайда ваттметрлердің көрсетулерінің қосындысы

U_AC Ī_A+ U_BC Ī_B=( U_A - U_C) Ī_A+( U_B - U_C) Ī_B= U_A Ī+U_B Ī_B+ U_C Ī_C.

Соңғы өрнек үш фазаның активті қуаттарының қосындысын көрсетеді.

Егер жүктеме симметриялы болса, онда бір фазаның активті қуатын үшке көбейтеміз.

Өзара индуктивті байланысқан элементтері бар үш фазалы тізбектерді есептеубір фазалық синусоидалық токтың индуктивтік байланысы бар тізбегінің есебіне ұқсас жүргізіледі.

Үш фазалы желінің балама сұлбасынтұрғызу үшін желінің өнбойында болып жатқан электромагниттік құбылыстар есепке алынуы керек. Магниттік құбылыстарды индуктивтілк, электр өрісііне байланысты құбылыстарды сыйымдылық, ал жылу бөліну құбылысын кедергі арқылы сипаттайды.

Үш фазалы желінің балама сұлбасына оның сымдарының индуктивтілігі және сымдар арасындағы өзара индуктивтілік, сымдар мен жер арасындағы сиымдылық, сымдардың арасындағы сиымдылық, сымдарың активті кедергілері және оқшаулағыштардың ( изоляцияның) өткізгіштері енуі тиіс. 46 –суретте үш фазалы желінің бір фазасының «П » және «Т » тәрізді балама сұлбалары келтірілген. Суретте көрсетілген индуктивтілік L_ф симметриялы үш фазалы желінің индуктивтілігідеп