Дәріс. Активті кедергісі, идеал индуктивті элемент және сыйымдылық элементтер бірізді жалғанған тізбек
Бірізді жалғанған r, L және C элементтерден тұратын электр тізбегі арқылы ( 20-сурет) синусоидалы ток i=Imsin 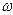 t жүргенде, осы тізбектегі кернеулердің лездік мәндері үшін Кирхгофтың екінші заңы бойынша теңдеу құруға болады: u= ur+uL+uC. Онда тізбек күйінің теңдеуі:
t жүргенде, осы тізбектегі кернеулердің лездік мәндері үшін Кирхгофтың екінші заңы бойынша теңдеу құруға болады: u= ur+uL+uC. Онда тізбек күйінің теңдеуі:
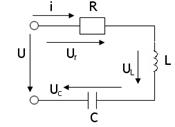 20-сурет 20-сурет
| u= ri+ L 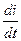 + + 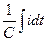 = rImsin = rImsin 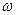 t+Im t+Im 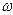 Lcos Lcos 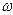 t - t - 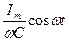 немесе
u=rImsin немесе
u=rImsin 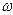 t+Im t+Im 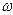 Lsin( Lsin( 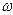 t+90o)+ t+90o)+ 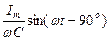 =Umrsin =Umrsin 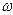 t+UmLsin( t+UmLsin( 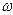 t++90o) +Umcsin( t++90o) +Umcsin( 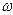 t - 90o).
Уақытқа тәуелді үш синусоидалы функцияның қосындысын комплекстік тәсілмен есептеген тиімді. Лездік кернеу мен ток негізінде комплекстік ток пен кернеуді жазайық: I t - 90o).
Уақытқа тәуелді үш синусоидалы функцияның қосындысын комплекстік тәсілмен есептеген тиімді. Лездік кернеу мен ток негізінде комплекстік ток пен кернеуді жазайық: I 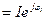 , ,
|
Ur 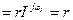 I, UL
I, UL 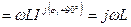 I , UC=
I , UC= 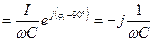 I , U=
I , U= 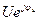 , j=ej90˚ , -j=e --j90˚
, j=ej90˚ , -j=e --j90˚
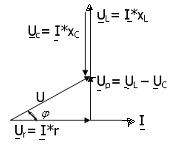
Комплекстік кернеулер мен токты векторлық диаграммада көрсетейік. Фаза бойынша Ur кернеу I токпен дәл келеді, UL фаза бойынша I токтан 90o алға озады, ал UC кернеуі фаза бойынша I токтан 90o
 21-сурет
21-сурет
 22-сурет 22-сурет
 23-сурет
23-сурет
| кеш қалады (17-сурет). Ur, UL, және UC векторларды қосу нәтижесінде U векторын аламыз. Бұл векторлар кернеулер үшбұрышын құрайды (21-сурет). Оның бір катетін активті кернеу Ur, екінші катеті реактивті кернеу Up= UL – UC , ал гипотенузаны толық кернеу U құрайды. Пифагор теоремасы бойынша: U= 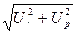 = = 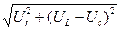 = = = = 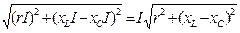 =Iz, мұндағы z =Iz, мұндағы z 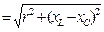 - толық кедергі. U кернеуінің векторымен I ток векторының арасындағы бұрыш - фазалық ығысуды φ анықтайды: φ= arctg - толық кедергі. U кернеуінің векторымен I ток векторының арасындағы бұрыш - фазалық ығысуды φ анықтайды: φ= arctg 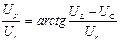 . Егер UL<UC болса, онда φ таңбасы теріс болады.
Кернеулер үшбұрышынан активті кернеуді Ua және реактивті кернеуді Up толық кернеу U мен фазалық ығысу φ арқылы табуға болады: Ua= Ur= Ucos φ ; Up= Usin φ.
Тізбектің толық кедергісінің z формуласындағы xL – xC айырмасын реактивті кедергі xp деп атайды, яғни xp= xL – xC..
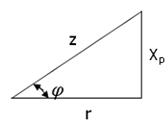
Толық кедергінің өрнегі бір катеті активті кедергіге r, екінші катеті реактивті кедергіге xp, ал гипотенузасы толық кедергіге z тең тікбұрышты үшбұрышқа сәйкес келеді. Бұл үшбұрышты кедергілер үшбұрышы деп атайды (22-сурет).
Бұл үшбұрыштан фазалық ығысу φ= arctg xp / r. Оның таңбасы xL < xC болғанда теріс болады.
Егер z және φ белгілі болса, онда кедергілер үшбұрышынан r = z cos φ ; xp= z sin φ. . Егер UL<UC болса, онда φ таңбасы теріс болады.
Кернеулер үшбұрышынан активті кернеуді Ua және реактивті кернеуді Up толық кернеу U мен фазалық ығысу φ арқылы табуға болады: Ua= Ur= Ucos φ ; Up= Usin φ.
Тізбектің толық кедергісінің z формуласындағы xL – xC айырмасын реактивті кедергі xp деп атайды, яғни xp= xL – xC..
Толық кедергінің өрнегі бір катеті активті кедергіге r, екінші катеті реактивті кедергіге xp, ал гипотенузасы толық кедергіге z тең тікбұрышты үшбұрышқа сәйкес келеді. Бұл үшбұрышты кедергілер үшбұрышы деп атайды (22-сурет).
Бұл үшбұрыштан фазалық ығысу φ= arctg xp / r. Оның таңбасы xL < xC болғанда теріс болады.
Егер z және φ белгілі болса, онда кедергілер үшбұрышынан r = z cos φ ; xp= z sin φ.
|
Лездік қуат: p= ui= 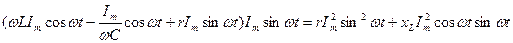 -
-
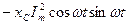 =
= 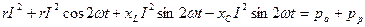 , мұндағы pa=
, мұндағы pa= 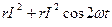 -активті лездік қуат; ал pp=
-активті лездік қуат; ал pp= 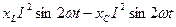 - реактивті лездік қуат;
- реактивті лездік қуат;
Активті лездік қуат pa=UaI – UaIcos2 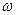 t= UIcos
t= UIcos 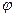 - UIcos
- UIcos 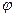 cos2
cos2 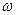 t, яғни ол тұрақты құраушыдан және айнымалы құраушыдан тұрады
t, яғни ол тұрақты құраушыдан және айнымалы құраушыдан тұрады 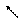 . Айнымалы құраушы екі еселенген жиілікпен өзгеретін, амлитудасы UIcos
. Айнымалы құраушы екі еселенген жиілікпен өзгеретін, амлитудасы UIcos 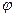 -ге тең косинусоида болады. Лездік қуаттың бір период ішіндегі орташа мәні активті қуат деп аталады. Ол лездік қуаттың тұрақты құраушысына тең: P= UI cos
-ге тең косинусоида болады. Лездік қуаттың бір период ішіндегі орташа мәні активті қуат деп аталады. Ол лездік қуаттың тұрақты құраушысына тең: P= UI cos 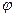 = uaI= rI2.
= uaI= rI2.
Индуктивті лездік қуат: pL= 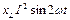 , сиымдылық лездік қуат: pC=
, сиымдылық лездік қуат: pC= 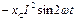 . Бұл қуаттардың фазалары қарама-қарсы. Тізбектің реактивті қуаты:
. Бұл қуаттардың фазалары қарама-қарсы. Тізбектің реактивті қуаты:
pp= pL+pC=( xL – xC) I2 sin2 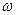 t = xp I2 sin2
t = xp I2 sin2 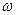 t = Up I sin2
t = Up I sin2 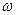 t= UI sinφsin2
t= UI sinφsin2 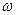 t.
t.
Лездік қуат: p= UIcos 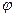 - UIcos
- UIcos 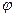 cos2
cos2 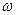 t + UIsin
t + UIsin 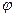 sin2
sin2 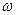 t = UIcos
t = UIcos 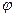 + UIsin(2
+ UIsin(2 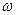 t+
t+ 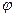 - 90o), яғни
- 90o), яғни
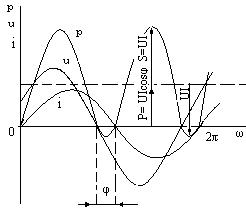 24-сурет
24-сурет
| ол тұрақты құраушыдан және айнымалы құраушыдан тұрады 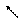 (24-сурет). Айнымалы құраушының амплитудасы UI тұрақты құраушыдан артық болғандықтан лездік қуат кейбір сәттерде теріс таңбалы болады. Бұл кезде тізбек қоректендіргішке энергияны қайтып береді. Қайтарылатын энергия тізбектің реактивті бөлігінің энергиясының есебінен жүреді. Айнымалы бөліктің амплитудасын S деп белгілейміз де, толық қуат деп атаймыз: S= IU. Өлшем бірлігі- вольтампер [ВА].
Лездік реактивті қуаттың амплитудасын (UIsin (24-сурет). Айнымалы құраушының амплитудасы UI тұрақты құраушыдан артық болғандықтан лездік қуат кейбір сәттерде теріс таңбалы болады. Бұл кезде тізбек қоректендіргішке энергияны қайтып береді. Қайтарылатын энергия тізбектің реактивті бөлігінің энергиясының есебінен жүреді. Айнымалы бөліктің амплитудасын S деп белгілейміз де, толық қуат деп атаймыз: S= IU. Өлшем бірлігі- вольтампер [ВА].
Лездік реактивті қуаттың амплитудасын (UIsin 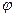 ) реактивті қуат Qp= UIsin ) реактивті қуат Qp= UIsin 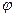 деп атайды. Өлшем бірлігі- вольтампер реактивтік [ВАр]. Qp= QL – QC= xLI2 – xCI2= ULI – UC I =Up I. деп атайды. Өлшем бірлігі- вольтампер реактивтік [ВАр]. Qp= QL – QC= xLI2 – xCI2= ULI – UC I =Up I.
|
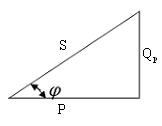
Кедергілер үшбұрышының қабырғаларын I2 көбейтсек, онда қуаттар үшбұрышын аламыз. Оның бір катеті активті қуатқа P, екінші катеті реактивті қуатқа Qp , ал гипотенузасы толық қуатқа S сәйкес келеді. Бұл үшбұрыштан толық қуат:S= 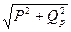 , φ= arctg Qp/ P, немесе P= Scos
, φ= arctg Qp/ P, немесе P= Scos 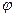 , Qp = Ssin
, Qp = Ssin 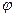 .
.
Әр түрлі электротехникалық қондырғыларда бір мезгілде электр энергиясының жылулық немесе механикалық энергияға айналуының қайтымсыз процестерімен қатар қайтымды процесс- электр энергиясының магнит энергиясына айналуы жүріп жатады. Активті қуат пайдалы жылуға немесе механикалық жұмысқа жұмсалатын болғандықтан электр энергиясының бір бөлігі ғана жұмсалады. Реактивті қуат пайдалы жұмыс жасамайды.
Активті қуаттың толық қуатқа қатынасын электротехникада қуат коэффициенті деп атайды: cos 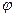 = P/ S.
= P/ S.
Негізгі әдебиеттер: [1(78-86, 94-98), 3( 152-156, 190-196)]
Қосымша әдебиеттер: [ 5,6,7,8]
Бақылау сұрақтары:
1. Бірізді жалғанған r, L және C элементтерден тұратын электр тізбек күйінің теңдеуіне түсініктеме беріңіз.
2.Векторлық диаграммада токтың және кернеулердің векторларының өзара орналасуы. Кернеулер үшбұрышы. Активті, реактивті және толық кернеулер.
3. Кедергілер үшбұрышы. Тізбектің активті, реактивті және толық кедергілері.
4. Тізбектің лездік қуаты. Активті, реактивті және толық қуат.
5. Қуаттар үшбұрышы. Қуат коэффициенті.
Дата добавления: 2015-09-11; просмотров: 5132;
