Лабораторна робота 123. ДОСЛІДЖЕННЯ ПРЕЦЕСІЇ ГІРОСКОПА ТА ВИЗНАЧЕННЯ ЙОГО МОМЕНТУ ІНЕРЦІЇ
Завдання:визначити момент інерції гіроскопа.
Приладдя: дослідна установка.
Теоретичний матеріал: момент сили, момент інерції твердого тіла, рівняння моментів, закон збереження моменту імпульсу, рух вільного гіроскопа, вимушена прецесія гіроскопа, тензор інерції.
Література:
1. Р.4. §§. 4.1 - 4.6;
2. Р.4. §.§. 4.2, 4.8 ;
3. §§. 9.1 – 9.5;
4. §. 36 - 41;
5. §. 21, 24, 31, 32, 35.
 Опис установки.На основі з чотирма ніжками, висоту яких можна змінювати (вирівнювати установку), закріплені блок керування 1 та колонка 2 (рис.1). До колонки прикріплений кронштейн, на якому у вилці 3 змонтовано гіроскоп з електро-приводом 4 та фотоелектричний датчик для вимірювання кута повороту гіроскопа у горизонталь-ній площині. Гіроскоп з електро-приводом та вилкою може обертатися навколо вертикальної осі, а гіроскоп з
Опис установки.На основі з чотирма ніжками, висоту яких можна змінювати (вирівнювати установку), закріплені блок керування 1 та колонка 2 (рис.1). До колонки прикріплений кронштейн, на якому у вилці 3 змонтовано гіроскоп з електро-приводом 4 та фотоелектричний датчик для вимірювання кута повороту гіроскопа у горизонталь-ній площині. Гіроскоп з електро-приводом та вилкою може обертатися навколо вертикальної осі, а гіроскоп з
|
На основі установки розміщений також блок живлення електропривода гіроскопа та вимірювання параметрів його руху. На передній панелі блока є кнопки „сеть”, „сброс”, „стоп”; ручка потенціометра, за допомогою якої вмикають напругу живлення електропривода гіроскопа та змінюють швидкість його обертання; покажчик швидкості обертання гіроскопа, цифровий індикатор кута повороту гіроскопа та мілісекундомір.
Виведення робочої формули. Гіроскопом називається тверде тіло з великим моментом інерції відносно осі симетрії. Теорія руху гіроскопа ґрунтується на рівнянні моментів
 , (1)
, (1)
де 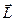 – момент імпульсу,
– момент імпульсу, 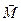 – момент сили. Це рівняння аналогічне до другого закону Ньютона для поступального руху:
– момент сили. Це рівняння аналогічне до другого закону Ньютона для поступального руху:
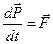 , (2)
, (2)
де  – імпульс тіла,
– імпульс тіла, 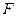 – сила.
– сила.
Якщо точка опори гіроскопа збігається з його центром мас, то на гіроскоп не діють зовнішні моменти сил тяжіння; якщо ж нема яких-небудь зовнішніх сил, то гіроскоп називається вільним. У цьому випадку  і момент імпульсу
і момент імпульсу  (
(  і тоді, якщо сума зовнішніх моментів сил дорівнює нулю).
і тоді, якщо сума зовнішніх моментів сил дорівнює нулю).
З теорії руху гіроскопа випливає таке: якщо він обертається навколо осі симетрії, то його момент імпульсу можна виразити через добуток моменту інерції гіроскопа 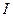 та його кутової швидкості обертання
та його кутової швидкості обертання  :
: 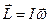 , аналогічно до
, аналогічно до 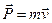 для поступального руху. Отже, якщо
для поступального руху. Отже, якщо  , то постійними є напрям осі обертання (бо, як відомо, вектор
, то постійними є напрям осі обертання (бо, як відомо, вектор  збігається з віссю обертання) та значення вектора
збігається з віссю обертання) та значення вектора  , тобто кутова швидкість обертання. Якщо обертання виконується навколо будь-якої іншої осі, то
, тобто кутова швидкість обертання. Якщо обертання виконується навколо будь-якої іншої осі, то  , як в попередньому випадку, однак напрям осей обертання і симетрії відрізняється від напряму
, як в попередньому випадку, однак напрям осей обертання і симетрії відрізняється від напряму 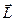 (
( 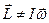 ). Можна довести, що тоді вісь симетрії (її називають віссю фігури) рівномірно обертається навколо вектора
). Можна довести, що тоді вісь симетрії (її називають віссю фігури) рівномірно обертається навколо вектора 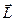 , описуючи поверхню конуса. Рух цього типу називають вільною прецесією гіроскопа.
, описуючи поверхню конуса. Рух цього типу називають вільною прецесією гіроскопа.
Якщо  , тобто якщо на гіроскоп діють зовнішні моменти сил, сума яких не дорівнює нулю, але гіроскоп обертається точно навколо осі симетрії, то він виконує новий тип руху, який називають вимушеною прецесією.
, тобто якщо на гіроскоп діють зовнішні моменти сил, сума яких не дорівнює нулю, але гіроскоп обертається точно навколо осі симетрії, то він виконує новий тип руху, який називають вимушеною прецесією.
Виведемо формулу, яка виражає закон вимушеної прецесії. Нехай на вісь гіроскопа, який обертається зі сталою кутовою швидкістю  навколо осі симетрії, почала діяти деяка зовнішня сила
навколо осі симетрії, почала діяти деяка зовнішня сила  , момент інерції якої відносно осі обертання дорівнює
, момент інерції якої відносно осі обертання дорівнює 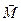 . Припустимо, що під дією цього зовнішнього моменту вісь гіроскопа повернулася на нескінченно малий кут
. Припустимо, що під дією цього зовнішнього моменту вісь гіроскопа повернулася на нескінченно малий кут  і внаслідок цього момент імпульсу змінився на
і внаслідок цього момент імпульсу змінився на  (зміна настала внаслідок зміни напряму вектора
(зміна настала внаслідок зміни напряму вектора 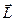 без зміни його модуля
без зміни його модуля  (рис. 2).
(рис. 2).
Згідно з рівнянням моментів 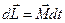 , тобто напрям
, тобто напрям  збігається з напрямом моменту сили
збігається з напрямом моменту сили 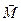 . Отже, поворот навколо осі
. Отже, поворот навколо осі  , перпендикулярної до площини рисунка, відбувається під дією моменту сили, напрям вектора якого паралельний до напряму вектора
, перпендикулярної до площини рисунка, відбувається під дією моменту сили, напрям вектора якого паралельний до напряму вектора  . Отже, під час дії на гіроскоп моменту сили
. Отже, під час дії на гіроскоп моменту сили 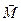 вектор кутової швидкості обертання гіроскопа
вектор кутової швидкості обертання гіроскопа  повертається у напрямі до збігання з напрямом вектора
повертається у напрямі до збігання з напрямом вектора 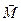 , виконуючи таким чином прецесійний рух. Кутову швидкість прецесії
, виконуючи таким чином прецесійний рух. Кутову швидкість прецесії  можна визначити з формули, яка зв’язує
можна визначити з формули, яка зв’язує  і
і  :
:
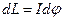 .
.
Продиференціюємо цей вираз по часу: 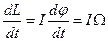 , звідки з урахуванням (1) одержимо:
, звідки з урахуванням (1) одержимо:
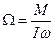 . (3)
. (3)
Напрями векторів 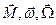 пов’язані співвідношенням
пов’язані співвідношенням
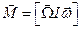 .
.
Останнє співвідношення можна отримати з формули Пуансо, яка стверджує:
 Якщо якийсь вектор
Якщо якийсь вектор 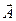 (у нашому випадку його роль відіграє вектор
(у нашому випадку його роль відіграє вектор 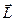 ) оберта-ється з кутовою швидкістю
) оберта-ється з кутовою швидкістю  , не змінюючи свого значення, то
, не змінюючи свого значення, то 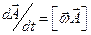 .
.
Якщо  перпенди-кулярний до
перпенди-кулярний до 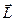 , то
, то
 , або
, або
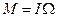 (5)
(5)
Ця формула виражає закон вимушеної прецесії гіроскопа.
У нашому випадку
|
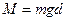 , (6)
, (6)
де  – маса тягарця 3 (див. рис. 1);
– маса тягарця 3 (див. рис. 1); 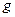 - прискорення вільного падіння;
- прискорення вільного падіння;  – плече сили
– плече сили  , яка діє на вісь гіроскопа.
, яка діє на вісь гіроскопа.
Кутову швидкість прецесії  можна одержати, вимірявши час
можна одержати, вимірявши час  , впродвж якого гіроскоп повернувся на кут
, впродвж якого гіроскоп повернувся на кут 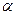 радіанів унаслідок прецесійного руху. Тоді
радіанів унаслідок прецесійного руху. Тоді
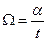 . (7)
. (7)
Підставивши формули (6) і (7) у вираз (5) та врахувавши, що 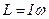 , одержимо робочу формулу для визначення моменту інерції гіроскопа
, одержимо робочу формулу для визначення моменту інерції гіроскопа
 . (8)
. (8)
Перевівши радіани у градуси, а кутову швидкість – у частоту обертання гіроскопа, одержимо робочу формулу в величинах, які безпосередньо вимірюємо:
 . (9)
. (9)
Дата добавления: 2015-09-11; просмотров: 1099;
