Лабораторна робота 122. ВИВЧЕННЯ КОЛИВНИХ ПРОЦЕСІВ

Завдання: дослідити вільні, згасаючі і вимушені коливання, визначити циклічну частоту вільних коливань, логарифмічний декремент згасання згасаючих коливань і дослідити явище резонансу.

Приладдя: лабораторна установка.

Теоретичний матеріал, який потрібно засвоїти під час підготовки до виконання роботи: пружна (квазіпружна) сила; гармонічні коливання їхнє рівняння та розв’язок; амплітуда, частота, фаза; згасаючі коливання, їхнє рівняння та розв’язок; коефіцієнт згасання, логарифмічний декремент згасання; вимушені коливання, їхнє рівняння та розв’язок; явище резонансу.

Література:

1. § 63-67, с.166-178.

2. § 9.1-9.6, с.119-129; § 9.12-9.13, с.137-148.

3. § 15.1-15.9, с.144-171.

4. § 10.1-10.5, с.209-222; § 10.8-10.9, с.231-240.

Опис установки.Установка змонтована на основі, що має чотири ніжки, висоту яких можна змінювати (вирівнювати установ-ку). На основі прикріплені колонка 1 та електронний блок 2, який складається з мілісекундоміра, лічильника періодів, електропри-воду шатуна і кнопок керування. На колонці закріплені два кронштейни. До верхнього кронштейна кріпляться підвіски 3, на яких на підшипниках підвішений маятник 4 i шатун 5. На стеблі маятника закріплені переривач світлового потоку 6 та гальмівний прапорець 7, який слугує для зміни коефіцієнта лобового опору маятника. Вимушені коливання рис.10. збуджують за допомогою диска, закріпленого на валу електродвигуна, який коливає шатун, з’єднаний пружинами 8 зі стеблом маятника. До шатуна прикріплений рухомий переривач світлового потоку, призначений для визначення частоти коливань шатуна (частоти вимушувальної сили).

До нижнього кронштейна прикріплена кутова, шкала 9, за допомогою якої визначають амплітуду коливань маятника. В кронштейні вмонтований фотоелектричний датчик, який у разі проходження крізь нього прапорця і переривання світлового потоку вмикає мілісекундомір та лічильник кількості коливань.

Ідея роботи та виведення робочих формул. У цій роботі досліджують вільні, згасаючі й вимушені коливання. Розглянемо ці коливання на прикладі матеріальної точки. Вільні коливання матеріальна точка виконує лише тоді, коли на неї діє сила F, величина якої прямо пропорційна зміщенню x точки від положення рівноваги. Таку силу називають квазіпружною (F=-kx). За умови, коли, крім квазіпружної, на точку діє ще й сила опору (F_o= - rv), коливання будуть згасаючими. Коливальна система під час таких коливань поступово втрачатиме свою енергію, і амплітуда коливань зменшуватиметься з часом. Якщо ж на матеріальну точку, поряд із двома згаданими вище силами, діє ще й зовнішня періодична сила F₃= F₀cos w_вt, тоді коливання будуть вимушеними.

Закони динаміки, які описують ці три види коливань, запишемо так:

ma= -kx– для вільних; (1)

ma= -kx –rv– для згасаючих; (2)

ma= -kx –rv + F₀cos w_вt– для вимушених, (3)

де x – зміщення; v – швидкість; a – прискорення точки, що коливається; r - коефіцієнт опору; F₀ і w_в – амплітуда і циклічна частота зовнішньої (збуджувальної) сили.

Врахуємо тепер, що a=d²x/dt², a v=dx/dt. Це дає змогу легко звести рівняння (1) – (3) до вигляду диференціальних рівнянь другого порядку.

Для вільних коливань – , (4)

де – циклічна частота вільних (власних) коливань;

для згасаючих – , (5)

де 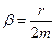– коефіцієнт згасання;

для вимушених – 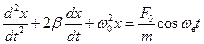. (6)

Розв'язками цих рівнянь є, відповідно, функції

x = A₀ cos(w₀t+j),(7)

де A₀ i w₀ – амплітуда і частота вільних коливань; j – початкова фаза;

x = A cos(wt+j) =A₀ exp(-b/t) cos(wt+j), (8)

де A= A₀ exp(-b/t) – амплітуда, a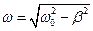– частота згасаючих коливань;

x = A_в cos(w_вt - j), (9)

деА_в і w_в– амплітуда та частота вимушених коливань,

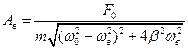.(10)

Як бачимо, амплітуда згасаючих коливань зменшується з часом за законом експоненти, а амплітуда вимушених залежить від співвідношення частот w_в і w₀.

За означенням частота коливань n = 1/T, або n = n/t, де T – період коливань, n – кількість коливань, t – час, за який коливна система виконує n коливань. Циклічна частота

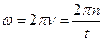. (11)

У випадку згасаючих коливань відношення двох послідовних амплітуд А_n/A_n+1 має стале значення, його називають декрементом згасання q, а логарифм цього відношення lnq – логарифмічним декрементом згасання d. З урахуванням (8) отримаємо

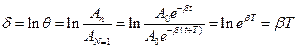. (12)

В умовах експерименту, коли загасання коливань незначне, користуватись формулою (12) для визначення логарифмічного декремента загасання d незручно, оскільки різниця послідовних амплітуд невелика. З огляду на це ліпше вимірювати амплітуди коливань А₁ і А₂ через достатньо великий проміжок часу Dt = t₂-t₁. Нехай у момент часу t₁ амплітуда згасаючих коливань становить

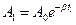, (13)

а в момент часу t₂

. (14)

Розділивши почленно ці вирази, отримаємо

, (15)

або після логарифмування

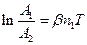. (16)

Звідси , (17)

а логарифмічний декремент згасання

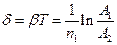, (18)

де n₁ – кількість коливань за час , впродовж якого амплітуда зменшується від А₁ до А₂; Т – період коливань.

Із формул (17) і (18) легко зрозуміти фізичний зміст коефіцієнта згасання та логарифмічного декременту згасання:

коефіцієнт згасання b є фізичною величиною, оберненою до проміжку часу 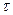, впродовж якого амплітуда коливань зменшується, в e разів;

логарифмічний декремент згасання d є фізичною величиною, оберненою до кількості коливань n_e, впродовж яких амплітуда коливань зменшується в е разів.

Тепер проаналізуємо рівняння, які описують вимушені коливання. Із (9) і (10) легко бачити, що частота вимушених коливань відповідає частоті w_в, а амплітуда коливань А_в залежить від співвідношення між частотою власних коливань системи w₀ і частотою зовнішньої збуджувальної сили w_в. За наближення частоти зовнішньої сили до частоти власних коливань системи амплітуда коливань різко збільшується. Таке явище називають резонансом, а частоту, за якої амплітуда коливань досягає максимального значення, – резонансною. Зі співвідношення (10) і наведених вище міркувань легко довести, що

. (19)

Отже, резонансна частота завжди менша від частоти власних коливань, якщо в системі діють сили опору. Експериментально w_резвизначають як частоту зовнішньої сили (у цій роботі це частота коливань шатуна), за якої простежується максимум амплітуди коливань.