Лабораторна робота 121. ПЕРЕВІРКА ТЕОРЕМИ ГЮЙГЕНСА-ШТЕЙНЕРА ЗА ДОПОМОГОЮ ТРИФІЛЯРНОГО ПІДВІСУ

Завдання: перевірити теорему Гюйгенса-Штейнера.

Приладдя: трифілярний підвіс, два циліндри, вага, секундомір.

Теоретичний матеріал: момент сили, момент інерції матеріальної точки та твердого тіла, центр мас, теорема Гюйгенса-Штейнера, основний закон динаміки обертального руху, кінетична енергія обертального руху, закон збереження механічної енергії, гармонічні коливання та їхні характеристики, крутильні коливання трифілярного підвісу та їхній період.

Література:

1. Р.4. §§. 4.1 - 4.3; Р.10. §.10.5;

2. Р.4. §.§. 4.2, 4.4 – 4.6; Р.8. §. 8.5;

3. §§. 9.1 – 9.8;

4. §. 36 - 40; §. 64;

5. §. 32 §.34.

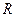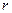Опис установки. Момент інерції тіла довільної форми можна виміряти за допомогою трифілярного підвісу (рис.1). Трифілярний підвіс – це кругла плоска платформа 1 у вигляді диска радіусом , підвішена на трьох симетрично розміщених по вершинах рівнобічного трикутника нитках 2 довжиною . Верхні кінці ниток закріплені до невеликого диска 3 радіусом , який кріплять до спеціального кронштейна, вмонтованого в стіну. Під час повороту верхнього диска на невеликий кут 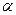навколо вертикальної осі, перпендикулярної до площини диска, усі три нитки набувають нахиленого положення, центр мас платформи трохи піднімається по осі обертання і вона починає виконувати крутильні коливання, період яких залежить від моменту інерції платформи. Платформі надають коливального руху поворотом верхнього диска за допомогою шнура, який приводить у рух важіль, зв’язаний з верхнім диском. У разі цього платформа виконує крутильні коливання навколо вертикальної осі без коливань, подібних до плоских коливань маятника, які утруднюють вимірювання.

Виведення робочих формул. Платформа масою 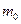, повертаючись на трифілярному підвісі, вертикально коливається. Вона піднімається за чверть періоду на висоту . Потенціальна енергія, що її одержала платформа протягом наступної чверті періоду, переходить у кінетичну енергію обертального руху і це повторюватиметься через кожну чверть періоду крутильних коливань. Нехтуючи тертям, запишемо закон збереження механічної енергії:

, (1)

де –прискорення вільного падіння. – момент інерції платформи, – максимальна кутова швидкість платформи (під час її проходження через положення рівноваги).

Кутову швидкість платформи можна визначити, продиференціювавши рівняння, яке описує кутове зміщення платформи під час її крутильних коливань:

. (2)

Тоді , звідки

. (3)

Повертання платформи на кут навколо осі ОО₁ відповідає її підніманню на висоту (рис.2):

.

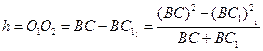Позначимо через довжину ниток , а через 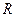і 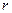відповідно відстань від точок їхнього кріплення на платформі та диску до осі обертання ОО . З трикутника АВС і А ВС одержимо таке співвідношення :

Отже, висота підняття платформи :

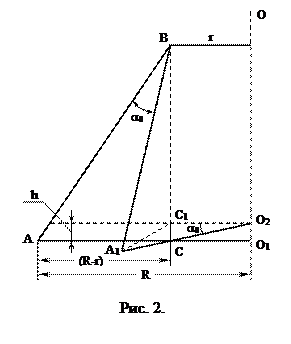Якщо довжина ниток значна і кути відхилення платформи малі , то можна вважати, що

і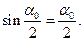

Тоді, щоб визначити , одержуємо формулу

(4)

З формул (1),(3) і (4) визначаємо вираз для обчислення моменту інерції не навантаженої платформи трифілярного підвісу

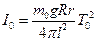(5)

Платформа, навантажена досліджуваним тілом масою 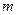, буде коливатися з періодом 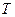, а момент інерції системи “платформа + досліджуване тіло ” можна визначити за формулою

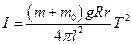. (6)

Очевидно , різниця моментів інерції, які обчислюють за формулами (6) та (5), і буде моментом інерції досліджуваного тіла.

Виконуючи завдання, треба користуватися низкою інших робочих формул, иведення яких наводимо з міркувань зручності нижче.