Форма звіту до лабораторної роботи 119.

1. Завдання.

2. Рисунок установки.

3. Робоча формула з розшифруванням величин.

4. Формула для обчислення похибок:

.

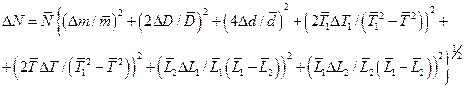
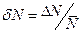5. Результати вимірювань та обчислень:

; ; ; ;

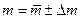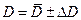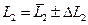
Номер за пор.	ti, c	Dti, c	Ti, c	DTi, c	t1i, c	Dt1i, c	T1i, c	DT1i, c	N, н/м2	DN, н/м2	N, %
1 – 5
с/зн.

; ; ; .

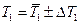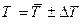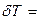6. Кінцевий результат:

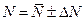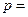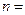; = . ; 5.

7. Висновки.

Лабораторна робота 120. ВИЗНАЧЕННЯ МОДУЛЯ ЗСУВУ ДИНАМІЧНИМ МЕТОДОМ

Завдання: визначити модуль зсуву матеріалу дротини шляхом дослідження коливань крутильного маятника.

Приладдя:крутильний маятник, технічні терези, секундомір, лінійка, мікрометр.

Теоретичний матеріал, який потрібно засвоїти під час підготовки до виконання роботи: деформація твердих тіл; деформація кручення та зсуву; закон Гука; модуль зсуву; модуль кручення; момент сили; момент інерції; крутильні коливання.

Література:

1. Р.5. §§. 5.2 - 5.4;

2. Р.2. §§. 2.12 – 2.14; Р.5 §.5.9.3.

3. §.§. 7.11; 11;

4. §. 19.

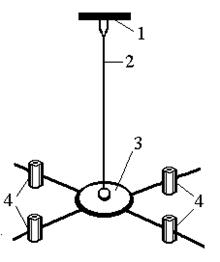Опис установки. Установка для визначення модуля зсуву динамічним методом складається з підставки, до верхнього кронштейна 1 якої нерухомо підвішений тонкий стрижень 2 із досліджуваного матеріалу. До нижнього кінця стрижня прикріплена хрестовина 3, на яку можна встановлювати i закріплювати на різних відстанях від осі стрижня додаткові вантажі 4.

Ідея роботи та виведення робочої формули.Якщо до стрижня прикласти пару сил із моментом сили М, спрямованим вздовж осі стрижня, то він здеформується так, що його нижня основа повернеться відносно верхньої на кут φ. Деформація кручення аналогічна до деформації зсуву. Якщо умовно розбити стрижень на елементарні шари, перпендикулярні до його осі, то закручування призведе до зсуву кожного шару щодо сусідніх. Зсув буде неоднорідним, оскільки він залежить від відстані до осі. Можна довести, що залежність кута закручування від довжини стрижня L, його радіуса R, пружних властивостей i обертального моменту сили М описує співвідношення

, (1)

де 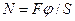– модуль зсуву, який чисельно дорівнює значенню дотичного механічного напруження за одиничного відносного зсуву. Якщо у формулі (1) позначити сталий множник при М через c, то отримаємо закон Гука для деформації кручення:

. (2)

Величину, обернену до c , називають модулем кручення b,

. (3)

На підставі співвідношень (1) - (3) можна довести, що між модулем кручення b i модулем зсуву N існує залежність

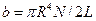. (4)

Отже, модуль зсуву матеріалу стрижня легко отримати, визначивши його модуль кручення. Відповідно, модуль кручення можна визначити, досліджуючи коливання кру-тильного маятника, оскільки період його коливань залежатиме від модуля кручення стрижня підвісу. Розглянемо коливання такого маятника детальніше. Якщо хрестовинa маятника здійснює крутильні коливання, то їх можна описати основним законом обертального руху:

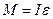, (5)

де М – обертальний момент; І – момент інерції маятника; – його кутове прискорення. Використавши формулу (3), основний закон обертального руху можна записати у вигляді

(6)

Із цього рівняння випливає, що кутове прискорення маятника пропорційне до кутового зміщення φ і спрямоване в протилежний бік від нього. Розв’язком цього рівняння є гармонічна функція

j = j₀ cos wt. (7)

Тут w - це циклічна частота коливань,

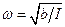. (8)

З іншого боку, оскільки 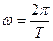, ми отримуємо формулу для періоду крутильних коливань маятника

. (9)

Як бачимо, з формули (9) можна отримати модуль кручення, якщо відомі момент інерції коливальної системи І та період її коливань Т. У випадку крутильних коливань маятника його період визначають експериментально, а момент інерції невідомий. Для того, щоб вилучити з формули (9) невідомий момент інерції системи I, врахуємо, що

І=І₀+4mr², (10)

де І₀ – сталий момент інерції хрестовини і стрижня маятника, а 4mr² – момент інерції чотирьох додаткових вантажів, що розміщені на ній на відстані r від осі обертання. Отже, змінюючи положення додаткових вантажів, отримаємо значення двох різних моментів інерції системи І₁ i І₂, яким відповідають періоди коливань Т₁ i Т₂ . Ці моменти інерції запишемо згідно з (10) як

і 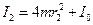. (11)

З іншого боку, ці ж моменти інерції можна визначити зі співвідношення (9), зокрем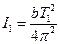а

, а 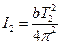. (12)

Знайдемо тепер різницю цих моментів інерції

і (13)

. (14)

Прирівнявши праві частини рівнянь (13) і (14), одержимо 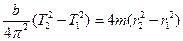, звідки

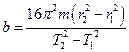. (15)

Врахувавши зв’язок між модулем кручення b i модулем зсуву N (4), отримаємо робочу формулу, яка містить середні значення величин, виміряних експериментально.

. (16)