Формула Бейеса (теорема гипотез)
Если до опыта вероятности гипотез 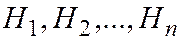 были равны соответственно
были равны соответственно 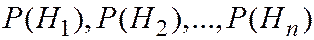 , а в результате опыта произошло событие
, а в результате опыта произошло событие 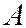 , то новые (условные) вероятности гипотез вычисляются по формуле
, то новые (условные) вероятности гипотез вычисляются по формуле
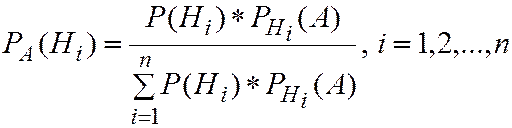 (2.21)
(2.21)
Вероятности 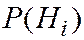 называются априорными (до опытными),
называются априорными (до опытными),
Вероятности 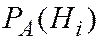 - апостериорными (после опытными).
- апостериорными (после опытными).
Формула Бейеса (2.21) дает возможность «пересмотреть» возможности (переоценить вероятности) гипотез с учетом результата испытания.
Пример. По каналу связи, на который могут действовать помехи, передается одна из двух кодовых комбинаций 111 или 000 с вероятностями 0,8 и 0,2 соответственно. Через помехи вероятность верного получения каждого из символов комбинации равна 0,6. Считается, что символы кодовых комбинаций искажаются независимо друг от друга. Определить, какая кодовая комбинация была отправлена, если получена – 000.
Решение.
Гипотезы 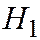 - отправлена комбинация 111
- отправлена комбинация 111
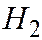 - 000
- 000
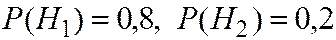
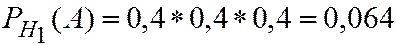
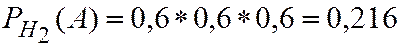
По (2.20) 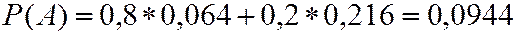
По (2.21)
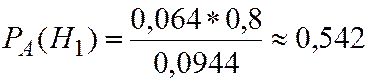
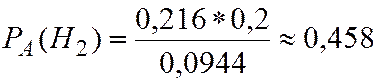
Сравнив 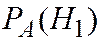 и
и 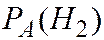 , делаем вывод, что при полученной комбинации 000 вероятнее была отправлена комбинация 111.
, делаем вывод, что при полученной комбинации 000 вероятнее была отправлена комбинация 111.
Формула Бернулли
Если производится 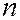 независимых опытов, в каждом из которых событие A появляется с вероятностью
независимых опытов, в каждом из которых событие A появляется с вероятностью 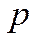 , то вероятность того, что событие A произойдет в этих
, то вероятность того, что событие A произойдет в этих 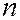 опытах ровно
опытах ровно 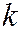 раз, выражается формулой Бернулли
раз, выражается формулой Бернулли
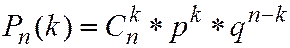 ,
, 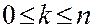 (2.22)
(2.22)
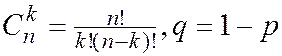
Формула (2.22) выражает так называемое биномиальное распределение вероятностей и применяется, как правило, если 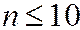
Пример. Сообщение передается серией кодированных сигналов. В серии из десяти сигналов, вероятность получения каждого сигнала 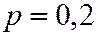 . Сообщение считается принятым, если из серии получено четыре сигнала. Какова вероятность принять переданное сообщение.
. Сообщение считается принятым, если из серии получено четыре сигнала. Какова вероятность принять переданное сообщение.
Решение.
Событие 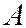 - сигнал принят,
- сигнал принят, 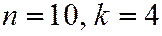
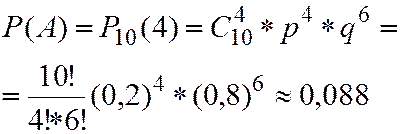
Значение 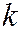 , при котором
, при котором 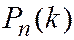 превышает или, по крайней мере, не меньше, вероятности остальных возможных исходов испытания называют наивероятнейшим,обозначают
превышает или, по крайней мере, не меньше, вероятности остальных возможных исходов испытания называют наивероятнейшим,обозначают 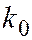 и определяют из двойного неравенства
и определяют из двойного неравенства
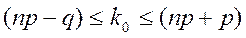 (2.23)
(2.23)
При этом, если
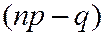 - дробное, то существует одно наивероятнейшее число
- дробное, то существует одно наивероятнейшее число 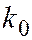 ;
;
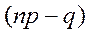 - целое, то существует два наивероятнейших числа:
- целое, то существует два наивероятнейших числа: 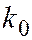 и
и 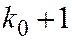 ;
;
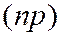 - целое, то
- целое, то 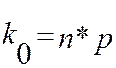 .
.
Пример.Вероятность того, что в течении одного дня на предприятии будет перерасход воды равна 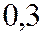 . Определить наиболее вероятное число дней в течении месяца (30-ти дней) с нормальным расходом воды.
. Определить наиболее вероятное число дней в течении месяца (30-ти дней) с нормальным расходом воды.
Решение.
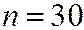 ,
, 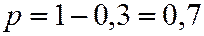
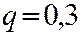
По (2.23)
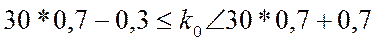
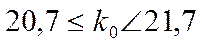
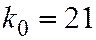
Формула Пуассона
Если число 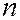 независимых испытаний достаточно велико
независимых испытаний достаточно велико 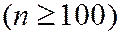 , а вероятность
, а вероятность 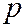 появления события
появления события 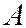 в каждом испытании постоянна и мала
в каждом испытании постоянна и мала 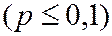 , и
, и 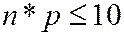 , то вместо (2.22) используют асимптотическую формулу Пуассона
, то вместо (2.22) используют асимптотическую формулу Пуассона
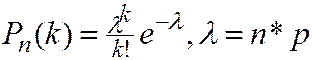 (2.24)
(2.24)
Пример. Радиоприбор состоит из 1000 элементов, которые работают независимо друг от друга. Каждый из них может выйти из строя с вероятностью 0,002. Вычислить вероятность того, что во время работы прибора из строя выйдут от 3 до 6 элементов.
Решение.
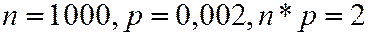
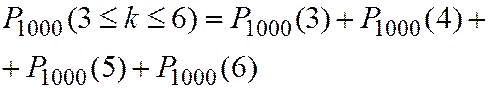
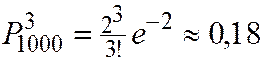
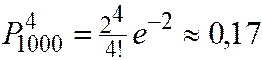
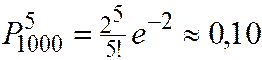
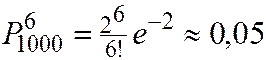
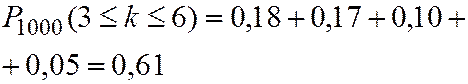
Дата добавления: 2015-11-18; просмотров: 670;
