Формы закона распределения дискретной случайной величины
Ряд распределения дискретной случайной величины 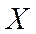 -это таблица, в которой перечислены в порядке возрастания все возможные различные значения этой случайной величины
-это таблица, в которой перечислены в порядке возрастания все возможные различные значения этой случайной величины 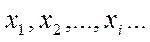 с соответствующими им вероятностями
с соответствующими им вероятностями 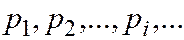
| 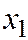
| 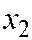
| 
| 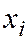
| 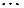
|
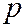
| 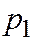
| 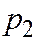
| 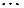
| 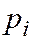
| 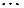
|
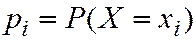
Т.к. в результате испытания 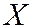 принимает только одно из приведенных значений, то события
принимает только одно из приведенных значений, то события 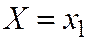 ,
,  , …,
, …, 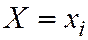 , … образуют полную группу и
, … образуют полную группу и
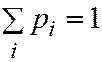 (3.1)
(3.1)
Формула (3.1) называется условием нормировки ДСВ.
Многоугольник распределения ДСВ –графическое изображение ряда распределения ДСВ в декартовой системе координат.

Многоугольник распределения для ДСВ 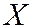 , принимающей значения
, принимающей значения 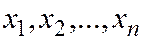 с вероятностями
с вероятностями 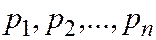 соответственно.
соответственно.
Аналитическая формапредставление закона распределения ДСВ с помощью формулы
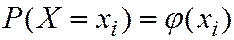
Функция распределения 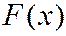 ДСВ
ДСВ 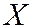 есть разрывная, ступенчатая функция, скачки которой соответствуют возможным значениям
есть разрывная, ступенчатая функция, скачки которой соответствуют возможным значениям 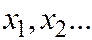 случайной величины
случайной величины 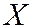 и равны вероятностям
и равны вероятностям 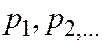 этих значений. Между скачками функция
этих значений. Между скачками функция 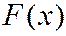 сохраняет постоянное значение. В точке разрыва функция
сохраняет постоянное значение. В точке разрыва функция 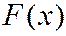 равна тому значению, с которым она подходит к точке разрыва слева, т.е.
равна тому значению, с которым она подходит к точке разрыва слева, т.е. 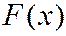 - непрерывна слева.
- непрерывна слева.

График функции распределения ДСВ 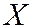 , принимающей значения
, принимающей значения 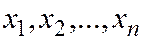 .
.
Плотность распределения не используется для представления закона распределения ДСВ.
Пример. Устройство состоит из 3-х независимо работающих элементов. Вероятность того, что элемент не сработает в данном испытании 0,1. Привести все формы представления закона распределения случайной величины 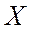 равной числу несработавших элементов.
равной числу несработавших элементов.
Решение.
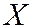 - ДСВ. Возможные значения
- ДСВ. Возможные значения
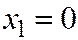 - все элементы работающие;
- все элементы работающие;
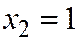 - не сработал 1 элемент;
- не сработал 1 элемент;
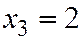 - не сработало 2 элемента;
- не сработало 2 элемента;
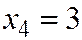 - не сработали 3 элемента.
- не сработали 3 элемента.
Вероятность каждого из возможных значений ДСВ 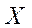 можно рассчитать по формуле Бернулли (2.22), которая для данного примера будет являться аналитической формой закона распределения.
можно рассчитать по формуле Бернулли (2.22), которая для данного примера будет являться аналитической формой закона распределения.
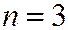 ,
, 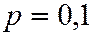 ,
, 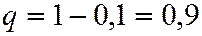
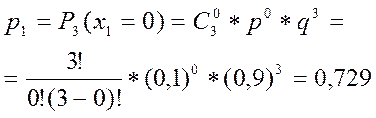
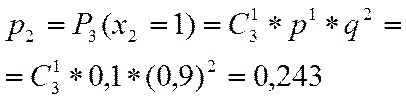
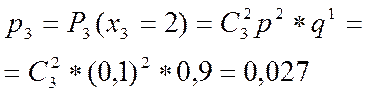
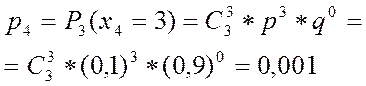
Проверим (3.1)
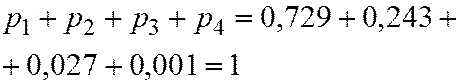
Запишем ряд распределения ДСВ
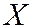
| ||||
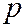
| 0,729 | 0,243 | 0,027 | 0,001 |
Построим многоугольник распределения (схематично):

Построим функцию распределения. Если 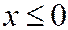 , то
, то 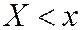 - невозможное
- невозможное
событие и 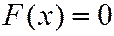
Если  , то
, то 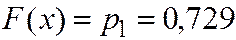 т.к. событие
т.к. событие 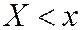 равнозначна событию
равнозначна событию 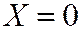
Если 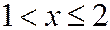 , то
, то 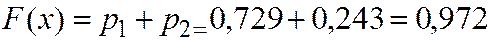 событие
событие 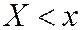 может быть осуществлено, когда
может быть осуществлено, когда 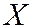 примет значение
примет значение 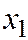 или
или 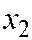 .
.
Поскольку события 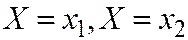 - несовместны и независимы, то
- несовместны и независимы, то 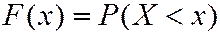 равна сумме вероятностей
равна сумме вероятностей 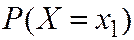 и
и 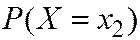 .
.
Если 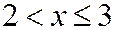 то
то
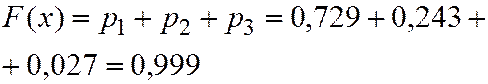
Если 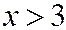 , то
, то 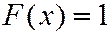 , т.к. событие
, т.к. событие 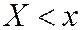 является достоверным.
является достоверным.
Итак
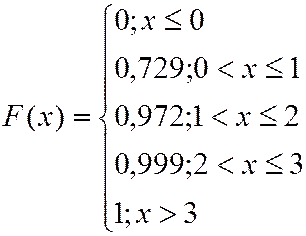
Построим график функции распределения:

Дата добавления: 2015-11-18; просмотров: 875;
