Локальная формула Лапласа

Если число 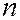независимых испытаний достаточно велико, а вероятность 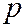появления события 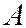в каждом испытании постоянна и отлична от нуля и единицы, а так же 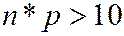, то вместо (2.22) используют асимптотическую локальную формулу Лапласа

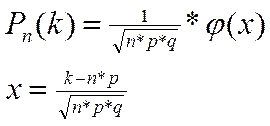, (2.25)

.

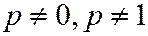Функция 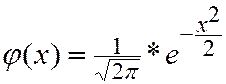называется функцией Гаусса и имеет свойства:

- четности ;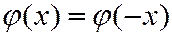

- если 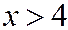, то ;

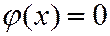- табулирована на отрезке .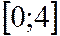

Пример. В партии резисторов 75% изделий не имеют дефектов. Из партии случайным образом отбирают 400 резисторов. Вычислить вероятность того, что 290 штук среди отобранных не будет иметь дефектов.

Решение.

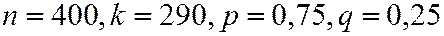
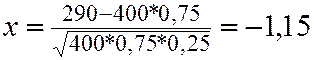
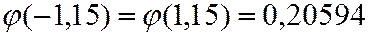
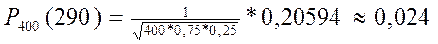
Интегральная формула Лапласа

Вероятность того, что событие 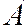произойдет в 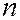независимых испытаниях от 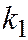до 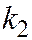раз, есл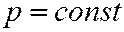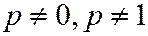и , и 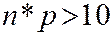, вычисляется по формуле

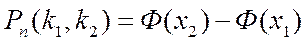, (2.26)

,

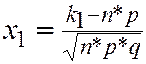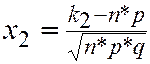
Функция 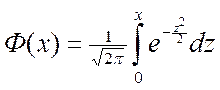называется функцией Лапласа и обладает свойствами:

- нечетности ;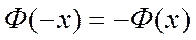

- если 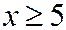, то ;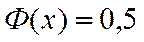

- монотонно возрастает (если 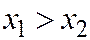, то );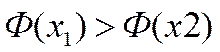

- табулирована на отрезке .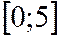

Пример.Для условия предыдущего примера вычислить вероятность того, что среди отобранных резисторов не менее (не более) 290 штук не будут иметь дефектов.

Решение.

,

,

,

,

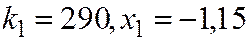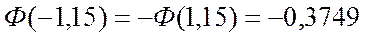
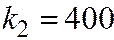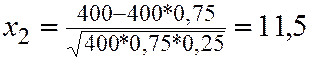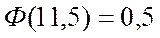
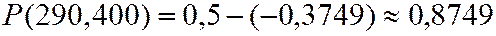
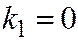
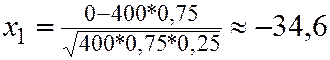
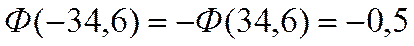
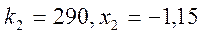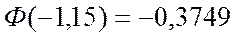
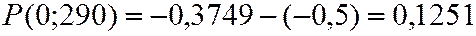
Случайные величины

Общие сведения

Случайнойназывается величина, которая в результате испытания примет одно и только одно из своих возможных значений, заранее неизвестное.

Обозначают случайные величины большими буквами, а их возможные значения – соответствующими малыми буквами. Например, 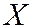- случайная величина, 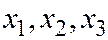ее возможные значения.

Различают случайные величины

-дискретные;

-непрерывные.

Дискретнойназывается случайная величина, которая с определенными вероятностями принимает конечное или бесконечное число отдельных, изолированных возможных значений.

Непрерывной СВназывается СВ, которая может принимать все (бесконечно много) значения из некоторого конечного или бесконечного промежутка.

Случайная величина будет полностью описана с вероятностной точки зрения, если известен ее закон распределения.

Закон распределения случайной величины –это всякое соотношение, устанавливающее связь между всеми возможными значениями этой величины и соответствующими им вероятностями.

Формы представления закона распределения случайной величины:

1) ряд распределения;

2) многоугольник распределения;

3) аналитическая формула;

4) функция распределения;

5) плотность распределения.