Интегральная функция распределения двумерной СВ
Интегральной функцией распределения двумерной СВ ( 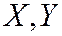 )называют функцию
)называют функцию  , определяющую для каждой пары чисел
, определяющую для каждой пары чисел 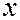 и
и 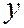 вероятность того, что
вероятность того, что 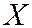 примет значение меньше
примет значение меньше 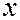 , и при этом
, и при этом  примет значение меньше
примет значение меньше 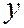
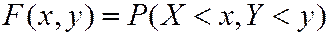 . (4.1)
. (4.1)
Другими словами  - вероятность совместного выполнения двух неравенств
- вероятность совместного выполнения двух неравенств 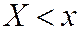 и
и 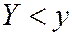 .
.
Геометрически 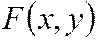 есть вероятность попадания случайной точки
есть вероятность попадания случайной точки 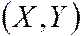 в бесконечный квадрант с вершиной
в бесконечный квадрант с вершиной 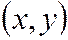 , расположенный левее и ниже этой вершины.
, расположенный левее и ниже этой вершины.

Свойства 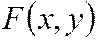 :
:
1.Значения 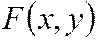 удовлетворяют двойному неравенству
удовлетворяют двойному неравенству
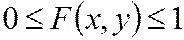
2. 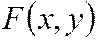 есть неубывающая функция по каждому аргументу, т.е.
есть неубывающая функция по каждому аргументу, т.е.
 если
если 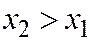
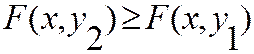 если
если
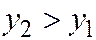
3.Имеют место предельные соотношения

4.При 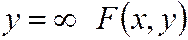 становится интегральной функцией составляющей
становится интегральной функцией составляющей 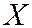

При 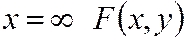 становится интегральной функцией составляющей
становится интегральной функцией составляющей 
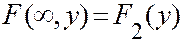
Используя 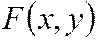 можно определить вероятность попадания случайной точки
можно определить вероятность попадания случайной точки 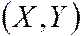 в некоторую область.
в некоторую область.
Если вид области полуполоса

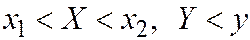


то вероятность попадания в неё (полуполосу) равна приращению 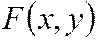 по одному из аргументов
по одному из аргументов
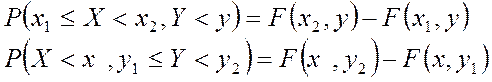 (4.2)
(4.2)
Если вид области – прямоугольник

то вероятность попадания
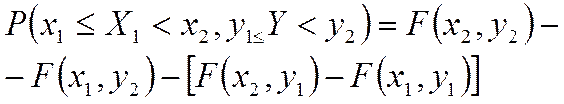 (4.3)
(4.3)
Пример.Двумерная СВ задана 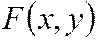

Найти вероятность того, что СВ примет значение из квадрата, вершины которого имеют координаты 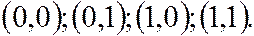
Решение.
Множество точек заданного квадрата определяется соотношением
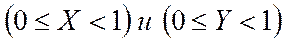
тогда
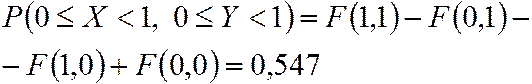
Дата добавления: 2015-11-18; просмотров: 1007;
