Дифференциальная функция распределения непрерывной двумерной СВ
Дифференциальная функция распределения непрерывной двумерной СВ (плотность распределения непрерывной двумерной СВ, двумерная плотность вероятностей)  - это вторая смешанная производная от функции распределения
- это вторая смешанная производная от функции распределения
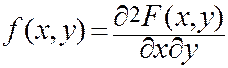 (4.4)
(4.4)
или (что следует из определения производной)  - это предел отношения вероятности попадания случайной точки в элементарный участок плоскости, примыкающий к точке
- это предел отношения вероятности попадания случайной точки в элементарный участок плоскости, примыкающий к точке 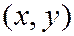 , к площади этого участка, когда его размеры стремятся к нулю.
, к площади этого участка, когда его размеры стремятся к нулю.
Поверхность, изображающая функцию  называется поверхностью распределения.
называется поверхностью распределения.
Интегральная функция 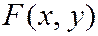 выражается через
выражается через  формулой
формулой
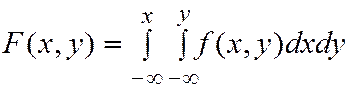 (4.5)
(4.5)
Величина 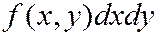 называется элементом вероятности для системы двух СВ и равна вероятности попадания случайной точки
называется элементом вероятности для системы двух СВ и равна вероятности попадания случайной точки  в элементарный прямоугольник со сторонами
в элементарный прямоугольник со сторонами 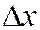 ,
, 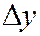 , примыкающий к точке
, примыкающий к точке 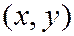 .
.
Вероятность попадания случайной точки  в произвольную область
в произвольную область 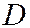 определяется формулой
определяется формулой
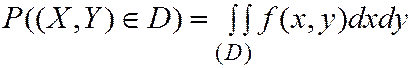 (4.6)
(4.6)
Для прямоугольной области
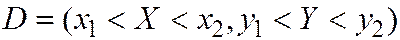

Свойства  :
:
1.  есть неотрицательная функция
есть неотрицательная функция 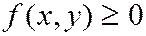 .
.
2. Двойной несобственный интеграл с бесконечными пределами от  равен 1
равен 1

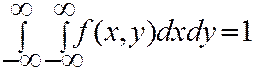
Если все возможные значения  принадлежат конечной области
принадлежат конечной области 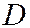 , то
, то

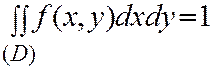
Плотности отдельных величин, входящих в систему двух СВ, можно вычислить через совместную плотность 
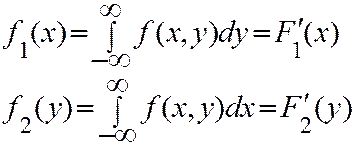 (4.7)
(4.7)
Пример. Система двух СВ  подчинена закону распределения с плотностью
подчинена закону распределения с плотностью
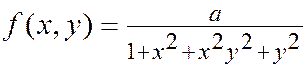
Найти коэффициент 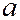 ,
, 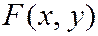 , вероятность попадания случайной точки
, вероятность попадания случайной точки  в квадрат, центр которого совпадает с началом координат, а стороны имеют длину равную 2.
в квадрат, центр которого совпадает с началом координат, а стороны имеют длину равную 2.
Решение.
Из условия 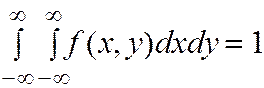 находим
находим
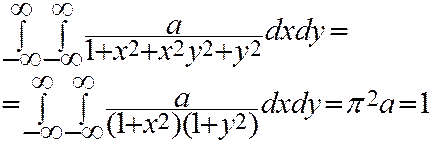
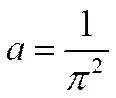
Из формулы (4.5)
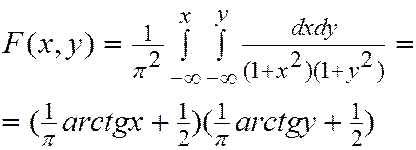
По (4.6) 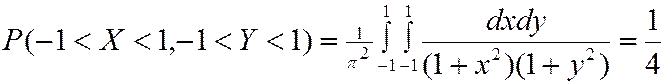
4.3 Числовые характеристики системы двух СВ
Математическое ожидание системы двух СВ  :
:
- для дискретной 
 (4.8)
(4.8)
- для непрерывной 
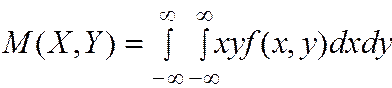
Математическое ожидание составляющих 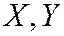 системы двух СВ
системы двух СВ  :
:
- если 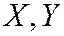 - ДСВ
- ДСВ
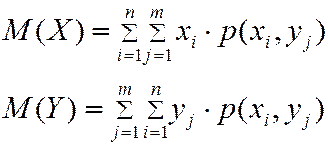 (4.9)
(4.9)
- если 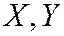 - НСВ
- НСВ
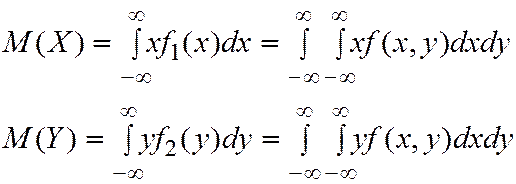 (4.10)
(4.10)
Дисперсия системы двух СВ  :
:
- для дискретной 
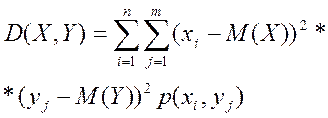 - для непрерывной
- для непрерывной 

| (4.11) |
Дисперсия составляющих 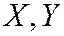 системы двух СВ
системы двух СВ  :
:
- если 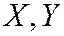 - ДСВ
- ДСВ
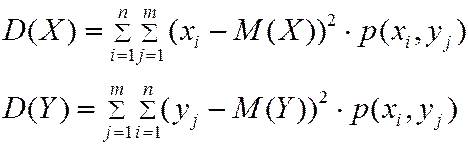 (4.12)
(4.12)
- если 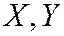 - НСВ
- НСВ
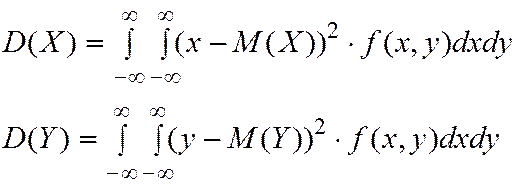 (4.13)
(4.13)
Начальный момент 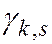 порядка
порядка 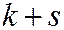 системы двух СВ
системы двух СВ  - МО произведения
- МО произведения 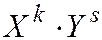 :
:
- для дискретной 
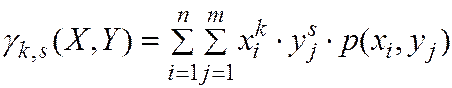 (4.14)
(4.14)
- для непрерывной 
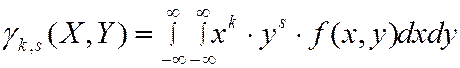
В частности  ,
, 
Центральный момент 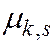 порядка
порядка 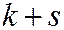 системы двух СВ
системы двух СВ  - МО произведения отклонений соответственно
- МО произведения отклонений соответственно 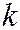 -ой и
-ой и 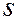 -ой степеней:
-ой степеней:
- для дискретной 
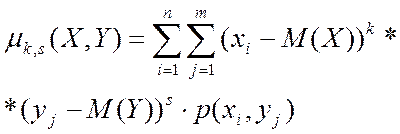 - для непрерывной
- для непрерывной 
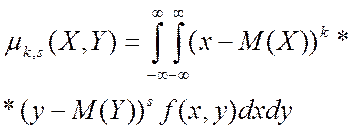
| (4.15) |
В частности
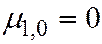 ,
, 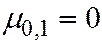 ,
,
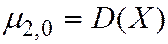 ,
, 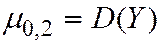
Для характеристики связи между СВ 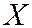 и СВ
и СВ  системы двух СВ
системы двух СВ  служит смешанный центральный момент порядка
служит смешанный центральный момент порядка  , который получил название корреляционный момент (или ковариация)и обозначается
, который получил название корреляционный момент (или ковариация)и обозначается  .
.
Для дискретной  : :
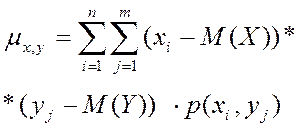 Для непрерывной
Для непрерывной  : :
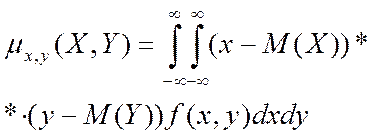
| (4.16) |
Абсолютная величина  не превышает среднего геометрического
не превышает среднего геометрического 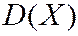 и
и 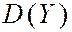
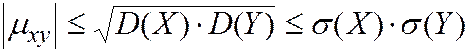
Размерность  равна произведению размерностей СВ
равна произведению размерностей СВ 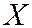 и
и 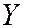 .
.
Для характеристики связи между СВ 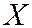 и СВ
и СВ  системы двух СВ
системы двух СВ  независимо от выбора единиц измерения СВ
независимо от выбора единиц измерения СВ 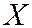 и
и  служит коэффициент корреляции
служит коэффициент корреляции 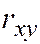 , равный отношению
, равный отношению  к произведению СКО
к произведению СКО 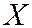 и СКО
и СКО 
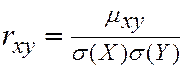 (4.17)
(4.17)
или
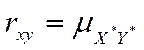 , где
, где

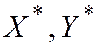 - нормированные СВ с МО=0 и СКО=1.
- нормированные СВ с МО=0 и СКО=1.
Абсолютная величина 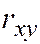 не превышает единицы
не превышает единицы 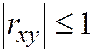 .
.
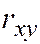 есть величина безразмерная. Коэффициент корреляции
есть величина безразмерная. Коэффициент корреляции 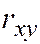 характеризует степень тесноты линейной зависимости между СВ
характеризует степень тесноты линейной зависимости между СВ 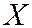 и СВ
и СВ  . Если Х и Y связаны линейной функциональной зависимостью вида
. Если Х и Y связаны линейной функциональной зависимостью вида 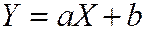 , где
, где 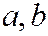 не случайны, то
не случайны, то 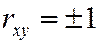 , где знак «+» или «-» берется в соответствии со знаком коэффициента
, где знак «+» или «-» берется в соответствии со знаком коэффициента 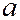 .
.
Пример. Для дискретной двумерной СВ  , заданной таблично
, заданной таблично 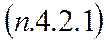 рассчитать числовые характеристики.
рассчитать числовые характеристики.
Решение.
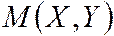 по (4.8)
по (4.8)
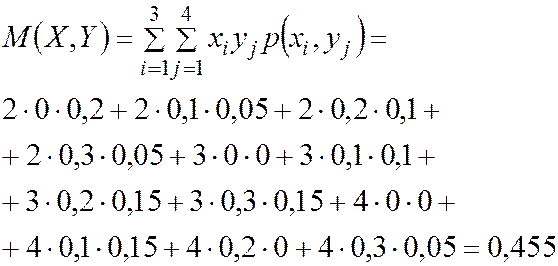
 и
и 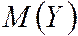 по (4.9)
по (4.9)
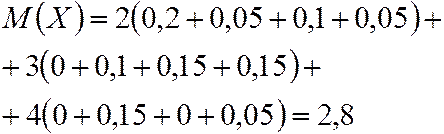
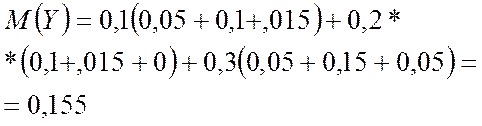
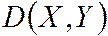 по (4.11)
по (4.11)
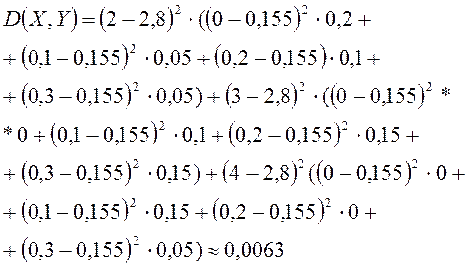
 и
и 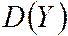 по (4.12)
по (4.12)
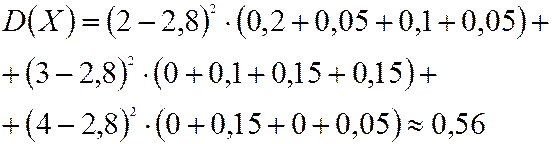
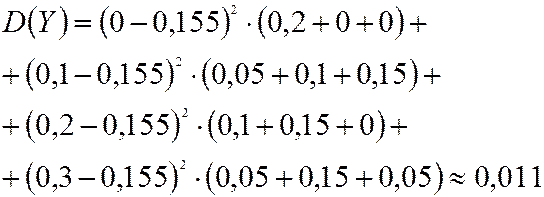
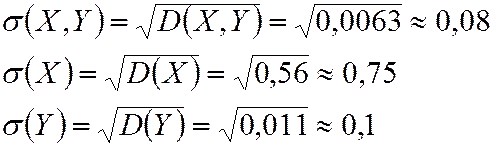
 по (4.16)
по (4.16)
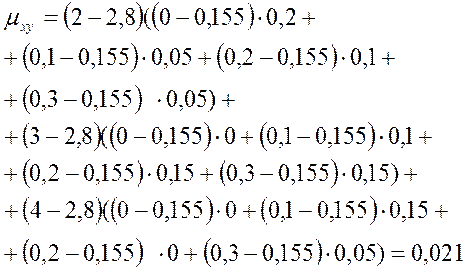
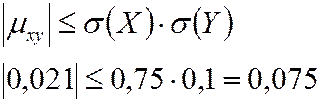 верно
верно
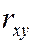 по (4.17)
по (4.17)
 верно.
верно.
Дата добавления: 2015-11-18; просмотров: 856;
