Статистическое распределение выбоки
Пусть из генеральной совокупности извлечена выборка, причем x1 наблюдалось n1 раз, x2 – n2 раз, …, xk – nk раз.
Наблюдаемые значения xi, 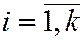 называются вариантами, последовательность вариант, записанная в возрастающем порядке – вариационным рядом.
называются вариантами, последовательность вариант, записанная в возрастающем порядке – вариационным рядом.
Числа наблюдений ni, 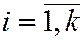 называются частотами, сумма частот составляет объём выбоки
называются частотами, сумма частот составляет объём выбоки
 , (5.1)
, (5.1)
где n – объём выборки,
а отношение ni к n – относительными частотами
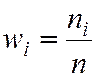 . (5.2)
. (5.2)
Статистическим распределением выборки называют перечень вариант в возрастающем порядке и соответствующих им частот или относительных частот. Статистическое распределение можно также записать в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).
Статистическое распределение можно представить:
1) таблично;
2) графически;
3) аналитически.
Табличное представление статистического распределения имеет вид таблицы, первый ряд которой содержит вариационный ряд или последовательность интервалов, второй – перечень соответствующих частот или относительных частот.
| xi | x1 | x2 | … | xk |
| ni | n1 | n2 | … | nk |
| xi | x1 | x2 | … | xk |
| wi | w1 | w2 | … | wk |
| xi –xi+1 | x1 –x2 | x2 –x3 | … | xk –xk+1 |
| ni | n1 | n2 | … | nk |
Графическое представление статистического ряда распределения может иметь вид:
1. Полигона, если вариационный ряд дискретный;
2. Гистограммы, если вариационный ряд интегральный.
Полигоном частот называется ломаная, отрезки которой соединяют точки (x1; n1), (x2; n2), …, (xk; nk) в декартовой системе координат, где на оси абсцисс откладывают варианты xi, а на оси ординат – соответствующие им частоты ni.
Полигон относительных частот – ломаная, отрезки которой соединяют точки (x1; w1), (x2; w2), …, (xk; wk) в декартовой системе координат, где на оси абсцисс откладывают варианты xi, а на оси ординат – соответствующие им частоты wi.
Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной
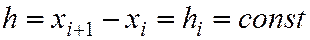 ,
,
а высоты равны отношению  , т. н. плотность частоты.
, т. н. плотность частоты.
Площадь i-го частичного прямоугольника равна ni, площадь гистограммы частот – объекту выборки n.
Гистограмма относительных частот ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению 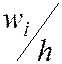 , т. н. плотность относительной частоты.
, т. н. плотность относительной частоты.
Площадь i-го частичного прямоугольника равна wi, площадь гистограммы относительных частот – единице.
Аналитическое представление статистического распределения выборки называется эмпирической функцией распределения.
Эмпирическая функция распределения – функция  , определяющая для каждого значения x относительную частоту события
, определяющая для каждого значения x относительную частоту события 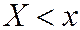 .
.
 , (5.3)
, (5.3)
где nx – число вариант, меньших x ,
n – объём выборки.
Свойства  :
:
1. Значения  принадлежат отрезку [0; 1];
принадлежат отрезку [0; 1];
2.  – неубывающая функция;
– неубывающая функция;
3. Если x1 – наименьшая варианта, то 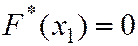 при
при 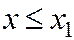 . Если xk – наибольшая варианта, то
. Если xk – наибольшая варианта, то  при
при 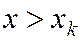 .
.
График  называется кумулятой.
называется кумулятой.
Пример 1. Из 100 транзисторов в среднем бывает два бракованных. Проверили десять партий по 100 транзисторов в каждой. Отклонение количества бракованных транзисторов от среднего заданы таблицей
| Номер партии | ||||||||||
| Отклонение | -1 | -1 | -2 |
Составить закон распределения выборки и построить её эмпирическую функцию распределения.
Закон распределения заданной выборки имеет вид:
| xi | -2 | -1 | |||
| ni | |||||
| wi | 0,1 | 0,2 | 0,2 | 0,4 | 0,1 |
Наименьшая варианта равняется -2, следовательно,
 если
если 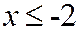 .
.
Значение  , а именно
, а именно 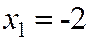
наблюдалось 1 раз, следовательно
 если
если 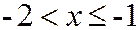 .
.
Значение 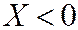 , а именно
, а именно 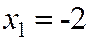 ,
, 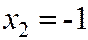 наблюдалось 1+2=3 раза, следовательно
наблюдалось 1+2=3 раза, следовательно
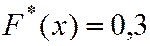 если
если 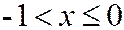 .
.
Значение  , а именно
, а именно 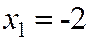 ,
, 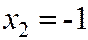 ,
,  наблюдалось 1+2+2=5 раз, следовательно
наблюдалось 1+2+2=5 раз, следовательно
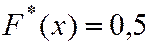 если
если  .
.
Значение 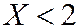 ,а именно
,а именно 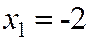 ,
, 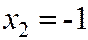 ,
,  ,
,  наблюдалось 1+2+2+4=9 раз, следовательно
наблюдалось 1+2+2+4=9 раз, следовательно
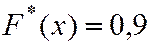 если
если 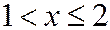 .
.
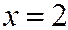 – наибольшая варианта, следовательно,
– наибольшая варианта, следовательно,
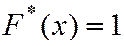 если
если 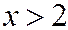 .
.
Искомая эмпирическая функция распределения имеет вид

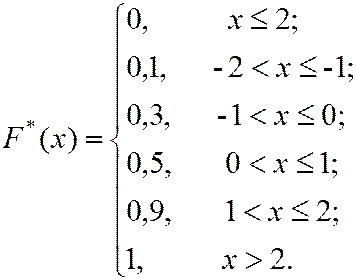
Пример 2.Построение гистограммы частот выборки рассмотрен в учебнике В. Е. Гмурман « Теория вероятностей и математическая статистика», стр. 196.
.
Дата добавления: 2015-11-18; просмотров: 1293;
