Виды статистических гипотез

Статистическойназывается гипотеза (предположение) о генеральной совокупности, которая проверяется на основании выборочных данных.

Статистические гипотезы делятся на:

- гипотезы о виде предполагаемого распределения;

- гипотезы о предполагаемой величине параметра известного распределения.

Пример.

1. Генеральная совокупность распределена по закону Пуассона.

2. Дисперсии двух нормально распределённых генеральных совокупностей равны между собой.

Статистические гипотезы также разделяют на:

- нулевую (основную) H₀, в качестве которой выступает выдвинутая гипотеза;

- конкурирующую (альтернативную) H₁,в качестве которой выступает гипотеза, противоречащая H₀.

Пример.

H₀ состоит в предположении, что математическое ожидание a нормального распределения равно 10, тогда H₁, в частности, может состоять в предположении .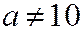

Классификация статистических гипотез выполняется и по количеству предположений в ней:

- гипотеза, содержащая одно предположение, называется простой;

- гипотеза, которая состоит из конечного или безконечного числа простых гипотез, называется сложной.

Пример:

1. Если распределение нормальное, 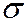– известно, то гипотеза a=3 является простой.

2. Если распределение нормально, 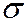– неизвестно, то гипотеза a=3 является сложной.

Основная гипотеза H₀ может быть правильной или неправильной. Т. к. вывод о правильности гипотезы H₀ выполняется по результатам выборки, то всегда существует риск принять неправильное решение. Таким образом, в результате могут быть допущены ошибки двух родов:

- ошибка первого рода (риск производителя), состоящая в том, что будет отвергнута H₀, когда она правильная;

- ошибка второго рода ( риск покупателя), состоящая в том, что будет принята H₀, когда она неправильная.

Вероятность совершить ошибку первого рода принято называть уровнем значимости и обозначать 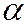. Наиболее часто 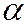принимают равным 0,05 или 0,01.

Вероятность совершить ошибку второго рада обозначают через 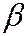, вероятность того, что не будет допущена ошибка второго рода равна 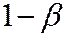и называется мощностью критерия.