Числовые характеристики выборки
Числовые характеристики выборки – параметры выборки, выражающие наиболее существенные особенности статистического распределения выборки.
Выборочной средней 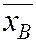 называют среднее арифмитическое значение признака выборочной совокупности.
называют среднее арифмитическое значение признака выборочной совокупности.
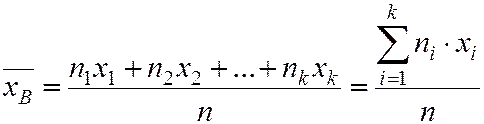 (5.4)
(5.4)
Если статистическое распределение выборки задано интервальным вариационным рядом, тогда при вычислении 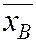 необходимо перейти к дискретному вариационному ряду, вариантами которого выступают середины интервалов
необходимо перейти к дискретному вариационному ряду, вариантами которого выступают середины интервалов
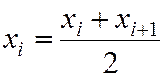 (5.5)
(5.5)
Модой Мо называют варианту, которая имеет наибольшую частоту.
Для интервального статистического распределения сначала определяют модальный интервал [xm; xm+1), для которого 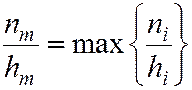 ,
,
где hi – длина частичного интервала [xi; xi+1),
ni – число вариант этого интервала.
Далее
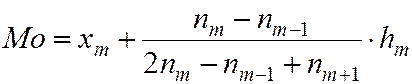 (5.6)
(5.6)
Медианой Ме дискретного статистического распределения называют варианту, которая делит вариационный ряд на две части, равных по числу вариант.
Если число вариант нечётное, то 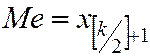 ,
,
если чётное, то
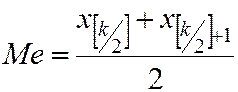 (5.7)
(5.7)
Медианой Me интервального статистического распределенияназывается число, для которого выполняется равенство
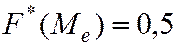 .
.
Формула для вычисления Me имеет вид
 ,
,
(5.8)
где [xm; xm+1) – медианный частичный интервал, для которого выполняется неравенство
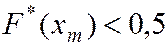 и
и 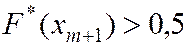 .
.
Дисперсия выборки (выборочная дисперссия) Dв – среднее арифмитическое квадратов отклонений наблюдаемых значений признака от их среднего значения 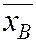 .
.
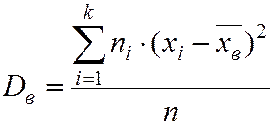 . (5.9)
. (5.9)
Вычисление Dв можно упростить, используя следующую формулу
 . (5.10)
. (5.10)
Dв характеризует рассеяние наблюдаемых значений количественного признака вокруг своего среднего значения 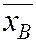 .
.
Выборочным средним квадратическим отклонением (стандартом) 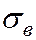 называют квадратный корень из Dв.
называют квадратный корень из Dв.
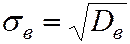 . (5.11)
. (5.11)
Размахом варьирования R называют разность между наибольшей и наименьшей вариантами.
 . (5.12)
. (5.12)
Размах варьирования является простейшей характеристикой рассеяния вариационного ряда.
Средним абсолютным отклонением 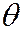 называют среднее арифметическое абсолютных отклонений
называют среднее арифметическое абсолютных отклонений
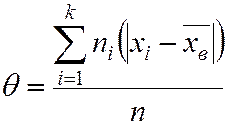 . (5.13)
. (5.13)
Среднее абсолютное значение используется для характеристики рассеяния вариационного ряда.
Коэффициентом вариации V называют выраженное в процентах отношение 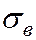 к
к 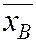 .
.
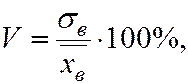 (5.14)
(5.14)
где 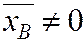 .
.
Коэффициент вариации V служит для сравнения величин рассеяния по отношению к 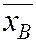 двух вариационных рядов, даже если варианты имеют различную размерность.
двух вариационных рядов, даже если варианты имеют различную размерность.
Сводными характеристиками статистических распределений выступают статистические (эмпирические) моменты.
Обычным эмпирическим моментом порядка l называют среднее значение l-х степеней разностей 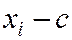 .
.
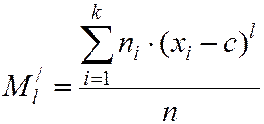 , (5.15)
, (5.15)
где с – произвольная постоянное число, т. н. ложный нуль.
Начальным эмпирическим моментом порядка l называют обычный момент порядка l при с=0.
 . (5.16)
. (5.16)
В частности
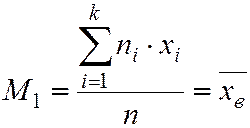 ,
,
т. е. начальный эмпирический момент первого порядка равен выборочной средней.
Центральным эмпирическим моментом порядка l называют обычный момент порядка l при  .
.
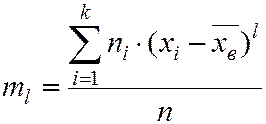 . (5.17)
. (5.17)
В частности
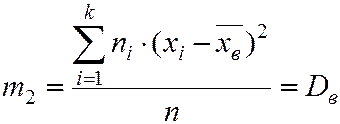 ,
,
т. е. центральный эмпирический момент второго порядка равен выборочной дисперсии.
Центральные моменты можно выразить через обычные:
 ;
;
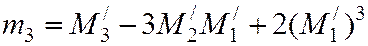 ; (5.18)
; (5.18)
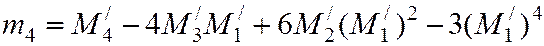 .
.
Условным эмпирическим моментом порядка l называют начальный момент порядка l, вычисленный для условных вариант.
 , (5.19)
, (5.19)
где ui – условная варианта.
Условными называют варианты, определяемые равенством
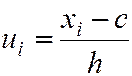 , (5.20)
, (5.20)
где с – любая варианта xi, которая располагается в середине вариационного ряда или является модой;
h – шаг, т. е.
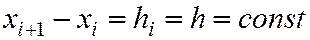 .
.
Таким образом, для вариационного ряда, состоящего из равноотстоящих вариант с шагом h, условные варианты есть целые числа.
В частности

Отсюда
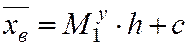 . (5.21)
. (5.21)
Выразим обычные моменты через условные:
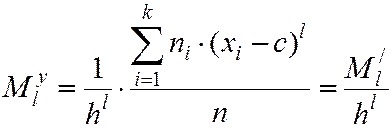 .
.
Тогда
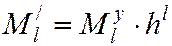 . (5.22)
. (5.22)
Подставив (5.22) в (5.18), можно получить удобные для вычислений формулы, выражающие центральные моменты через условные.
Например, для m2:
 . (5.23)
. (5.23)
Пример. Для статистического распределения рассчитать числовые характеристики.
| xi | |||
| ni |
Решение.
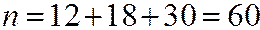 .
.
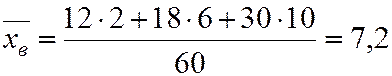 .
.
 .
.
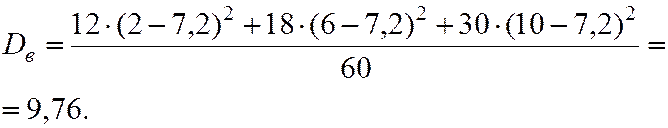 Или
Или
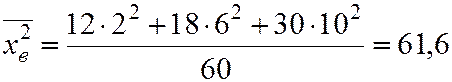 .
.
 .
.
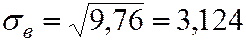 .
.
 .
.

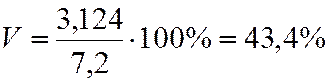 .
.
Перейдём к условным вариантам.
с=10.
| ui | -2 | -1 | |
| ni |
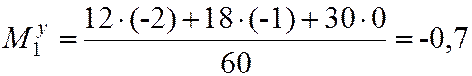 .
.
 .
.
 .
.
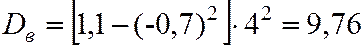 .
.
Теория оценок
Теория оценок определяет методы и способы статистической оценки неизвестных параметров теоретического распределения случайной величины по совокупности экспериментальных данных. При этом часто допускается, что закон распределения генеральной совокупности известен, но неизвестны параметры этого закона (математическое ожидание, дисперсия), которые необходимо оценить (приближённо найти) по выборочной совокупности.
Статистической оценкой неизвестного параметра теоретического распределения называется функция от выборочных значений (вариант), которая даёт приближённое значение оцениваемого параметра.
Все оценки делятся на точечные и интервальные.
Точечные оценки.
Точечнойназывается оценка, которая определяется одним числом.
К точечным оценкам предъявляются следующие требования:
- несмещённости;
- эффективности;
- состоятельности.
Пусть 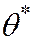 – статистическая оценка неизвестного параметра
– статистическая оценка неизвестного параметра 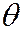 теоретического распределения. Допустим, что по выборке объёма n найдена оценка
теоретического распределения. Допустим, что по выборке объёма n найдена оценка  . Извлечём из генеральной совокупности другую выборку объёма n и вычислим.
. Извлечём из генеральной совокупности другую выборку объёма n и вычислим.  . Повторяя опыт многократно, получим числа
. Повторяя опыт многократно, получим числа  ,
,  ,…,
,…,  , которые, вообще говоря, различны между собой. Таким образом, оценку
, которые, вообще говоря, различны между собой. Таким образом, оценку 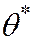 можно рассматривать как случайную величину, а числа
можно рассматривать как случайную величину, а числа  ,
,  ,…,
,…,  – как её вложенные значения.
– как её вложенные значения.
Несмещённой называют статистическую оценку 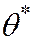 , математическое ожидание которой равно оцениваемому параметру
, математическое ожидание которой равно оцениваемому параметру 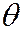 при любом объёме выборки, т. е.
при любом объёме выборки, т. е.
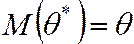 .
.
Смещённой называют оценку, математическое ожидание которой не равно оцениваемому параметру, т. е.
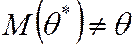 .
.
Эффективной называют статистическую оценку, которая при заданном объёме выборки n имет наименьшую возможную дисперсию.
Состоятельной называют статистическую оценку, которая при 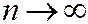 стремится по вероятности к оцениваемому параметру, т. е.
стремится по вероятности к оцениваемому параметру, т. е.
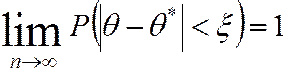 ,
,
где 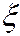 – бесконечно малая величина.
– бесконечно малая величина.
Оценка генеральной средней выборочной средней 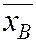 выполняется по формуле (5.4) и является немещённой и состоятельной, если выборка повторная и несмещённой, если выборка бесповторная.
выполняется по формуле (5.4) и является немещённой и состоятельной, если выборка повторная и несмещённой, если выборка бесповторная.
В качестве оценки генеральной дисперсии принимают исправленную выборочную дисперсию S2.
 (5.24)
(5.24)
или
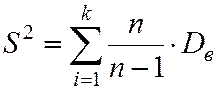 ,
,
которая удовлетворяет требованию несмещённости. Очевидно, при достаточно больших значениях n Dв и S2 различаются мало. На практике S2 вычисляется, если n < 30.
Для оценки среднего квадратического отклонения генеральной совокупности используется исправленное выборочное среднее квадратическое отклонение S или выборочное среднее квадратическое отклонение 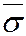 .
.
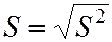 . (5.25)
. (5.25)
Все рассмотренные оценки (формулы (5.4), (5.11), (5.24), (5.25)) являются точечными.
Точечные оценки используются прежде всего тогда, когда с их помощью выполняются другие расчёты. При этом точечные оценки не несут информации о точности конкретной оценки. При малых объёмах выборки точечные оценки могут значительно отличаться от оцениваемого параметра.
Дата добавления: 2015-11-18; просмотров: 3543;
