Интервальные оценки
Интервальной называется оценка, которая определяется двумя числами – началом и концомм интервала, в котором находится оцениваемый параметр теоретического распределения с некоторой вероятностью.
Пусть найденная по данным выборки статистическая оценка 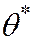 является оценкой неизвестного параметра
является оценкой неизвестного параметра 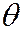 . Статистическая оценка
. Статистическая оценка 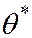 тем точнее определяет параметр
тем точнее определяет параметр 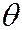 , чем меньше абсолютная величина разности
, чем меньше абсолютная величина разности 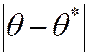 , т. е., если
, т. е., если 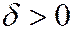 и
и
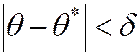 , (5.26)
, (5.26)
то чем меньше 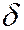 , тем оценка точнее. Таким образом, величина
, тем оценка точнее. Таким образом, величина 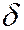 характеризует точность оценки.
характеризует точность оценки.
Т. к. 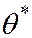 – случайная величина, то нельзя категорически утверждать, что
– случайная величина, то нельзя категорически утверждать, что 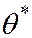 удовлетворяет неравенству (5.26). Вероятность
удовлетворяет неравенству (5.26). Вероятность 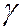 , с которой выполняется неравенство (5.26) называется надёжностью (доверительной вероятностью).
, с которой выполняется неравенство (5.26) называется надёжностью (доверительной вероятностью).
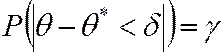 . (5.27)
. (5.27)
Обычно 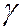 задаётся наперёд в виде числа, близкого к единице, наиболее често – 0,95; 0,99; 0,999.
задаётся наперёд в виде числа, близкого к единице, наиболее често – 0,95; 0,99; 0,999.
Заменим неравенство в формуле (5.27) равносильным двойным неравенством:
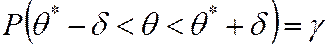 .
.
Интервал 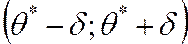 называют доверительным, его границы – доверительными границами.
называют доверительным, его границы – доверительными границами.
Доверительный интервал покрывает неизвестный параметр 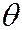 с надёжностью
с надёжностью 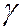 .
.
Если случайная величина X распределено нормально с математическим ожиданием равным a и среднеквадратическим отклонением известным и равным 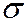 , то по выборке объёма n можно найти доверительные границы для математического ожидания a по уровнениям
, то по выборке объёма n можно найти доверительные границы для математического ожидания a по уровнениям
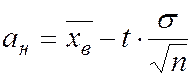 ;
;
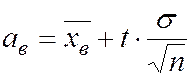 , (5.28)
, (5.28)
где aн и aв – нижняя и верхняя доверительные границы математического ожидания a;
t – коэффициент, определяемый по таблице функции Лапласа, которому соответствует значение функции Лапласа 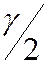 . В этом случае
. В этом случае
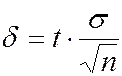 . (5.29)
. (5.29)
Анализ формулы (5.29) показывает, что
- при возрастании объёма выборки n число 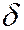 убывает и, следовательно, точность оценки возрастает;
убывает и, следовательно, точность оценки возрастает;
- при увеличении надёжности 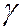 возрастают значения t (функция
возрастают значения t (функция 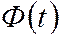 является возрастающей) и
является возрастающей) и 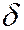 , что приводит к уменьшению точности оценки;
, что приводит к уменьшению точности оценки;
- если требуется оценить математическое ожидание с наперёд заданной точностью 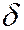 и надёжностью
и надёжностью 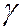 , то минимальный объём выбоки, который обеспечит эту точность находят по формуле
, то минимальный объём выбоки, который обеспечит эту точность находят по формуле
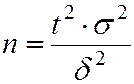 . (5.30)
. (5.30)
Формула (5.30) используется для повторной выборки, для бесповторной выборки минимальный объём пересчитывают по формуле
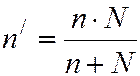 , (5.31)
, (5.31)
где N – генеральной совокупности.
Пример 1. Случайная величина X имеет нормальное распределение с известным среднеквадратическим отклонением 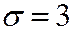 . Найти доверительный интервал для оценки неизвестного математического ожидания a по
. Найти доверительный интервал для оценки неизвестного математического ожидания a по 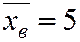 , если
, если  и
и 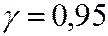 .
.
Решение.
При условии
 ;
;
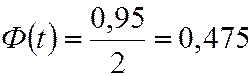 ;
;
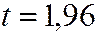 .
.
Вычисляем
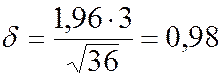 .
.
Получили искомый доверительный интервал:
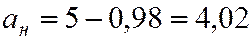 ;
;
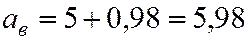 .
.
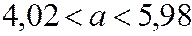 .
.
Пример 2. Найти минимальный объём повторной и бесповторной выборок для генеральной совокупности с объёмом N=1000 с 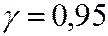 , при котором точность оценки математического ожидания нормально распределённого признака будет равна 0,2 при
, при котором точность оценки математического ожидания нормально распределённого признака будет равна 0,2 при 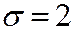 .
.
Решение.
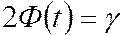 ;
;
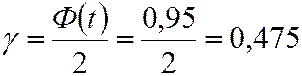 ;
;
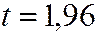 ;
;
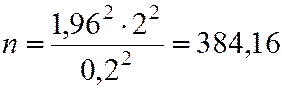 .
.
Принимаем объём повторной выборки n=385.
Для бесповторной выборки
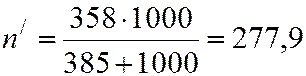 .
.
Принимаем объём бесповторной выборки  .
.
Если случайная величина X распределена нормально с математическим ожидание равным a и среднеквадратическим отклонением 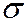 неизвестным, то по выборке объёма n можно найти доверительные границы для математического ожидания a по формулам
неизвестным, то по выборке объёма n можно найти доверительные границы для математического ожидания a по формулам
 ;
;
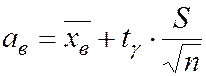 , (5.32)
, (5.32)
где S – исправленное среднеквадратическое отклонение;
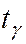 – коэффициент Стьюдента, который определяется по таблице в зависимости от надёжности
– коэффициент Стьюдента, который определяется по таблице в зависимости от надёжности 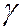 и числа степеней свободы, равное
и числа степеней свободы, равное 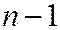 .
.
При неограниченном возрастании объёма выборки n распределение Стъюдента стремится к нормальному, поэтому при n>30 в формулах (5.32) 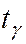 можно заменить на
можно заменить на 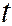 .
.
Если случайная величина X распределена нормально и среднеквадратическое отклонение 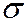 неизвестно, то оценить его помжно по исправленному среднеквадратическому отклонению S, рассчитанному для выборки объёма n, по формулам
неизвестно, то оценить его помжно по исправленному среднеквадратическому отклонению S, рассчитанному для выборки объёма n, по формулам
 ;
;
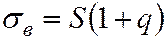 , (5.33)
, (5.33)
где  ,
, 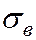 – нижняя и верхняя доверительные границы среднеквадратического отклонения
– нижняя и верхняя доверительные границы среднеквадратического отклонения 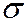 ;
;
q – коэффициент распределения 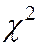 , определяемый по таблице в зависимости от
, определяемый по таблице в зависимости от 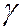 и объёма выборки n.
и объёма выборки n.
Если q<1, то учитывая, что 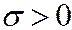 ,
,  .
.
Пример. Случайная величина X имеет нормальное распределение. По выборке объёма n=10 найдено исправленное среднеквадратическое отклонение S=0,16. Найти доверительный интервал, покрывающий неизвестное среднеквадратическое отклонение 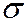 с надёжностью
с надёжностью 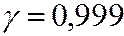 .
.
Решение.
По таблице найдём q=1,8 (q>0) при 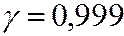 и n=10.
и n=10.
Искомые доверительные границы доверительного интервала:
 ;
;
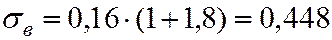 .
.
Практическое применение формулы (5.28) и (5.32) получили для оценки истинного значения измеряемой величины, формулы (5.33) – для оценци точности измерений (точности прибора).
Если случайная величина X имеет биноминальное распределение, то оценить неизвестную вероятность p появления события A в каждом испытании можно, рассчитав доверительные границы по формулам
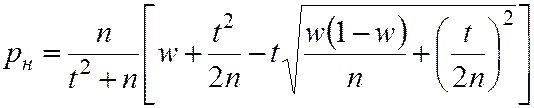 ;
;

где рн и рв – нижняя и верхняя доверительные границы неизвестного значения вероятности p;
w – относительная частота (точечная оценка для p).
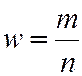 ,
,
где m – число появления события A;
n – число испытаний.
Пример. Производят независимые испытания с одинаковой, но неизвестной вероятностью p появления события A в каждом испытании. Найти доверительный интервал для оценки p с надёжностью 0,95, если в 80 испытаниях событие A появилось 16 раз.
Решение.
По условию m=16, n=80,  .
.
Найдём 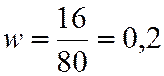 .
.
Найдём t по таблице функции Лапласа из соотношения 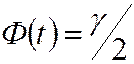 .
.
Подставив n, w, t в формулу (5.34), получим
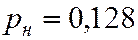 ,
, 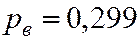 .
.
При больших значениях n (порядка сотен) слагаемые 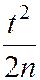 и
и  очень малы и множитель
очень малы и множитель 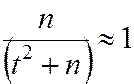 , поэтому доверительные границы можно рассчитать по формулам
, поэтому доверительные границы можно рассчитать по формулам
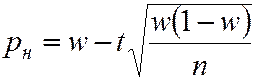 ;
;
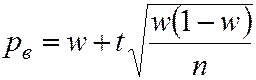 . (5.35)
. (5.35)
Дата добавления: 2015-11-18; просмотров: 1502;
