Проверка статистической гипотезы о параметрах распределения

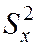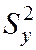Пусть генеральные совокупности СВ X и СВ Y распределены нормально. По независимым выборкам с объёмами, соответственно равными, n₁ и n₂, извлеченным из этих совокупностей, найдены исправленные выборочные дисперсии и . Требуется по 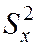и 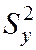при заданном значении 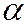проверить, H₀ состоящие в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:

.

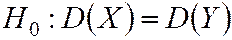В качестве критерия примем отношение большей исправленной дисперсии к меньшей, т. е. СВ F.

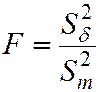. (5.39)

Величина F при условии справедливости H₀ имеет распределение Фишера – Снедекора со степенями свободы

;

,

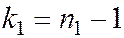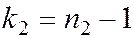где n₁ – объём выборки, по которой вычислена большая исправленная дисперсия;

n₂ – объём выборки, по которой найдена меньшая дисперсия.

Критическую область строят в зависимости от вида конкурирующей гипотезы H₁.

Если 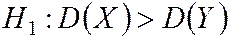, то строят правостороннюю критическую область. Критическую точку F_кр находят по таблице распределения Фишера – Снедекора в зависимости от параметров 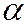, k₁, k₂. Критическая область определяется неравенством F > F_кр, область принятия гипотезы – F < F_кр.

Если 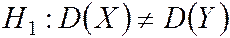, то строят двустороннюю критическую область. Правую критическую точку F_кр2 находят по таблице критических точек распределения Фишера – Снедекора в зависимости по параметров , k₁, k₂.

Левых критических точек эта таблица не содержит. Однако для обеспечения надёжности критерия в двустороннюю критическую область F с уровнем значимости 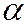, правая критическая точка была определена с доверительной вероятностью . Поэтому критическая область удовлетворяет неравенству F > F_кр2, область принятия гипотезы –

F < F_кр2.

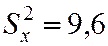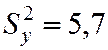Пример. По двум независимым выборкам, объекты которых соответсвенно равны n₁ =10 и n₂ = 15, извлечённым из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии и . При 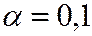проверить 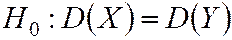при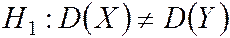

Решение.

Исходя из вида H₁, критическая область – двусторонняя. Определяем F_кр2 пр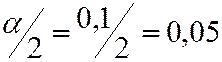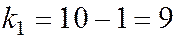и , и .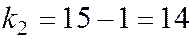

.

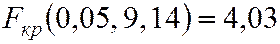Вычисляем по (5.39) .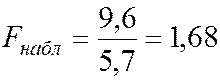

Т. к. 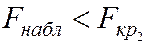, то H₀ не опровергается, дисперсии можно считать равными.