Применение теорем умножения и сложения

На практике сравнительно редко встречаются задачи, в которых нужно применять только теорему умножения или только теорему сложения вероятностей. Обычно эти теоремы приходится применять совместно. При этом, как правило, событие, вероятность которого требуется определить, представляется в виде суммы и (или) произведений нескольких несовместных (совместных) событий.

Пример.По мишени стреляют 3 стрелка. Вероятность попадания для них 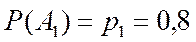, , 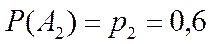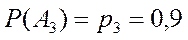. Найти вероятность следующих событий:

B – ни одного попадания;

C – только 1 попадание;

D – только 2 попадания;

E – только 3 попадания;

F – хотя бы одно попадание.

Решение.

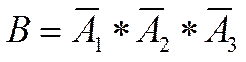
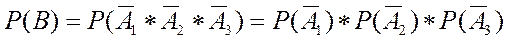по (2.8), т.к. события 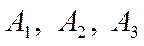- независимы в совокупности.

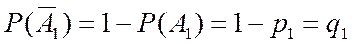по (2.17)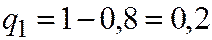

Аналогично

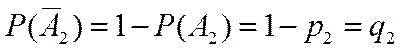
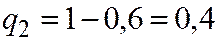
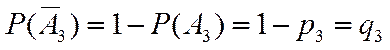
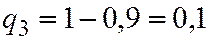
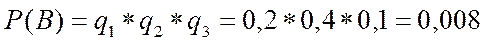
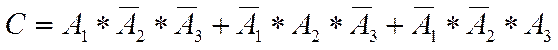
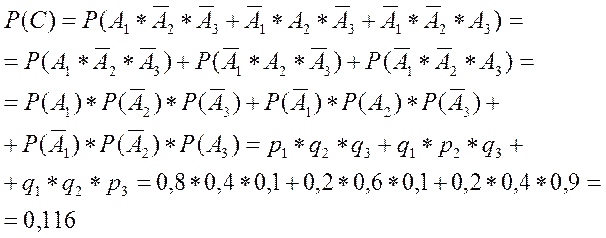
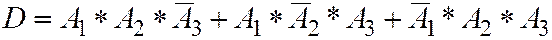
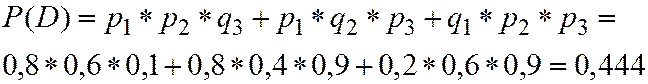
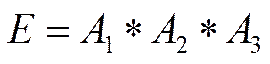
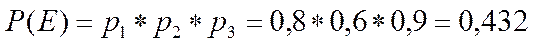
События В, С, D, Е образуют полную группу попарно несовместных событий. Проверим (2.16)

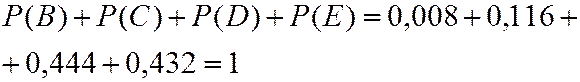
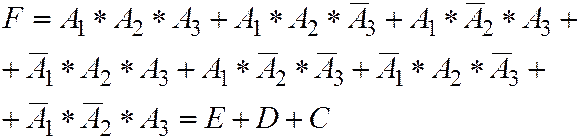
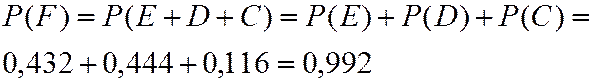
Однако такой путь решения задачи слишком сложен. Здесь проще от прямого события F перейти к противоположному событию – ни одного попадания – что соответствует событию B.

Поэтому

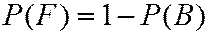
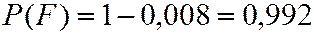
На примере вычисления 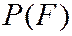проиллюстрирован принцип целесообразности применения противоположных событийв теории вероятностей – если противоположное событие распадается на меньшее число вариантов, чем прямое событие, то имеет смысл при вычислении вероятностей переходить к противоположному событию.