Теорема умножения 1

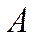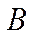Вероятность произведения двух событий и равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило

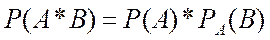, (2.1)

если в качестве первого события взять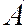

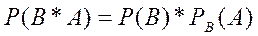, (2.2)

если в качестве первого события взять .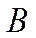

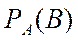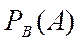, - условные вероятности событи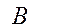й и 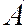соответственно.

Условной вероятностью 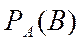называется вероятность события 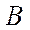, вычисленную в предположении, что событие 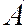уже наступило.

Пример. Студент знает 20 билетов из 30. Он тянет билет шестым. Найти вероятность того, что он сдаст экзамен (событие ), если первых 5 человек вытащили 5 известных ему билетов (событие ).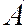

Решение.

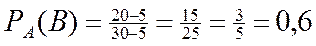
Из формулы (2.1) можно получить формулу для вычисления условной вероятности

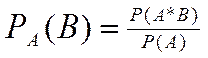(2.3)

Формула (2.3) может быть использована при условии .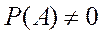

Пример. Проверить формулу (2.3) для предыдущего примера.

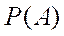находим по (1.7) при , , , .

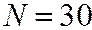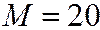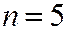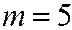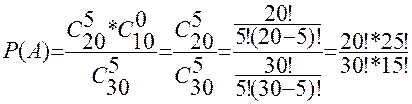
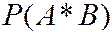определяем по (1.7) при , , , .

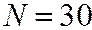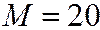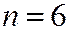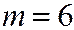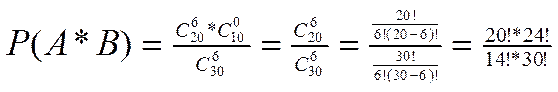
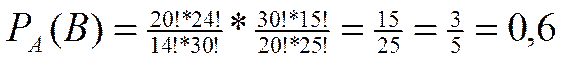
Два события и называются независимыми, если появление одного из них не меняет вероятности появления другого, т.е. условная вероятность события 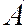равна его безусловной вероятности или, условная вероятность события 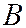равна его безусловной вероятности

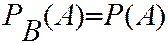(2.4)

.

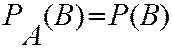Если событие 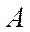не зависит от события 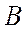, то и событие 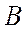не зависит от события .

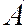Два события 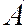и 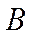являются зависимыми,если

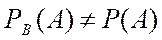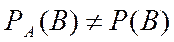или(2.5)

Если событие 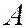зависит от события 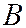, то и событие 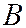зависит от события .

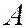Пример.Из полной колоды карт (52 листа) вынимается одна карта. Рассматриваются события

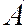- появление туза;

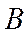- появление карты красной масти;

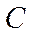- появление бубнового туза;

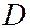- появление десятки.

Зависимы или независимы пары событ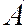и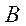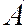й и 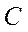, 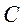и , и ?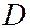

Решение.

Для пары 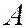и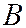

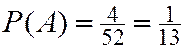
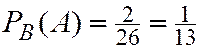
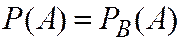
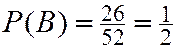
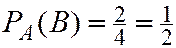
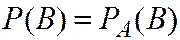
справедливо условие (2.4). Значит и - независимые.

Для пары 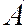и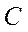

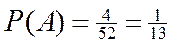
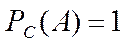
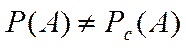
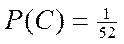
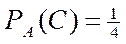
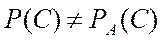
справедливо (2.5). События 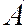и 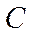зависимы.

Для пары 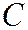и 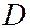, без проверки условий (2.4), (2.5) можно сказать, что события зависимы, т.к. они несовместны. Для несовместных событий (по определению) появление одного исключает появление другого, т.е. обращает в нуль его вероятность.

Несколько событий 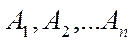называются попарно независимыми,если каждые два из них независимы.

Несколько событий 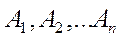называются независимыми в совокупности,если каждые 2 из них независимы и независимы каждое событие и все возможные произведения остальных.