Формулы комбинаторики. Перестановки – комбинации, состоящие из одних и тех же различных элементов и отличающиеся только их порядком.

Перестановки – комбинации, состоящие из одних и тех же 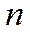различных элементов и отличающиеся только их порядком.

Количество перестановок без повторений

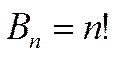(1.2)

Пример:

1. Сколько трехзначных чисел можно образовать из цифр 1, 2, 3, если каждая цифра в числе содержится один раз?

Решение

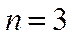- количество цифр

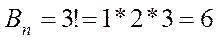
123, 132, 213, 231, 321, 312.

2. Сколько четырехзначных чисел можно образовать из цифр 0, 1, 2, 3 не повторяя их?

Решение.

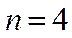(1,2,3,0)

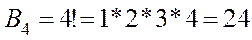
Учитывая, что число с нулем на первом месте является трехзначным, подсчитаем количество таких чисел:

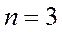(1,2,3)

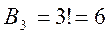
Тогда .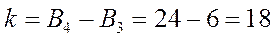

Размещения – комбинации, составленные из 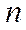различных элементов, взятых по 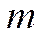элементов, которые отличаются либо составом элементов, либо их порядком.

Число размещений без повторений:

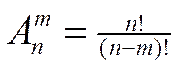(1.3)

Формулы (1.3) и (1.2) связаны между собой формуло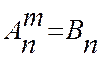й при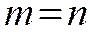

Пример. Сколько различных двузначных чисел можно составить из цифр 1, 2, 3, если цифры в числе не повторяются?

Решение:

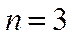
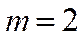
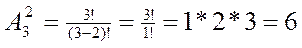
12, 13, 21, 23, 31, 32

Число размещений с повторениями

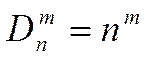(1.4)

Пример. Сколько различных двузначных чисел можно составить из цифр 1, 2, 3, если цифры в числе могут повторяться?

Решение:

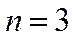
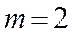
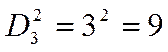
11, 12, 13, 21, 22, 23, 31, 32, 33.

Сочетания – комбинации, составленные из 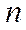различных элементов, взятых по 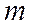элементов, которые отличаются хотя бы одним элементом.

Числовозможных сочетаний безповторений

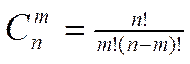(1.5)

Пример. Сколько различных двузначных чисел можно составить из цифр 1, 2, 3, если цифры в числе не повторяются?

Решение:

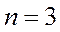
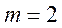
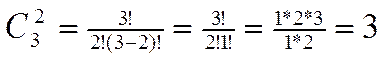
12, 13, 23.

Формулы (1.2), (1.3) и (1.5) связаны между собой следующей формулой

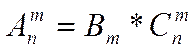(1.6)