Главные движительно-рулевые устройства. 3 страница

 По способу
получения
t и S По способу
получения
t и S
|
 Формуль-ное решение Формуль-ное решение
 дифф. ур. дифф. ур.
|
Численное
решение
 дифф. ур. дифф. ур.

|
 Графичес- кий Графичес- кий
|
 Приближен-ный эмпири-ческий Приближен-ный эмпири-ческий
|

По способу
 ПРЕДСТАВЛЕ-НИЯ ПРЕДСТАВЛЕ-НИЯ
|
Графиков
 V(t) и S(t) V(t) и S(t)
|
Графиков
 S(v) и t(v) S(v) и t(v)
|
Линейных
 графиков
ИМО графиков
ИМО
|
| Таблиц ко- нечных значений S и t |
Рис.1.54. Классификация методов определения тормозных характеристик
В зависимости от способа определения значений коэффициента сопротивления К и максимальной силы упора винта Рmax дифференциального уравнения движения судна различают: расчетный; экспериментальный; экспериментально-расчетный.
Необходимо особо отметить, что решение дифференциальных уравнений торможения будет одинаковым для всех способов определения, различие будет заключаться только в методе получения значений К и Рmax , а также в принятом законе изменения их величин в процессе движения и торможения.
При расчетном методе значения Крас и 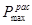 получают путем вычисления по эмпирическим формулам. Точность определения значений параметров по указанным зависимостям характеризуется стандартной относительной погрешностью достигающей 20%. Недостатком расчетного метода является низкая точность получаемых результатов расчетов значений пути и времени торможения.
получают путем вычисления по эмпирическим формулам. Точность определения значений параметров по указанным зависимостям характеризуется стандартной относительной погрешностью достигающей 20%. Недостатком расчетного метода является низкая точность получаемых результатов расчетов значений пути и времени торможения.
Экспериментальный способ определения значений Кэ и 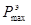 заключается в получении их величин из специально организованных натурных наблюдений.
заключается в получении их величин из специально организованных натурных наблюдений.
Значение Кэ определяется из эксперимента “пассивное торможение”, который рекомендуется выполнять не менее трех раз. Пассивное торможение состоит из двух периодов: 1-й период - время прохождения команды, от момента ее подачи до прекращения подачи топлива ( пара, электричества) на главный двигатель; 2-й период - от момента прекращения подачи топлива до момента, когда скорость упадет до значения 0.2 Vн или потери управляемости, что наступит раньше.
Порядок выполнения эксперимента следующий: дают команду “Стоп”, запускают секундомер, замечают начальную скорость по лагу V0, (если выполняются траекторные измерения то определяют место судна и отсчет лага) и ожидают прекращения подачи топлива (электричества, пара) на главный двигатель; после прохождения команды (оно обычно у ДВС занимает около 10 с., у ГЭУ около 5 с.) замечают скорость, которая обычно не успевает упасть и равна начальной V0, определяют место, записывают отсчет лага и ожидают падения скорости не менее чем наполовину до Vк , удерживая судно на первоначально выбранном курсе. В результате эксперимента получают значения времени tê , têê и пути Sê и Sêê пассивного торможения по периодам и в целом:
tпт = tê + têê , Sпт = Sê + Sêê . ( 1.3. )
Если траекторные измерения выполнены достаточно точно ( со среднеква-дратической погрешностью около 10 м), то определяют значения коэффициента 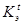 по времени пассивного торможения têê и по пройденному пути
по времени пассивного торможения têê и по пройденному пути 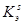 , а результаты осредняют:
, а результаты осредняют:
Кэ = ( 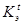 +
+ 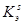 ) / 2 . (1.4. )
) / 2 . (1.4. )
Если эксперимент выполнялся несколько раз, то сначала осредняют значения 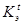 и
и 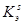 а затем получают значение Кэ .Если же по результатам оценки точности траекторных измерений получено значение ошибки более 10 м, то значение Кэ принимают равным
а затем получают значение Кэ .Если же по результатам оценки точности траекторных измерений получено значение ошибки более 10 м, то значение Кэ принимают равным 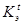 .
.
Значение 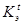 и
и 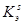 определяют по формулам, полученным из решения дифференциального уравнения пассивного торможения:
определяют по формулам, полученным из решения дифференциального уравнения пассивного торможения:
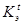 =
= 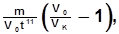 (1.5 )
(1.5 )
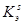 =
= 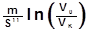 , ( 1.6. )
, ( 1.6. )
где m - масса судна с учетом присоединенной массы воды по оси Х;
V0 - начальная скорость, м/с;
VK - конечная скорость, м/с.
Значение 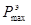 определяют из эксперимента “ активное торможение” задним полным ходом, который рекомендуется выполнять не менее трех раз. Порядок выполнения эксперимента следующий: дают команду ЗП и в момент прохождения стрелки тахометра через “нуль” пускают секундомер, замечают скорость Vн и отсчет лага и определяют место судна; в момент прекращения движения судна останавливают секундомер, определяют место судна и снимают отсчет лага и число оборотов винта. В результате эксперимента получают значения числа оборотов при ЗП, время têêê и путь Sêêê активного торможения при начальной скорости Vн . Если позволяют условия проведения натурных наблюдений, то определение места судна рекомендуется производить через каждые 10-20 секунд. Используя метод последовательных приближений по полученным данным определяют значение
определяют из эксперимента “ активное торможение” задним полным ходом, который рекомендуется выполнять не менее трех раз. Порядок выполнения эксперимента следующий: дают команду ЗП и в момент прохождения стрелки тахометра через “нуль” пускают секундомер, замечают скорость Vн и отсчет лага и определяют место судна; в момент прекращения движения судна останавливают секундомер, определяют место судна и снимают отсчет лага и число оборотов винта. В результате эксперимента получают значения числа оборотов при ЗП, время têêê и путь Sêêê активного торможения при начальной скорости Vн . Если позволяют условия проведения натурных наблюдений, то определение места судна рекомендуется производить через каждые 10-20 секунд. Используя метод последовательных приближений по полученным данным определяют значение 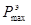 для режима ЗП, которое используется при решении дифференциального уравнения для определения пути и времени активного торможения при различных начальных скоростях.
для режима ЗП, которое используется при решении дифференциального уравнения для определения пути и времени активного торможения при различных начальных скоростях.
Точность экспериментального способа определяется погрешностями траекторных измерений при натурных наблюдениях и обычно позволяет получить наиболее приемлемые для практики судовождения результаты. Его недостатком является невозможность получить данные, для всех возможных скоростей хода и водоизмещения из-за значительной трудоемкости выполняемых испытаний.
Суть экспериментально-расчетного способа определения тормозных характеристик заключается в том, что для значения водоизмещения при эксперименте определяют из натурных наблюдений и рассчитывают величины коэффициентов Кэ и Крас, а также силы упора 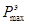 и
и 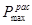 . По полученным значениям определяют переходные коэффициенты gк и gР:
. По полученным значениям определяют переходные коэффициенты gк и gР:
gк =Кэ/ Кр; и 
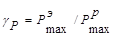 . (1.7. )
. (1.7. )
По значениям указанных коэффициентов для состояния при эксперименте уточняют расчетные значения К и Рmax для произвольного водоизмещения и режима работы главной силовой установки:
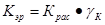 ;
; 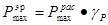 . (1.8. )
. (1.8. )
Использование экспериментально-расчетного способа позволяет получать значение пути и времени торможения с погрешностью менее 10%.
Дифференциальное уравнения движения судна и его решение представляет собой математическую модель торможения. В зависимости от принятого характера изменения сопротивления движению и упора винта при его работе назад от скорости переднего хода различают три основные математические модели - линейная, ЦНИИМФа и ОВИМУ. Сравнительная характеристика указанных моделей приведена в табл.1.1.Из приведенных моделей наибольшей потенциальной точностью обладает модель ОВИМУ. 
Таблица 1.1.
Сравнительная характеристика математических моделей
 Математическая
модель Математическая
модель
| Характер изменения параметров Сопротивления Упора |
| Линейная | K · V Постоянен |
| ЦНИИМФа | K · V2 Постоянен |
| ОВИМУ | K · V2 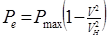
|
К характеристикам поворотливости относятся (рис.6): постоянная времени задержки поворота Т(d ); зона неустойчивости ±w0 , ±dро ; характеристики одерживания поворота tо (d), Qо(d); устойчивость на курсе, критерий Q; выдвиг l1(d); прямое смещение l2(d); тактический диаметр циркуляции Dт(d); диаметр установившейся циркуляции Dу (d); период циркуляции Тц(V,d).
В зависимости от способов определения, получения и представления характеристик поворотливости различают (рис.1.55): по способу определения -экспериментальный, расчетный, экспериментально-расчетный; по способу получения - аналитический и эмпирический; по способу представления данных- в виде графиков и таблиц отрезков, графиков и таблиц перпендикуляров, графиков кривых траекторий ЦТ при циркуляции, таблиц элементов циркуляции.
Экспериментальный способ определения характеристик поворотливости более трудоемок, по сравнению с определением характеристик торможения, поскольку требует более точных способов траекторных измерений и значительной продолжительности по времени их выполнения.
Для получения данных о поворотливости судна предусматривают выполнение следующих маневров: циркуляция; спираль (прямая и обратная); симметричный зигзаг; несимметричный зигзаг.
Программа испытаний и ее объем зависят от того, какие данные о характеристиках поворотливости необходимо получить. Если необходимо получить полное представление о них, то значения скорости и углов перекладки руля определяется количеством характерных точек, которых достаточно для построения надежных зависимостей. Обычно подробный объем испытаний проводят для головных судов серии. Для последующих судов ограничиваются меньшим числом контрольных маневров, позволяющих судить о тождественности маневренных характеристик головного и типового судов.
  Экспери-ментальный Экспери-ментальный
|
 Экспериме-нтально- Экспериме-нтально-
   расчетный расчетный
|
 Расчетный Расчетный
|
 Определения Определения
|

 Получение Получение
|
  Натурные наблюдения Натурные наблюдения
|
  Модельные испытания в бассейнах Модельные испытания в бассейнах
|
  Аналитиче-ские Аналитиче-ские
|
 Эмпириче-ские Эмпириче-ские
|

Представ-
 ление ление
|
 Графиков и таблиц отрезков Графиков и таблиц отрезков
|
| Графиков и таблиц перпендикуляров |
| Таблиц элементов циркуляции |

 Графиков кривых
Графиков кривых
 траекторий ЦТ
траекторий ЦТ
при циркуляции
Рис.1.55. Классификация методов определения характеристик поворотливости
1.4. Силы и моменты, действующие на судно.
Морское судно представляет собой тело, перемещающееся на границе двух сред: воды и воздуха. Поэтому на судно действуют гидро и аэродинамические силы и моменты.
Если же рассматривать килевую, бортовую и вертикальную качки судна, то его движение в горизонтальной плоскости описывается системой из трёх дифференциальных уравнений движения относительно трёх связанных с судном осей: по продольной оси Х, по поперечной оси Y и вокруг вертикальной оси Z. Начало координат расположено в центре тяжести судна, принимаемом обычно на мидель-шпангоуте. Сказанное поясняется на рис.1.56.

В связанной с судном системе координат дифференциальные уравнения, описывающие движение судна в горизонтальной плоскости при ветре имеют вид:
|
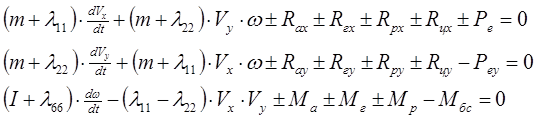
где Ре - сила упора винта;
Реу- боковая сила винта и сила взаимодействия винта и корпуса судна,
Rгх, Raх, Rцх, Rpх - продольные составляющие гидродинамической, аэродинамической, центробежной сил и силы на руле
Rry, Ray, Rцу, Rpy - поперечные составляющие тех же сил.
Mr, Mа, Mбс, Мр - моменты гидро и аэродинамической сил боковой силы винта и руля,
l11,l22,l66,- присоединенная масса по оси X, У и присоединенный момент инерции.
В первых двух уравнениях системы (1.9.) произведения масс на ускорения являются инерционными силами, приложенными к корпусу в центре тяжести и по этой причине они не создают момента относительно центра тяжести. Точно также в третьем уравнении произведение момента инерции на угловое ускорение является инерционным моментом относительно оси Z. При установившемся движении, когда линейные и угловые ускорения равны нулю, инерционные силы и моменты также равны нулю.
На приведённом рисунке(см.рис.1.56.) показан случай движения судна по криволинейной траектории с мгновенным значением радиуса циркуляции, равным R, с центром циркуляции в точке ЦЦ. Инерционные силы на рисунке не показаны.
Почти все силы и моменты, входящие в уравнения системы, выражаются сложными нелинейными зависимостями от поступательной и угловой скоростей и характеристик корпуса движителя и руля, поэтому данная система не может быть проинтегрирована в конечном виде при строгой постановке. Решение возможно только для частных случаев движения и при некоторых упрощающих допущениях. Тем не менее, эта система уравнений позволяет правильно понять и объяснить многие вопросы, связанные с маневрированием судов.
При расчете инерционно-тормозных характеристик используют первое уравнение системы (1.9), которое при прямолинейном движении в отсутствие ветра можно записать так:
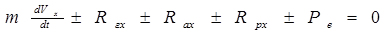 (1.10)
(1.10)
При решении уравнения (1.10) вводят ряд допущений, которые упрощают расчет пути и времени торможения с сохранением точности требуемой нормативными документами Основные из допущений, которые будем использовать в дальнейшем следующие.
1. Присоединенная масса воды по оси Х приближенно равна 10% от массы судна (тх =1,1D) и остается неизменной при маневрировании.
2. Зависимость сопротивления воды и воздуха от скорости носит квадратичный характер
3. Коэффициенты сопротивления воды К и воздуха Ки во время маневрирования постоянны.
4. Упор винта в процессе активного торможения изменяется по зависимости, полученной профессором Деминым С. И.
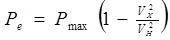 , (1.11)
, (1.11)
где Рmaх - значение силы упора винта в момент остановки; Vx - текущая скорость; Vн - скорость в момент начала вращения винта на задний ход.
5 При маневрировании новое назначенное число оборотов достигает своего значения в момент подачи команды(поскольку двигатель набирает обороты за 5-10 секунд).
Процесс пассивного торможения описывается дифференциальным уравнением:
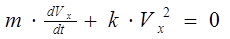 (1.12)
(1.12)
Он имеет два периода - прохождение команды t ' от момента подачи команды "Стоп" до прекращения подачи топлива на главный двигатель (и обычно его принимают равным 10 с) и собственно пассивное торможение t'' - от начальной скорости Vo до конечной скорости Vк, которую принимают равной О.2 Vо или скорости потери управляемости, что наступит раньше (см рис 1.57.) Решение уравнения (1.12) имеет вид:
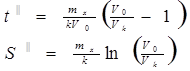 (1.13)
(1.13)



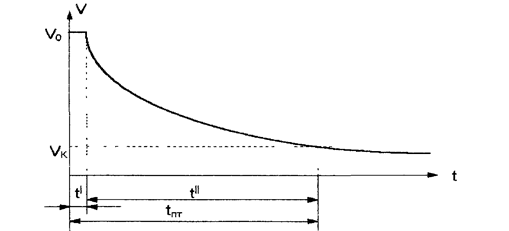
Рис.1.57. График изменения скорости при пассивном торможении
Время и путь пассивного торможения будут равны:
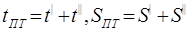 (1.14)
(1.14)
Значение S| рассчитывается по формуле S| = Vo • t|. Информация о пассивном торможении используется при снижении скорости перед началом маневрирования, в случае отказа двигателя и как составная часть активного торможения.
Процессактивного торможения описывается дифференциальным уравнением:
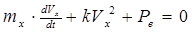 (1.15)
(1.15)
Обозначим коэффициент активности торможения а=Pmax / kV 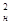 , и с учетом характера изменения силы упора винта, в процессе активного торможения, описываемого формулой (1.11), уравнение (1.15) можно привести к виду, удобному для интегрирования:
, и с учетом характера изменения силы упора винта, в процессе активного торможения, описываемого формулой (1.11), уравнение (1.15) можно привести к виду, удобному для интегрирования:
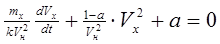 (1.16)
(1.16)
Вид решения уравнения (1.16) зависит от значения коэффициента а.
Изменяющаяся по закону 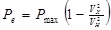 сила упора винта в сумме с силой сопротивления Rx= kV
сила упора винта в сумме с силой сопротивления Rx= kV 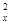 может давать суммарную тормозящую силу как возрастающую при а> 1, так и снижающуюся при а <1. При его значении равном нулю уравнение (1.16) приводится к уравнению (1.12) с соответствующим решением (1.13) и (1.14). При коэффициенте активности торможения а = 1 решение уравнения (1.16) будет иметь вид:
может давать суммарную тормозящую силу как возрастающую при а> 1, так и снижающуюся при а <1. При его значении равном нулю уравнение (1.16) приводится к уравнению (1.12) с соответствующим решением (1.13) и (1.14). При коэффициенте активности торможения а = 1 решение уравнения (1.16) будет иметь вид:
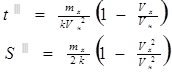 (1.17)
(1.17)
При коэффициенте а < 1 решения уравнения (, с учетом обозначения 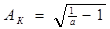 , будут иметь вид:
, будут иметь вид:
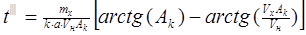 (1.18)
(1.18)
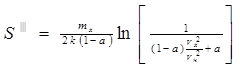 (1.19)
(1.19)
При коэффициенте а > 1 решения уравнения (1.16), с учетом обозначения Вк= 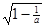 получим:
получим:
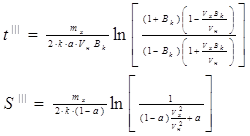 (1.20)
(1.20)
В зависимости от соотношения скорости хода перед началом снижения Vo и скорости уверенного реверсирования Vp, (т.е. скорости при которой главный двигатель уверенно запускается на упор заднего хода), общее время и путь активного торможения будут рассчитываться различным образом (рис. 1.58).
. Время и путь активного торможения можно рассчитать по формулам:
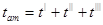 ,
, 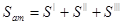 (1.21)
(1.21)
При Vo > Vpeв значение пути первого периода рассчитывают как обычно S 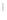 = Vo • t|. Во время второго периода будет происходить пассивное торможение до тех пор, пока скорость не упадет до Vрeв, а расчет пути можно произвести по формуле (1.12), подставляя Vк = Vpeв.
= Vo • t|. Во время второго периода будет происходить пассивное торможение до тех пор, пока скорость не упадет до Vрeв, а расчет пути можно произвести по формуле (1.12), подставляя Vк = Vpeв.







|
|
|
|




 При Vo < Vрев расчет пути первого периода производится аналогично предыдущему случаю, а время второго периода определяется техническими характеристиками главного двигателя и равно времени запуска двигателя на задний ход. Для ДВС, согласно правил технической эксплуатации, оно равно t|| =15 секунд. С учетом этого путь второго периода рассчитывают по формуле S|| = Vo t||.
При Vo < Vрев расчет пути первого периода производится аналогично предыдущему случаю, а время второго периода определяется техническими характеристиками главного двигателя и равно времени запуска двигателя на задний ход. Для ДВС, согласно правил технической эксплуатации, оно равно t|| =15 секунд. С учетом этого путь второго периода рассчитывают по формуле S|| = Vo t||.

Процессразгонаописывается дифференциальным уравнением:
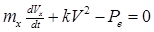 (1.22)
(1.22)
Для упрощения решения дифференциального уравнения (1.22) при переходных режимах необходимо ввести дополнительное допущение, что назначенная сила упора движителя устанавливается мгновенно, в момент подачи команды, и равна новому режиму движения. Такое допущение можно сделать потому, что переходные процессы в двигателях происходят значительно быстрее, чем изменение скорости
По окончании разгона, когда судно будет двигаться с установившейся скоростью Vycт .сила инерции равна нулю, и уравнение (1.22) принимает вид:
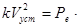 (1.23)
(1.23)
Подставив (1.23) в (1.22) получим дифференциальное уравнение разгона:
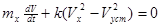 (1.24)
(1.24)
Вид решения уравнения (1.24) зависит от того, из какого начального состояния производится разгон - из неподвижного состояния или от меньшей скорости к большей. В первом случае после разделения переменных в уравнении (1.24) и интегрирования в пределах от 0 до Vx получим выражения для расчета пути и времени разгона:
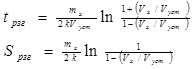 (1.25)
(1.25)
Полученные формулы (1.25) позволяют получить время и путь разгона судна из неподвижного состояния до заданной установившейся скорости. Однако процесс разгона длится достаточно долго ( при Vx ®Vуст tpзг и Spзг стремятся к бесконечности). Для того чтобы разрешить получающуюся неопределенность, будем считать процесс законченным, когда скорость движения Vx достигает 0.95 Vуст. Указанное допущение удовлетворяет практические потребности судовождения, поскольку точность определения места судна и показаний лага в совокупности лежат в указанных пределах. С учетом этого допущения формулы (1.25) для расчета конечных значений пути и времени разгона, упрощаются и принимают вид:
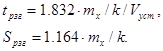 (1.26)
(1.26)
Процессразгона от произвольной скорости V1 до значения Vуст описывается дифференциальным уравнением (1.22),с пределами интегрирования от V1 до Vyст. Тогда формулы для расчета пути и времени разгона принимают вид:

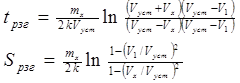 (1.27)
(1.27)
С учетом того, что процесс разгона от скорости V1 до Vycт также длится продол-жительное время, выражения для расчета конечного пути и времени разгона упростятся и принимают вид:

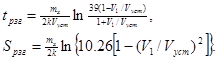 (1.28)
(1.28)
Укажем еще на одну особенность процесса разгона. При нагрузке двигателя от ППм до ПП (или, как еще принято называть в практике судовождения морского хода, - Sea speed) процесс продолжается весьма долго и время его выполнения является технической характеристикой двигателя судна. В зависимости от типа двигателя он длится от 25 до 45 мин. Поэтому при подсчете пути разгона скорость можно считать линейно нарастающей от Ппм до ПП, а путь рассчитать по средней ее величине.
Дата добавления: 2015-11-18; просмотров: 1544;
