Г) Графическая обработка результатов.
Выбор координатных осей. По оси абсцисс всегда откладывается аргумент, по оси ординат – функция.
Выбор масштаба. При выборе масштаба необходимо придерживаться следующих рекомендаций:
1. Шкалы на всех осях должны легко читаться, поэтому одна клеточка миллиметровой бумаги должна соответствовать удобному числу единиц измеряемой величины (1, 2, 5, 10….).
2. Экспериментальные точки не должны сливаться друг с другом.
3. Масштабы вдоль осей следует выбирать так, чтобы основная часть графика имела наклон, близкий к 45º, и лежала в средней части между осями.
4. Если на графике необязательно иметь начало координат, начало, и конец разметки по осям должны соответствовать минимальным и максимальным значениям аргумента и функции.
5. Десятичные множители удобнее отнести к единице измерения, тогда деления на осях будут помечены цифрами 1; 2; 3 и т. д., а не 10000; 20000 или 0,001; 0,002.
Построение графиков. На график наносятся все полученные в измерениях точки (выносные линии не проводятся). Через экспериментальные точки проводится наилучшая плавная кривая. Непосредственное соединение экспериментальных точек ломаной линией не допускается. Точки должны располагаться как можно ближе к кривой так, чтобы по обе стороны от неё находилось по возможности одинаковое число точек.
Нанесение ошибок на график. Ошибка в экспериментальном значении указывается в виде крестиков, размеры которых в выбранном масштабе дают удвоенное значение погрешностей в этом масштабе. Кривая графика должна пересекать прямоугольники, образованные крестиками погрешностей.
Оформление графиков.
| 2∆x |
| 2∆y |
| y |
| x |
Рисунок 1 – Оформление графиков
Каждый график выполняется на миллиметровой бумаге, снабжается заголовком, содержащим точное описание зависимости, показываемой на нём, и вклеивается в отчёт.
д) Основные правила приближенных вычислений.
Значащими цифрами числа называются все его цифры, кроме нуля, если он стоит в начале. Пример: 0,03010 – 4 значащие цифры.
Общее правило – при вычислении сумм, разностей, произведений, частных результат не должен содержать больше значащих цифр, чем наименее точное из слагаемых, сомножителей и т. д.
При вычислении функций ограничиваются числом значащих цифр аргумента. Если результат вычисления является промежуточным и используется в дальнейших вычислениях, необходимо сохранить в нем на одну значащую цифру больше, чем это требуется предыдущим правилом. Если в вычисляемое выражение входят постоянные типа π, γ, константы приборов и т. п., следует для них брать значащих цифр на одну больше, чем в самом неточном из участвующих в выражениях чисел. Это делается для того, чтобы вычисления с постоянными величинами не вносили дополнительные ошибки.
Если это по каким-либо причинам невозможно (например, значения постоянной прибора недостаточно точно известны), то соответствующую константу в выражении для физической величины следует рассматривать наравне с другими переменными, и в окончательное выражение для физической величины будет входить погрешность соответствующей константы.
Абсолютную погрешность следует всегда выражать в тех же единицах измерения, что и саму измеряемую величину. Например, L = (1,572 ± 0,004) м, но не L = (1,572 ± 4) мм. Число и его погрешность всегда записывается так, чтобы их последние цифры принадлежали к одному и тому же десятичному разряду. Нельзя писать 24 ± 0,2, или 21,62 ± 0,3. Правильная запись 24,0 ± 0,2 или 21,6 ± 0,3. Нуль писать так же обязательно, как и любую другую цифру: 25,30 ± 0,02, но не 25,3 ± 0,02.
Приближенные числа рекомендуется представлять в нормальном виде, для чего первая значащая цифра записывается в разряде единиц, а остальные – в разряде десятых, сотых и т.д. Например: 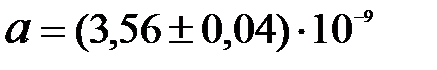 м = (3,56 ± 0,4) нм
м = (3,56 ± 0,4) нм
Вычисленные погрешности прямых и косвенных измерений должны округляться до одной значащей цифры, за исключением тех случаев, когда она равна 1 – в этом случае сохраняется две значащих цифры, причём вторая из них округляется до 5.
При записи констант и других заданных чисел часто применяется неявный способ указания их погрешностей: выписываются только надёжно известные
значащие цифры числового значения, а ненадёжные отбрасываются с применением обычных правил округления. Например, запись L = 1,2 м читается как
L = (1,20 ± 0,05) м и так далее. Иначе говоря, погрешность в этом случае составляет половину невыписанного разряда.
е) Кинематика материальной точки.
Материальной точкой (частицей) называется тело, размерами, структурой и внутренними движениями которого в данных условиях при описании движения можно пренебречь.
Системой отсчёта (СО) называется совокупность тела отсчёта, относительно которого рассматривается движение других тел, линеек и часов. Прежде чем говорить о движении и его описывать, нужно выбрать СО.
Кинематика изучает геометрические формы и типы движений безотносительно к причинам, их вызывающим. Все СО кинематически эквивалентны в смысле возможности выбрать любую из них для описания движения.
Дата добавления: 2015-11-18; просмотров: 1167;
