Основная задача физического измерения состоит в том, чтобы указать интервал, внутри которого с заданной наперёд вероятностью находится истинное значение искомой величины.
Интервал значений величины x, заданный соотношением (3), называется доверительным интервалом, а вероятность Р – доверительной вероятностью или надежностью, соответствующей этому доверительному интервалу.
По способу учёта в лабораторном практикуме погрешности делятся на 4 типа: поправки – ∆ xпопр., погрешности разброса – ∆ xразб., приборные погрешности –
∆ xпр., погрешности отсчёта и округления – ∆ xокр..
Поправки вводятся тогда, когда известна или найдена величина и знак систематической ошибки. Например, если известна неточность градуировки прибора (указана в паспорте или графике поправок),то на неё вводится поправка.
Погрешности разброса учитывают те случайные ошибки, которые приводят к разбросу результатов около некоторого среднего значения при многократном повторении опыта в неизменных условиях.
К погрешностям разброса можно отнести также погрешности, связанные с грубостью принятой математической модели. Например, достаточно точные измерения длины реального стола дадут разные результаты в разных местах, так что если в качестве модели для реального стола принимаем модель прямоугольника с определёнными длиной и шириной, то различие значений длины и ширины в разных местах следует принимать как наличие погрешностей разброса.
Погрешности приборов учитывают неизвестные экспериментатору систематические ошибки конкретного прибора, связанные с его конструктивными особенностями.
Погрешности отсчёта и округления учитывают те случайные ошибки, которые вызваны несовершенством органов чувств экспериментатора и округлением результатов.
Величина погрешности ∆ x (она называется абсолютной) не всегда удобна для характеристики точности измерений и получаемых результатов. Например, если абсолютная погрешность измерения длины 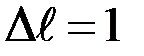 мм, а измеряемая длина составляет несколько метров, то точность измерения хорошая, а если измеряемая длина всего несколько миллиметров, то точность будет уже плохой. В связи с этим, так же из-за неудобства сравнения точности измерения разных величин, например, длины и времени, вводят относительную погрешность измерения, которую обычно выражают в процентах.
мм, а измеряемая длина составляет несколько метров, то точность измерения хорошая, а если измеряемая длина всего несколько миллиметров, то точность будет уже плохой. В связи с этим, так же из-за неудобства сравнения точности измерения разных величин, например, длины и времени, вводят относительную погрешность измерения, которую обычно выражают в процентах.
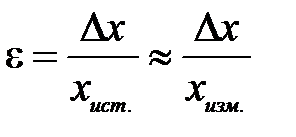 или
или 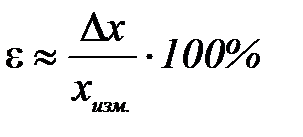 (4)
(4)
Дата добавления: 2015-11-18; просмотров: 1057;
