Кроме измеренного значения физической величины должна указываться и возможная величина ошибки.

Поскольку истинное значение измеряемой величины в формуле (I) неизвестно, неизвестна и ошибка измерения δx. Для измерения возможной величины ошибки δx вводится понятие погрешности ∆ x.

Погрешность ∆ x измерения – это количественная мера неизвестной экспериментатору ошибки измерения δx. Количественно ∆ x можно задать как наибольшую по модулю ошибку так, чтобы выполнялось неравенство:

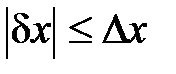(2)

Тогда из (1) и (2) следует, что истинное значение измеряемой величины лежит в интервале:

x_изм. – ∆ x ≤ x_ист. ≤ x_изм. + ∆ x (3)

Опыт, однако, показывает, что нерационально, а часто невозможно выбирать ∆ x столь большим, чтобы равенства (2) и (3) выполнялись абсолютно надёжно. Действительно, чем больше ∆ x, тем менее ценным является результат. Например, результат измерения длины маятника 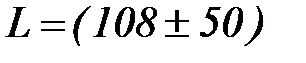см, несомненно, надежней результата 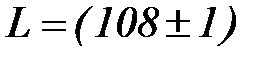см, однако ценность первого результата, конечно, ниже ценности второго. Поэтому величину ∆ x задают так, чтобы неравенства (2) и (3) выполнялись с некоторой вероятностью, Р. В учебных лабораториях принимают Р = 0,95. Это означает, что при многократном повторении опыта в одних и тех же условиях в среднем в 95 случаях из 100 ошибки не превысят ∆ x.