С помощью разрешающего элемента.
Разрешающим элементом матрицы называется всякий ненулевой элемент. Соответственно ему строка и столбец, в котором он расположен, называются разрешающей строкой и разрешающим столбцом. Алгоритм преобразования матрицы с помощью разрешающего элемента состоит в следующем:
○ новые элементы разрешающей строки получаются из соответствующих элементов прежней строки делением на разрешающий элемент.
○ все элементы разрешающего столбца, кроме разрешающего, равны нулю.
○ остальные элементы расширенной матрицы пересчитываются по правилу прямоугольника: если aij – разрешающий элемент, пересчитывается элемент aek расширенной матрицы, то
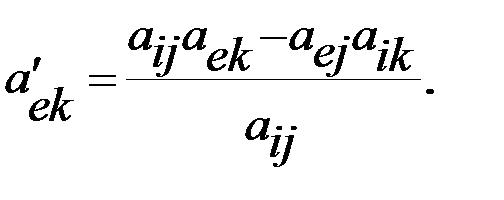
В матрице это выглядит следующим образом:
| ....aij......................aik... .............1..................... .................................... ...........2....................... aej.............................aek |
Нахождение базисных решений, основанное на использовании разрешающего элемента, производится для наглядности с помощью симплексных таблиц, исходным видом которой является запись расширенной матрицы в виде:
| х1 | х2 | … | хn | Свободные члены |
| а11 | а12 | … | a1n | b1 |
| a21 | a22 | … | a2n | b2 |
| … | … | … | … | … |
| am1 | am2 | … | amn | bm |
Последующие шаги получаются перерасчетом ее с использованием разрешающего элемента для превращения ее в ступенчатую матрицу для получения одного (первого) базисного решения. Все они (шаги) помещаются друг за другом в симплексной таблице.
Если математическая модель, представляемая системой линейных алгебраических уравнений, описывает объект, переменные в которой могут принимать и отрицательные значения, то в качестве разрешающего элемента может приниматься элемент с любым знаком.
Большинство задач линейного программирования (для распределения ресурсов, полей под культуры, транспортных средств и др.) имеет дело с неотрицательными переменными, поэтому необходимо уметь находить эти неотрицательные решения изучаемых систем. В этом случае алгоритм нахождения решений (неотрицательных) несколько изменяется:
○ приводим расширенную матрицу к виду, в котором все свободные члены – числа неотрицательные, умножением тех строк на (-1), в которых свободные члены – числа отрицательные;
○ за разрешающий столбец принимается тот, в котором имеется хотя бы один положительный элемент, если такового нет при положительных свободных элементах, то система вырожденна (решений не существует);
○ при наличии в разрешающем столбце нескольких положительных элементов находятся отношения соответствующих свободных элементов к этим положительным элементам, и в качестве разрешающего элемента выбирается тот, для которого это отношение наименьшее;
○ далее осуществляется пересчет таблицы по правилу прямоугольника, данные пересчета рисуются под первой таблицей.
Этот метод расчета носит название симплексного. После симплексного пересчета все свободные члены остаются положительными.
Выбор столбца с наименьшим отношением свободного члена и положительного элемента столбца обусловлен необходимостью создания устойчивости вычисления (меньшего накопления ошибок при использовании приблизительной оценки элементов матрицы), а также соблюдения неотрицательности свободных членов при преобразованиях.
Пример 1. Найти базисные неотрицательные решения системы линейных алгебраических решений.
х1+х2+х3+х4+х5=7
3х1+2х2+х3+х4-3х5= -2
х2+2х3+2х4+6х5=23
5х1+4х2+3х3+3х4-х5=12
После умножения второго уравнения на (-1) получаем исходную запись симплексной таблицы и ее преобразования по описанному алгоритму.
| Базисные переменные | х1 | х2 | х3 | х4 | х5 | bi | Базисные решения |
| -3 | -2 | -1 | -1 | ||||
| -1 | |||||||
| 1/5 | 2/5 | 2/5 | 6/5 | 23/5 | |||
| 2/5 | 4/5 | 4/5 | 12/5 | 46/5 | |||
| 4/5 | 3/5 | 3/5 | -1/5 | 12/5 | |||
| ранг r=2 | |||||||
| C25=10 | |||||||
| х5 | 1/6 | 1/3 | 1/3 | 23/6 | 19/6;0;0;0;23/6 | ||
| х1 | 5/6 | 2/3 | 2/3 | 19/6 | |||
| x5 | -1/5 | 1/5 | 1/5 | 16/5 | 0;19/5;0;0;16/5 | ||
| x2 | 6/5 | 4/5 | 4/5 | 19/5 | |||
| x5 | -1/2 | -1/4 | 9/4 | 0;0;19/4;0;9/4 | |||
| (x4) x3 | 3/2 | 5/4 | 19/4 | 0;0;0;19/4;9/4 |
Максимальное количество базисных решений, как видно из таблицы, 10, но не все сочетания переменных по 2 дают решения. Получено 3 базисных решения. Других нет. Это тоже видно из таблицы. Из последнего ее шага следует, что в качестве разрешающих элементов могут быть выбраны только 3/2 и 5/4, но они приводят к уже найденным решениям, х5 из базисных убрать не представляется возможным.
Пример 2. Найти неотрицательные базисные решения системы линейных алгебраических решений.

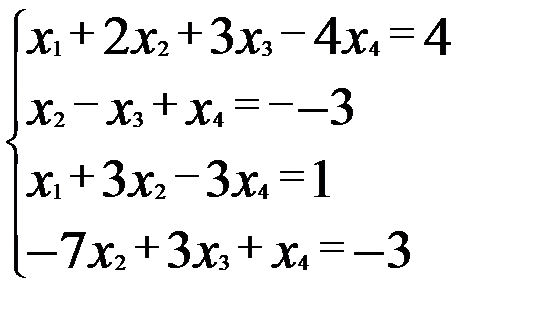
Умножив второе и четвертое уравнения на (-1), получим исходную матрицу симплексной таблицы.
| Базисные переменные | х1 | х2 | х3 | х4 | bi | Базисные решения |
| -2 | -4 | |||||
| -1 | -1 | |||||
| -3 | ||||||
| -3 | -1 | |||||
| 1/3 | -2/3 | -4/3 | 4/3 | |||
| -1/3 | -1/3 | 1/3 | 5/3 | |||
| -3 | ||||||
| -5 | ||||||
| 5/9 | -2 | 14/9 | Базисных неотрицательных решений не существует | |||
| -2/9 | 16/9 | |||||
| 1/3 | -1 | 1/3 | ||||
| -2/3 | 16/3 |
Две равносильных (вторая и четвертая) строки матрицы имеют однозначное решение (отрицательное, х=-8), поэтому система несовместна, а значит, не имеет неотрицательных решений.
Рассмотренные методики решения системы линейных алгебраических уравнений могут быть использованы в расчетах по определению реакций в стержнях, являющихся элементами металлических ферм, расходов жидкости в разветвленных каналах, токов в разветвленных электрических цепях. Самое большое приложение они имеют при оптимизации (отыскании наилучших решений) задач линейного программирования. Особенность применения этих методик в этом случае состоит в необходимости приведения математических моделей линейного программирования к каноническому виду.
Дата добавления: 2015-11-12; просмотров: 2678;
