Методика численного решения обыкновенных дифференциальных уравнений первого порядка.

Различные учебники по решению дифференциальных уравнений много внимания уделяют методам получения первообразных и их последующего исследования, как будто убеждая обучающегося или другого читателя в возможности получения такого решения для большинства из них. Однако, опыт показывает, что большинство практических задач не может быть решено этим методом (т.е. в квадратурах).

Для получения приближенных решений пригодны различные аналитические методы, и перед тем, как перейти к численным методам (наиболее универсальным), надо исследовать и их.

Способность получать решение дифференциальных уравнений в виде аналитических функций («берущиеся» интегралы) это не только наука, но искусство перестраивать, преобразовывать подынтегральные выражения для получения полных дифференциалов каких-то известных функций.

Исследователям-прикладникам часто нужно получить конкретные решения математических моделей в дифференциальном виде, поэтому для них численные решения кажутся более универсальными, хотя и требуют проведения нового этапа преобразования получаемых результатов для создания возможностей проведения оптимизации.

Все численные методы решения дифференциальных уравнений опираются на физическую сущность интегрального исчисления: значение искомой функции в какой-либо точке области определения аргумента равняется сумме значений этой функции в исходной точке и ее приращения на некотором отрезке аргумента. Из математического анализа известно, что при достаточно малом изменении аргумента приращение функции почти равно дифференциалу этой функции на рассматриваемом участке - производной в исходной точке интегрирования, умноженной на элементарное приращение аргумента.

Для численного решения дифференциальных уравнений разработано большое число методов, различающихся по способу вычисления решений и информации, которая используется на каждом шаге расчета.

Решение дифференциального уравнения по шагам основано на разбиении интервала, на котором оно ищется, на части фиксированными значениями независимой переменной. Значение искомого решения в каждой из полученных дискретных точек определяется как функция значений решения в одной или нескольких предыдущих точках, вычисляемая с помощью элементарных операций.

Известно, что значение любой дифференцируемой функции в любой точке интервала через значение этой функции в рядом расположенной точке (в смысле удаления на достаточно малую величину изменения аргумента, сравнимую с бесконечным приближением ее к исходной точке) может быть представлено в виде ряда Тейлора:

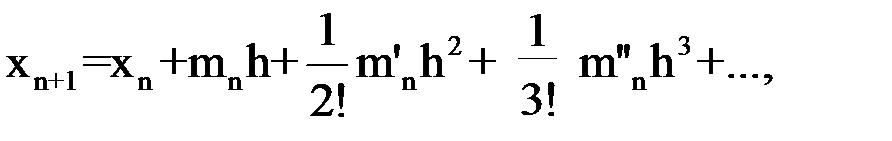
если x_n(t_n) значение функции в рядом расположенной точке (в предыдущей точке разбиения интервала), t_n – значение аргумента в этой точке;

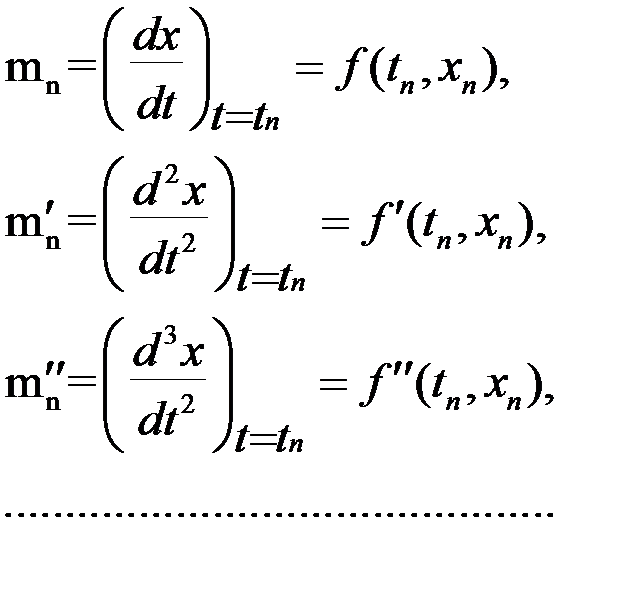
h=(t_n+1-t_n) - шаг разбиения интервала (шаг вычисления).

Для вычисления используется ограниченное число членов ряда, поэтому погрешность полученного значения оценивается с помощью остаточного члена ряда Тейлора:

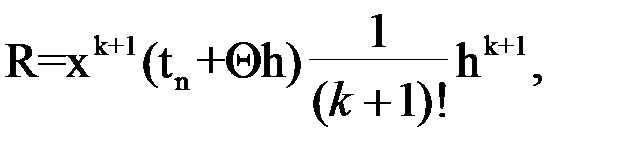
где 0<Θ<1. Ряд сходится довольно быстро (по числу членов использованного ряда).

Для выполнения следующего этапа вычисления x(t_n+2)=x_n+2 выбирают шаг

h=t_n+2-t_n.

При небольшом используемом числе членов ряда Тейлора в вычислениях точность полученного решения снижается. В этих случаях после нескольких шагов расчета по этому алгоритму рекомендуется снова определить значение производной в последней точке и, считая ее исходной, продолжить расчет.

Этот метод оказывается очень трудоемким, поэтому часто применяются другие более простые, но тоже достаточно точные методы. Все они фактически также опираются на использование ограниченного числа членов разложения решения в ряд Тейлора.

4.4.1 Метод Эйлера. Этот метод искомое решение x(t) дифференциального уравнения

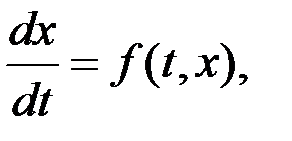
проходящее при t=t₀ через точку x(t)=x₀ (начальное условие), заменяет ломаной из прямолинейных отрезков. Каждый отрезок касается интегральной кривой в одной из своих граничных точек рисунка 4.1.

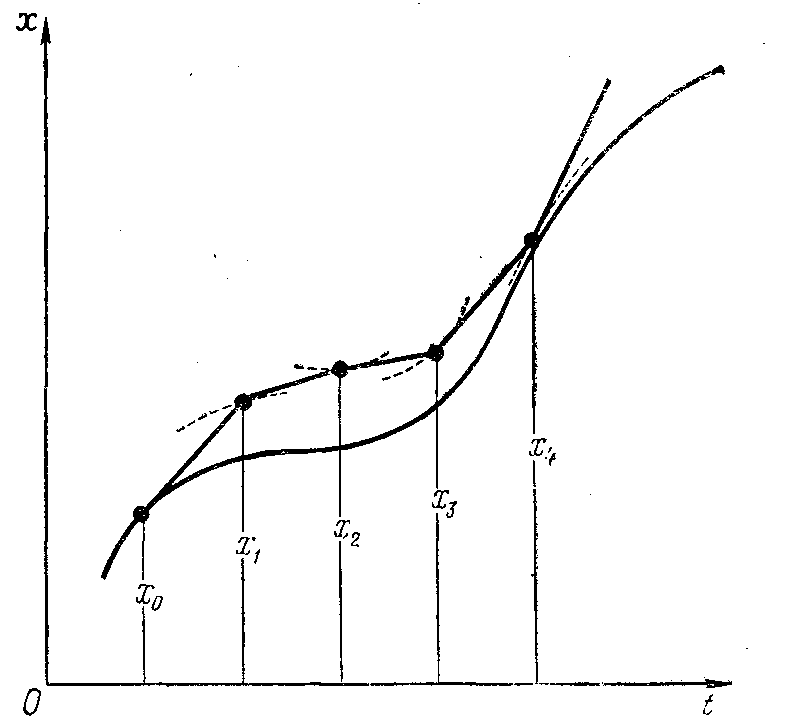
Рис.4.1. Численное решение дифференциального

уравнения методом Эйлера.

Интервал вычисления функции делится на n равных частей точками (t₀,t₁,t₂,...t_n) .Длина каждой из них h=t_i+1-t_i.

Для построения интегральной кривой используется следующий алгоритм счета:

x₁=x₀+hf(t₀,x₀),

x₂=x₁+hf(t₁,x₁),

........................

........................

x_n=x_n-1+hf(t_n-1,x_n-1).

Из представленного графика видно, что уменьшение шага квантования (разбиения) h приближает вычисляемые точки к фактической интегральной кривой. Теоретически доказано, что в пределе при h→0 ломаная стремится к кривой x(t).

Метод Эйлера использует ряд с отбрасыванием членов с h в степени выше первой. Точность его определяется величиной порядка h². Повышение точности достигается уменьшением шага дискретизации (разбиения) h, что увеличивает время счета.

Усовершенствованным методом Эйлера является метод уравнивания. Его алгоритм вычисления будет выглядеть следующим образом:

x_k+1=x_k+hf(t_k,x_k),

x '_k+1=f(t_k+1,x_k+1).

Уточнение x_k+1 -

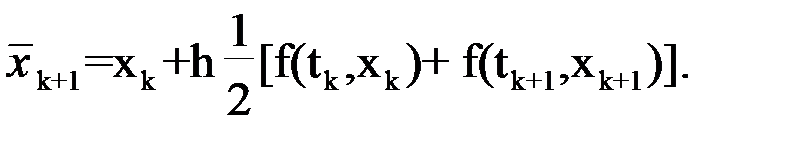
Вместо x'_k в отличие от алгоритма Эйлера берется среднее арифметическое значение производных в точках границ интервала. По полученному значению 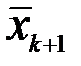вновь уточняют величину производной 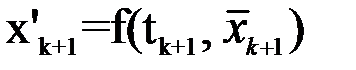и вычисляют более точное приближение функции 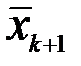по предыдущей формуле. Этот процесс осуществляют до совпадения результатов расчета на предыдущем шаге в пределах заданной точности.

Метод уравнивания имеет погрешность порядка h³. Прямая, которая аппроксимирует искомую функцию, не является касательной к фактической интегральной кривой ни в одной из граничных точек.

4.4 2 Метод Адамса. Искомое решение в этом случае основывается на бóльшем числе членов его разложения в ряд Тейлора. При этом может использоваться увеличенный шаг разбиения. Зато в качестве приближенного решения используется не линейная зависимость от h, а кривая, определяемая алгебраическим уравнением относительно h в степени выше первой.

Но все методы, основанные на таких алгоритмах, фактически являются методами, использующими увеличенное число членов разложения функции в ряд Тейлора за счет корректировки положения касательной к кривой в исходной точке интегрирования. Точность численного решения в этом случае зависит от степени аппроксимирующей кривой, описывающей прирост искомой функции на одном шаге интегрирования.

4.4.3 Метод Рунге-Кутта. Этот метод оказался наиболее приемлемым в практике одношаговых вычислений вследствие использования для получения решения в очередной точке значения искомой функции только в одной предыдущей точке.

Общая формула вычисления решений одношаговыми методами имеет вид:

x_k+1= x_k+hФ_f(t_k,x_k,h),

где Ф_f – функция, зависящая от правой части f(t,x) дифференциального уравнения в форме Коши.

Еще раз подчеркнем, что основное преимущество одношаговых вычислений заключается в том, что приближенное значение решения в точке (t+h) получается на основе информации, полученной в точке t.

Чаще всего в вычислениях используется формула Рунге-Кутта четвертой степени:

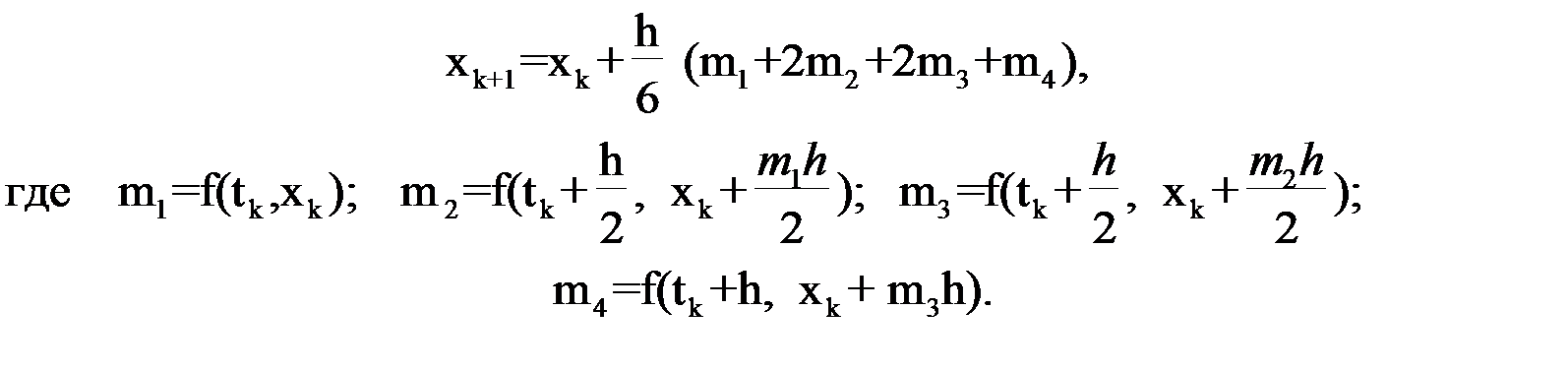Если сравнить получаемое значение по вышеприведенной формуле с разложением искомой функции около точки t_k, x_k в ряд Тейлора, то окажется, что члены со степенями h ниже пятой совпадают, а значит, погрешность вычисления на каждом шаге вычисления будет величиной порядка h⁵.

Метод Рунге-Кутта обладает хорошей точностью и часто используется при решении дифференциальных уравнений с помощью вычислительных машин. Его важным преимуществом является возможность применения переменного шага при вычислениях. Недостаток его заключается в необходимости вычисления f(t,x) в нескольких точках.

44.4 Метод последовательных приближений. При уже использованных нами начальных условиях t=t₀ и x(t₀)=x₀ искомое решение для значений t>t₀ уравнения x'(t)=f(t,x) может быть представлено в виде:

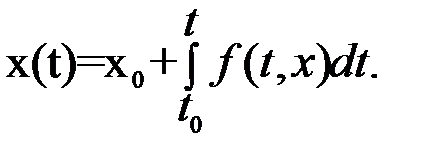
На первом шаге вычисления заменим неизвестную х на х₀ и получим первое приближение: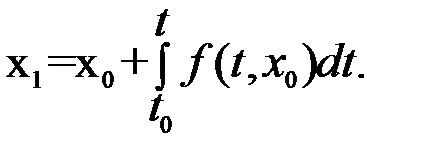

При втором приближении – ,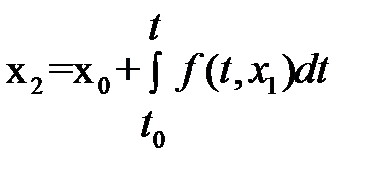

а при n- приближении – .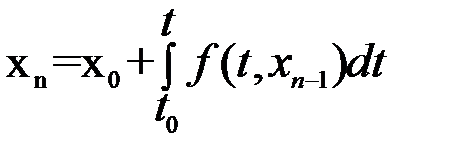

Доказано, что при соответствии условий дифференциального уравнения существованию и единственности решения, решение такого уравнения будет пределом последовательности приближений x_n при n→∞ на некотором достаточно малом отрезке (t₀, t₀+∆t).

Этот метод называется итерационным методом Пикара. Процесс итерации продолжается до тех пор, пока разница в двух последних приближениях не окажется в пределах требуемой точности.

Все рассмотренные выше методы на примере решения уравнения первого порядка легко распространяется на уравнения более высокого порядка. Для этого используется метод приведения их к системе уравнений первого порядка, то есть к нормальной форме Коши.

Рассуждения по поводу решения одного дифференциального уравнения могут быть перенесены и на систему обыкновенных дифференциальных уравнений первого порядка. В связи со сказанным о методе Эйлера с его возможностями уравнивания прироста искомых приращений всех функций правых частей уравнений он может быть перенесен и на решение системы дифференциальных уравнений.

Методы Адамса и Рунге-Кутта практически тоже являются усовершенствованием метода Эйлера увеличением числа членов разложения функции в ряд Тейлора, используемого в вычислениях. Поэтому они также используются в практике численного машинного решения дифференциальных уравнений при одном существенном замечании, если правые части уравнений системы достаточно раз дифференцируемы. Последнее замечание не относится к итерационному методу Пикара, который при расчете приближений использует не дифференциальные, а интегральные приближения.

При использовании приближенных решений дифференциальных уравнений важным является вопрос оценки точности этих решений. Погрешности решений в этом случае складываются из трех частей:

○ погрешности, связанной с неточным выполнением начального условия, т.е. ошибками в определении значения решения в одной или нескольких предыдущих точках;

○ погрешности, появляющейся при аппроксимации решения с ошибкой, пропорциональной h^p+1, убывающей с уменьшением h, где p- наивысшая степень разложения искомой функции в ряд Тейлора при вычислении;

○ погрешности, определяющейся приближениями при вычислениях (округлениями, способом реализации алгоритма в машине), характеризуемой величиной 1/h, которая растет с уменьшением h.

Все эти погрешности имеют тенденцию к росту с увеличением шага вычисления (квантования). Неудовлетворительность строгих оценок приводит к использованию асимптотических оценок, близких к гарантированным пределам погрешности. В машинных расчетах эти оценки используются для автоматического выбора шага квантования при расчетах.

В практике численных расчетов обычно используется следующий прием выбора шага разбиения (квантования) интервала, на котором определяется решение:

○ исходя из ориентировочных оценок погрешности метода (например, учитывая лишь порядок погрешности) выбирается некоторый шаг h;

○ производятся вычисления с шагом h и шагом h/2 и сравниваются результаты расчета в общих точках;

○ если отличие в результатах лежит в пределах заданной точности, то принимается шаг, равным h;

○ в противном случае шаг уменьшается вдвое (h/4) и вновь сравниваются результаты вычислений с шагом h/2 и h/4 и т.д.;

○ различие в результатах счета будет уменьшаться с уменьшением шага до тех пор, пока погрешность округления не станет превалирующей.