Представление результатов эксперимента (любого вычислительного или натурного) поверхностью отклика при оптимизации объектов исследования.
Методику отыскания оптимальных условий поведения объектов исследования, зависящих от многих факторов, обосновали Бокс и Уилсон. Особенность рассматриваемых ими объектов состояла в том, что механизм процессов, осуществляемых в них, в целом неизвестен. Таковыми являются физические, химические и металлургические процессы. К таким объектам могут быть отнесены и те, которые описываются детерминированными связями в зависимости от определяющих их факторов, но многочисленность которых делает эти зависимости неявными.
Методика эта опирается на известную возможность представления получаемых результатов в виде полиномов. Чтобы избежать полиномов высокого порядка, ими был предложен шаговый метод изучения поверхностей отклика, очень похожий на итерационный метод решения задач вычислительной математики. Алгоритм действий исследователя по предложенной методике оптимизации таков:
○ постановка небольшой серии опытов для локального описания малого участка поверхности отклика полиномом первой степени (регрессионным уравнением);
○ движение (расчет в отдельных точках) в самом «крутом направлении» (в направлении самого быстрого роста исследуемого полинома – в направлении градиента линейного приближения);
○ при недостаточности линейного приближения постановка новой серии опытов для линейного описания объекта уже в более ограниченной области изучения;
○ продолжение шагового процесса до тех пор, пока исследователь не попадет в почти стационарную область, где линейное приближение оказывается невозможным;
○ постановка расширенной серии опытов для получения поверхности отклика второго (реже третьего) порядка.
Этот путь приводит довольно быстро к той части поверхности отклика, которая преимущественно интересует исследователя.
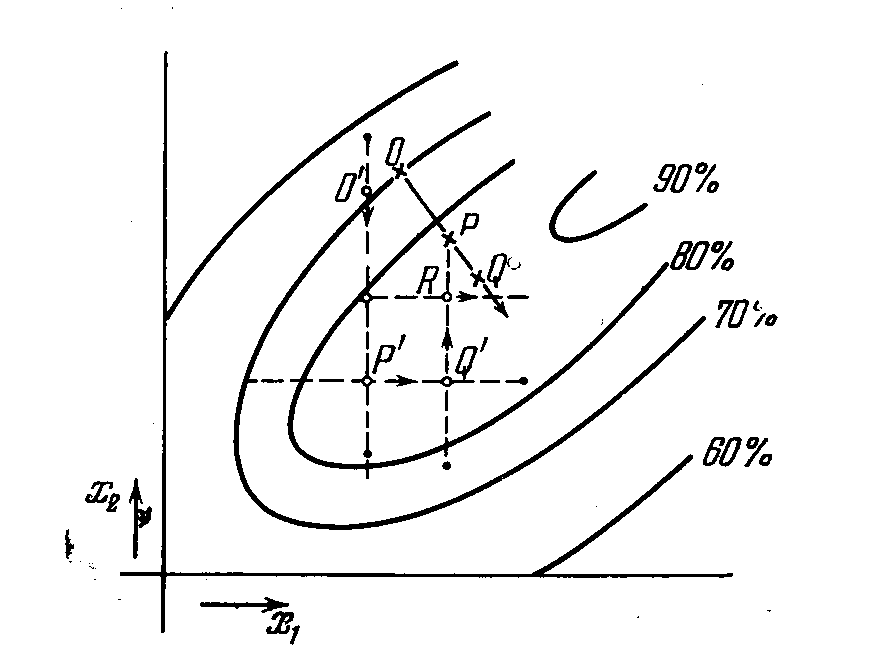
Рис 5.6 Оптимизация объекта методом крутого восхождения
На рисунке (5.6) графически представлено движение по градиенту в задаче с двумя независимыми переменными. На графике показаны линии равного значения параметра оптимизации изучаемого процесса, аналогичные кривым равной высоты на географических картах. Строя согласно математическим правилам нормали к этим кривым, получаем векторные линии градиента скалярного поля, заданного функцией отклика. Движение из точки О в направлении нормали Р соответствует наиболее крутому пути подъема по поверхности отклика (отсюда название метод крутого восхождения). В направлении ОР движение можно продолжать до точки Q. В ее окрестности надо ставить вторую серию опытов для получения нового (локального) линейного приближения поверхности отклика. Ни в какое сравнение с описанным методом не идет оптимизация по однофакторному эксперименту (она похожа на блуждание по лабиринту, о чем свидетельствует линии рисунка).
Оптимизация по методу крутого восхождения была известна и до Бокса. Новым в его работе было использование градиента в сочетании с дробным факторным экспериментом для локального описания поверхности отклика.
При изучении почти стационарного поведения объекта по оптимизируемому фактору возникают новые сложные проблемы:
○ необходимость описания выделенной части поверхности отклика полиномом второго порядка;
○ необходимость варьирования переменных уже, как минимум, на трех уровнях для возможности оценки кривизны этой поверхности;
Последняя проблема приводит к росту числа необходимых опытов до 3к. Для ее решения названными ранее авторами предложена идея построения композиционных планов, предполагающая при попадании в стационарную область постановку опытов с использованием линейных планов. Только убедившись в том, что гипотеза линейности не верна, исследователь достраивает линейный план до плана второго порядка.
Стратегию построения композиционного плана можно продемонстрировать на примере задачи с тремя переменными (рис 5.7):
○ постановка опытов по линейному плану в точках, заданных вершинами правильного симплекса (зачерненные точки);
○ постановка опыта в центре куба для проверки гипотезы адекватности линейной задачи;
○ при нарушении адекватности линейной задачи число опытов увеличивается за счет оставшихся не использованных точек куба (не зачерненные точки);
добавляется к ним еще ряд «звездных точек», образующих октаэдр (точки помечены звездочками).
Получается композиционный план экспериментов второго порядка. Границы варьирования переменных расширяются. В таком плане второго порядка содержится (при к=3) всего лишь 15 точек вместо 27 в полном факторном плане типа 33.
○
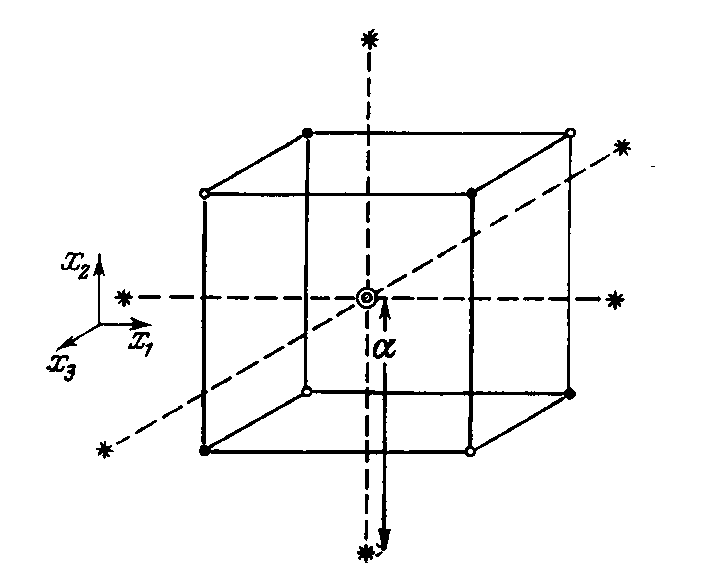
Рис.5.7 Обследуемое пространство существования объекта
при композиционном планировании .
При использовании композиционного плана возникает очень непростая задача, касающаяся выбора расстояния α до звездных точек.
Первое предложение авторов идеи – сохранение ортогональности композиционного плана второго порядка: равенства скалярного произведения всех векторов–столбцов нулю. Однако такие планы оказались не ротатабельными, и дисперсии оценок коэффициентов регрессии у них не минимальны, поэтому Бокс и Хантер предположили использовать при построении таких планов критерий ротатабельности.
Из всех выше приведенных замечаний по ортогональности и ротатабельности планов эксперимента следует сделать вывод о необходимости подбора размещения точек, в которых будут проводиться эксперименты, для обеспечения того или иного свойства при составлении регрессионной зависимости. Конечно, в наши исследования не должны входить теоретические вопросы такого подбора экспериментальных точек (они для многих экспериментальных планов проделаны математиками- специалистами по математической теории эксперимента), но мы должны знать путь, по которому они шли, чтобы со знанием дела применять разработанные ими планы эксперимента.
Опираясь на некоторые начала наших знаний в линейной алгебре матричного исчисления, которые предусматриваются программой по курсу математики высшей школы, рассмотрим алгоритм вычисления оценок коэффициентов регрессионных уравнений и их среднеквадратичных отклонений.
В матричной форме уравнение регрессии может быть записано следующим образом:
Х·В=У, (а)
где Х- матрица условий эксперимента объекта размерности k (где k - число неизвестных коэффициентов в уравнении, В-матрица неизвестных коэффициентов, У- матрица результатов опытов:
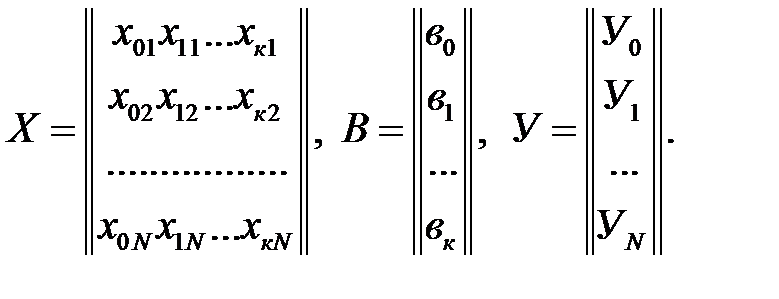
Умножение обеих частей зависимости (а) на транспонированную матрицу условий эксперимента дает:
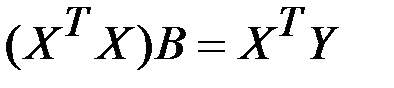 . (в)
. (в)
Произведение матриц 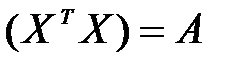 вычисляют следующим образом:
вычисляют следующим образом:
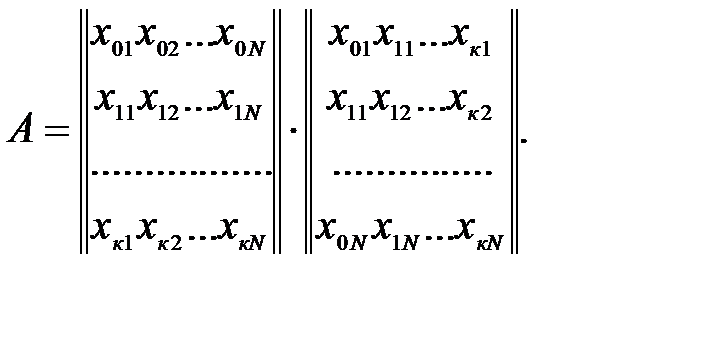
Как известно из матричного исчисления, это произведение даст матрицу той же размерности, что и матрица экспериментов. Матрица А (если она не вырождена) имеет обратную матрица 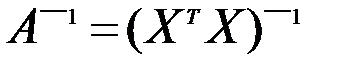 . Если умножить на нее левую и правую части зависимости (в), то получится:
. Если умножить на нее левую и правую части зависимости (в), то получится:
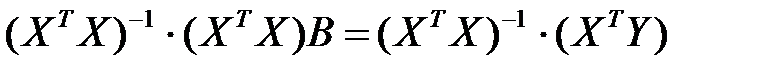 .
.
Произведение обратной матрицы на саму матрицу дает единичную матрицу Е, следовательно, выше приведенная зависимость принимает вид:
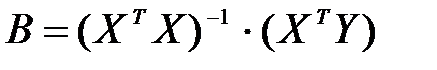 . (5.9)
. (5.9)
Обратная матрица А-1 рассчитывается по формуле:
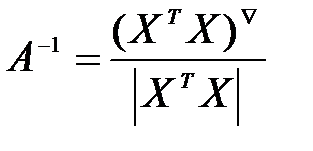 ,
,
где 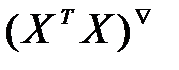 - присоединенная матрица, то есть матрица, в которой элементы замещены их алгебраическими дополнениями, а затем произведено транспонирование;
- присоединенная матрица, то есть матрица, в которой элементы замещены их алгебраическими дополнениями, а затем произведено транспонирование; 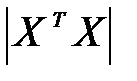 - определитель матрицы
- определитель матрицы 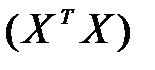 .
.
Расчет матрицы А-1 при большой размерности - трудоемкая задача, но все это можно проделать на ЭВМ (например, в МАТНСАD) в автоматическом режиме. В общем случае матрица А-1 будет иметь следующий вид:
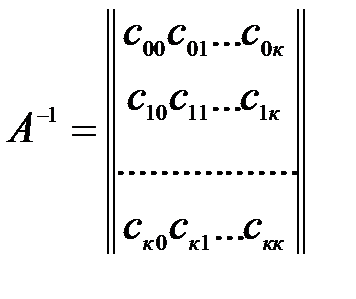 . (5.10)
. (5.10)
Матрица 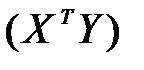 вычисляется по выражению:
вычисляется по выражению:
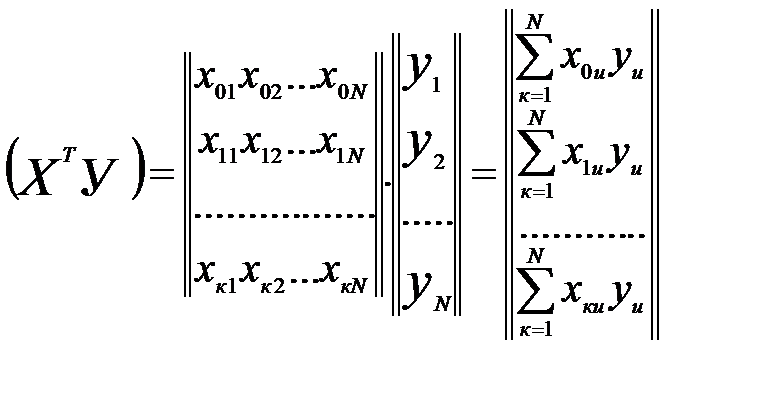 .
.
Теперь решение системы исходного уравнения (а) относительно В будет:
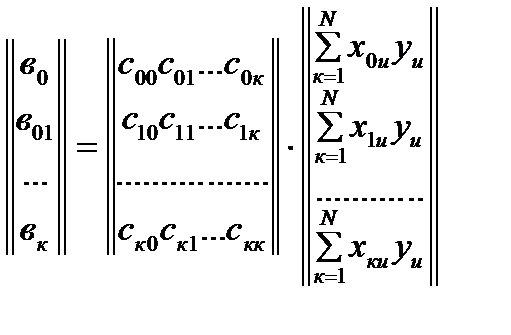 , (5.11)
, (5.11)
или
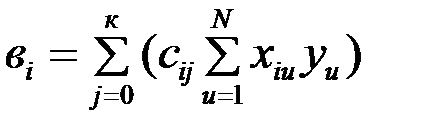 .
.
Точно так дело обстоит с алгоритмом вычисления дисперсии оценки коэффициентов регрессионного уравнения:
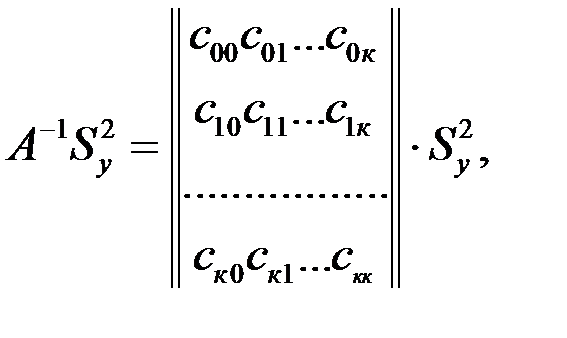 (5.12)
(5.12)
где 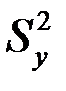 - дисперсия измерения зависимой переменной в экспериментах.
- дисперсия измерения зависимой переменной в экспериментах.
В общем случае это произведение даст следующую матрицу:
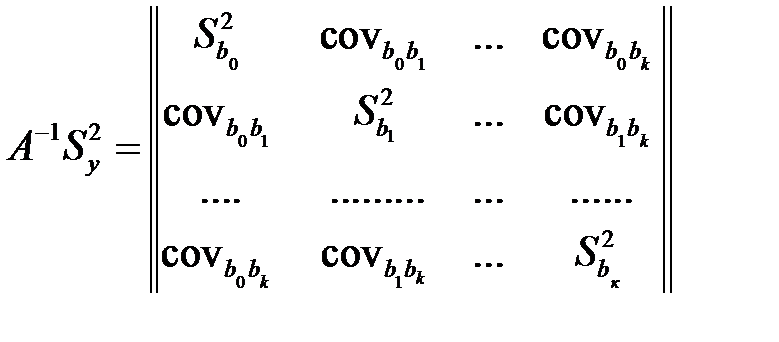 .
.
Откуда и делается заключение о величине дисперсий коэффициентов уравнения регрессии и коэффициентов корреляции между ними:
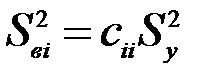 , (5.13)
, (5.13)
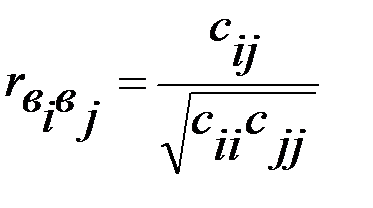 , (5.14)
, (5.14)
где сii, сjj, cij, -соответствующие коэффициенты матрицы А-1.
В общем случае дисперсии коэффициентов по этим зависимостям получаются разными, разными являются и величины взаимной корреляции. В частных случаях из этих выражений получаются те же зависимости, что приводились нами при планировании полных факторных экспериментов при использовании линейных регрессионных зависимостей. При ортогональном планировании все элементы обратной матрицы А-1 сij=0. Сама матрица дисперсий–ковариаций выглядит следующим образом:
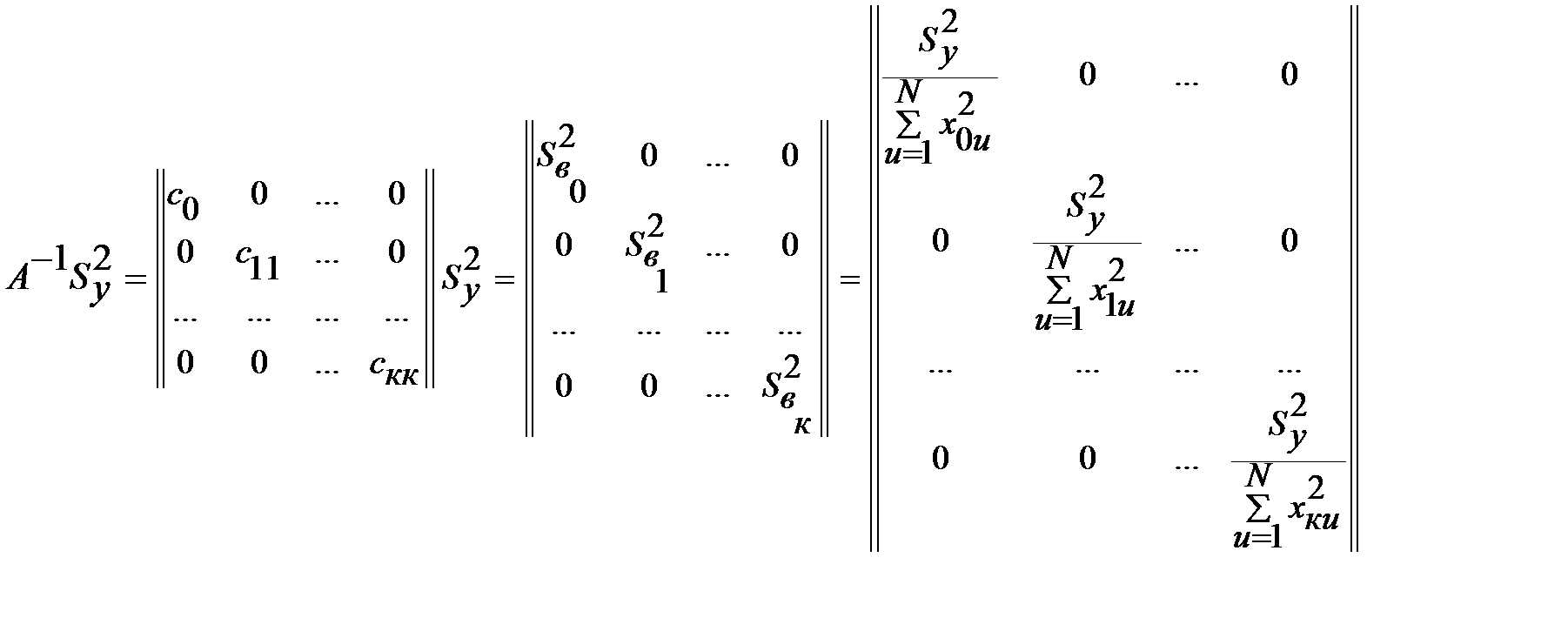 (5.15)
(5.15)
Таким образом, при ортогональном планировании дисперсии оценок коэффициентов регрессии получаются по формуле:
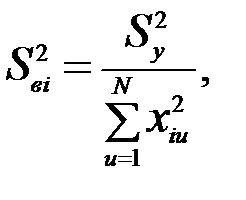 (5.16)
(5.16)
а при условии нормированности плана эксперимента:
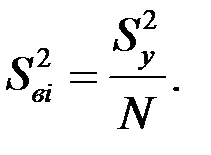 (5.17)
(5.17)
Все ковариации, следовательно, и коэффициенты корреляции между оценками коэффициентов уравнения регрессии равны нулю, что подтверждает независимость рассчитываемых коэффициентов друг от друга.
Расчетные значения выходных переменных, полученные в каких-либо точках пространства существования регрессионной модели, являются случайными, поскольку определенные коэффициенты вi –случайные величины:
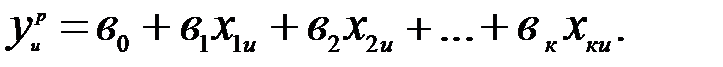 (с)
(с)
Дисперсия этих расчетных значений 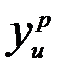 на основании теории ошибок должна иметь величину:
на основании теории ошибок должна иметь величину:
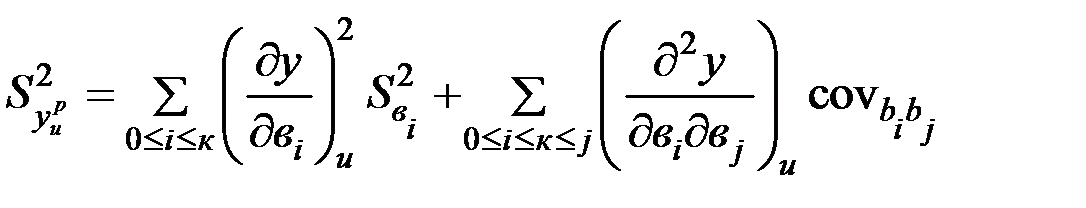 .
.
Поскольку для модели (с) 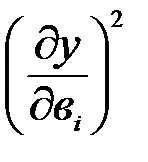 =х2iu, а для ортогональных планов
=х2iu, а для ортогональных планов 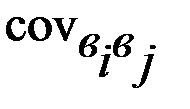 =0 и
=0 и 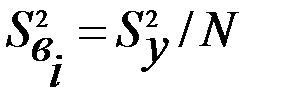 , то можно записать
, то можно записать
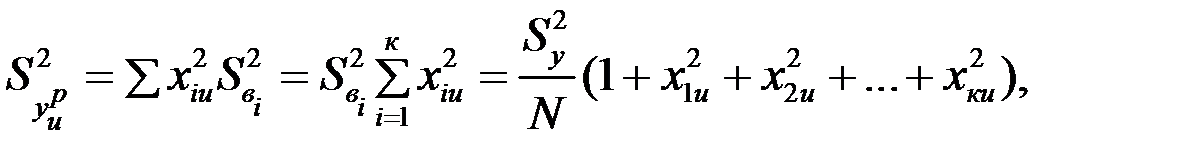
или 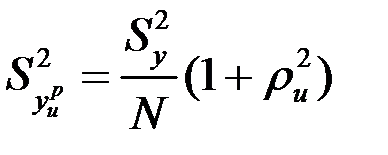 , где
, где 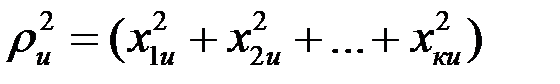 - радиус пространства при равенстве всех значений переменных на основном уровне (хi=0), в котором производится описание результатов эксперимента регрессионным уравнением. В общем случае экспериментальные планы не ортогональны и не ротатабельны.
- радиус пространства при равенстве всех значений переменных на основном уровне (хi=0), в котором производится описание результатов эксперимента регрессионным уравнением. В общем случае экспериментальные планы не ортогональны и не ротатабельны.
Идея использования ротатабельных планов оказалась тоже не безупречной: появилось множество ротатабельных планов (при одном и том же k), для сравнения которых не оказалось критерия.
Как ортогональные, так и ротатабельные планы, задаваемые рисунком 5.7, оказались совсем не удачными. В этом случае при переходе от линейных планов к планам второго порядка принцип оптимального использования пространства независимых переменных оказался нарушенным. Границы варьирования независимых переменных задаются уже не кубом, координаты которого образуются не перестановкой чисел (±1,±1,±1), а перестановкой чисел (±α, ±α, ±α), не все пространство независимых переменных, отведенное для экспериментов, используется в композиционных планах.
Теоретический анализ возникших проблем (Кифер, США) выдвинул несколько критериев для оценки композиционных планов (здесь они не рассматриваются). Если в теории оценок Фишера эффективность оценок задается только оптимальным способом обработки результатов наблюдений, то в концепции Кифера эффективность обусловливается еще и оптимальным расположением точек в пространстве независимых переменных. На основании этого множество решений, построенных на интуитивном уровне, удалось рассмотреть с единых теоретических позиций.
Последние заметки показывают, насколько сложен и извилист путь математического планирования эксперимента (подчеркнем еще раз как натурного, так и вычислительного).
5.4.1 Статистическая обработка результатов эксперимента.
Проведению эксперимента, как уже отмечалось ранее, предшествуют обоснование и выбор плана эксперимента.
Для исключения влияния не учитываемых факторов (для разных исследовательских работ они разные) эксперименты по выбранному плану должны проводиться рандомизированно, т.е. в случайной последовательности. Порядок проведения опытов можно выбирать по таблице случайных чисел. Последнее замечание относится к натурным экспериментам. Вычислительный эксперимент своим алгоритмом исключает влияние на результат неучтенных переменных.
При организации натурного эксперимента предварительно необходимо оценить дисперсию опыта Sy2. Она может быть получена и до начала эксперимента (по ранее проведенным опытам), обычно ее оценивают при подготовке или при проведении опытов. Для повышения ее точности используется дублирование (увеличение повторности) опытов.
Необходимо при этом помнить, что оценка среднего квадратичного отклонения содержит в себе не только оценку неточности производимых измерений, но и оценку динамичности изучаемого процесса (например, нагружения любого сооружения, машины). Названная последняя составляющая сама является характеристикой состояния объекта, определение (выделение) которой является обязательным условием исследования.
В общем случае используется дублирование всех опытов с одинаковой повторностью. В сельскохозяйственных исследованиях, проводимых в полевых условиях на реальных объектах, дублирование всех объектов сложно, дорого, поэтому в них рекомендуется оценивать Sy2 по многолетним статистическим данным или проведением опытов с дублированием в центре экспериментального плана. Тогда 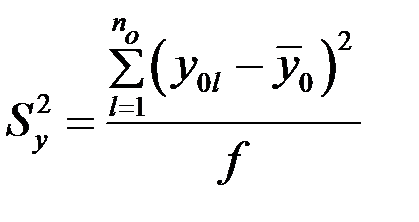 , где no – повторность опытов в центре плана, yol – результат ℓ-го дубля,
, где no – повторность опытов в центре плана, yol – результат ℓ-го дубля, 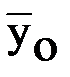 – среднее арифметическое значение всех no дублей, f – число степеней свободы.
– среднее арифметическое значение всех no дублей, f – число степеней свободы.
В рассматриваемом случае по всей совокупности получаемых данных определяется всего одна характеристика, 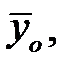 поэтому число степеней свободы оказывается равным f1=n0-1.
поэтому число степеней свободы оказывается равным f1=n0-1.
Затем по ранее приведенным формулам или алгоритмам производится расчет коэффициентов регрессии.
Коэффициенты регрессии должны быть проверены на статистическую значимость. Проверка статистических гипотез предусматривает сравнение выбранного критерия, рассчитанного по экспериментальным данным, с табличным значением при заранее выбранном коэффициенте значимости α и доверительной вероятности (1 - α) - в долях единицы.
Уровень значимости α определяет наибольшую вероятность возможности получения ошибочного результата при вычислении коэффициента регрессии. При α=0,05 вероятность получения правильного результата счета составит 0,95. В случае, если рассчитанный критерий не совпадает при выбранной значимости с табличным, то выбранную гипотезу следует отбросить. Выбранной гипотезой в нашем случае считается зависимость выходного параметра от переменной, коэффициент регрессии которой мы исследуем на статистическую значимость.
Для проверки значимости коэффициентов регрессий вычисляются оценки их дисперсий по приведенным в этом разделе формулам, эти оценки затем используются для сравнения величин самих коэффициентов регрессии с доверительными интервалами, в которые они попадают при заданной статистической значимости при располагаемом количестве степеней свободы f1. В этом случае используется t – критерий Стьюдента. Расчетные значения t – критерия получается по формуле :
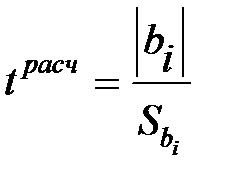 . (5.18)
. (5.18)
Коэффициент значим, если 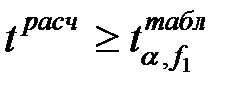 , где
, где 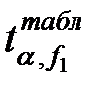 выбирается по таблице критерия Стьюдента при значимости его α и при числе степеней свободы f1 (таблица 5.1).
выбирается по таблице критерия Стьюдента при значимости его α и при числе степеней свободы f1 (таблица 5.1).
Статистическая незначимость проверяемого коэффициента (нарушение приведенного неравенства) означает независимость состояния объекта (по зависимой переменной) от соответствующей переменой.
При ортогональных планах незначимые коэффициенты из модели могут быть исключены без пересчета остальных коэффициентов.
При использовании коэффициентов экспериментальных планов, не обладающих свойствами ортогональности, следует оценивать совместную доверительную область одновременно для всех коэффициентов (эллипсоид рассеивания оценок коэффициентов регрессии). Проверка статистической значимости при этом становится сложной задачей. Многие специалисты по математическому планированию экспериментов рекомендуют в этом случае проверять гипотезу значимости коэффициентов регрессии по t – критерию. При их статистической незначимости по t- критерию отбрасывать незначимые по нему коэффициенты не рекомендуется. Отбрасывание таких коэффициентов возможно только проведением последовательного регрессионного анализа.
| Критические значения t-критерия Таблица 5.1 | |||||||
| Число степеней свободы t | Уровни значимости α | Число степеней свободы f | Уровни значимости α | ||||
| 0,1 | 0,05 | 0,01 | 0,1 | 0,05 | 0,01 | ||
| 6,31 2,92 2,35 2,13 2,02 1,94 1,90 1,86 1,83 1,81 1,80 1,78 1,77 1,76 1,75 | 12,7 4,30 3,18 2,78 2,57 2,45 2,37 2,31 2,26 2,23 2,20 2,18 2,16 2,15 2,13 | 63,66 9,93 5,84 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,06 3,01 2,98 2,95 | ∞ | 1,75 1,74 1,73 1,73 1,73 1,72 1,72 1,71 1,71 1,71 1,71 1,70 1,70 1,70 1,70 1,64 | 2,12 2,11 2,10 2,09 2,08 2,08 2,07 2,07 2,06 2,06 2,06 2,05 2,05 2,05 2,04 1,96 | 2,92 2,90 2,88 2,86 2,85 2,83 2,82 2,81 2,80 2,79 2,78 2,77 2,76 2,76 2,75 2,58 |
Еще раз отметим, что все изложенное выше относится к статистической обработке результатов натурного эксперимента.
При вычислительном эксперименте возникает ряд особенностей. Априорные оценки точности вычисляемых величин по математической модели, как правило, не производятся. Дисперсия их по отношению к действительным процессам оказывается неизвестной, поэтому и рассеивание коэффициентов регрессии не может быть предсказано.
Дисперсия выходных переменных может быть оценена погрешностью принятого метода вычисления. Например, при интегрировании систем дифференциальных уравнений разными методами можно оценить погрешность вычисления величиной, пропорциональной hk, где h – интервал квантования переменных, а k – наименьшая степень отбрасываемых слагаемых в ряде Тейлора. Впрочем, интервал квантования при вычислениях на ЭВМ можно изменять так, что практически вычисленное значение будет отличаться от точного на ошибку округления счета. В таких случаях оценка Sy2 теряет смысл. Проверка сходимости результатов счета и описания его результатов регрессионной моделью должна быть отложена до проведения верификации результатов теоретической оптимизации экспериментальными методами (т.е. до получения послеопытной, апостериорной оценки).
При расчете математических моделей с изменяющимися во времени переменными выходные (зависимые или оптимизируемые) переменные характеризуются не только средними арифметическими значениями, но и их дисперсиями, которые являются оценками динамичности поведения объекта. В таких математических моделях оценка среднего будет зависеть от дисперсии как характеристики динамичности процесса. Оценка значимости коэффициентов регрессионного уравнения в этом случае может быть проведена по критерию Стьюдента, при числе степеней свободы, подсчитываемой по количеству точек разбиения экспериментальных реализаций входных переменных на некотором промежутке времени.
Следующим этапом обработки данных эксперимента является проверка гипотезы об адекватности модели, призванной решить вопрос о приемлемости полученного регрессионного уравнения для описания массива опытных данных или необходимости использования более сложной регрессионной зависимости.
Проверка на адекватность осуществляется с помощью критерия Фишера (F -критерия):
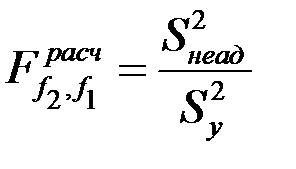 , (5.19)
, (5.19)
где Sy2, как и раньше, дисперсия опытных данных, определенная при числе степеней свободы f1, а Sнеад2 – дисперсия неадекватности, которая определяется по формуле:
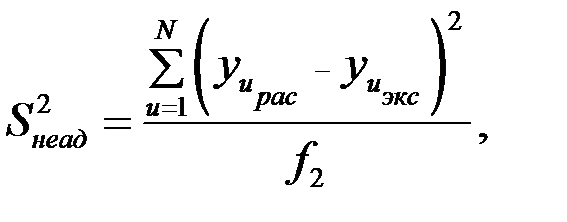 (5.20)
(5.20)
где 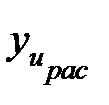 ,
, 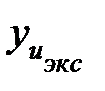 - значения зависимой переменной в u–том опыте, соответственно полученные расчетом по уравнению регрессии и в эксперименте; f2 - число степеней свободы, определяемое как (N-k') при числе опытов плана N и числе оставленных (после проверки значимости) коэффициентов уравнения k' (включая и свободный член).
- значения зависимой переменной в u–том опыте, соответственно полученные расчетом по уравнению регрессии и в эксперименте; f2 - число степеней свободы, определяемое как (N-k') при числе опытов плана N и числе оставленных (после проверки значимости) коэффициентов уравнения k' (включая и свободный член).
Критерий Фишера оценивает точность предсказания состояния объекта по рассматриваемой зависимой переменной по сравнению с опытными данными.
Статистическая модель (регрессионных уравнений) признается адекватной реальному объекту при соблюдении следующего неравенства:
Fрасх≤Fтабл . (5.21)
Табличные значения критерия Фишера приведены в таблице 5.2.
Следует помнить, что формула для подсчета S2неад – справедлива лишь при условии отсутствия дублирования опытов в матрице планирования и использовании дисперсии опыта Sy2, полученной по опытам, не входящим в план. В других случаях используется скорректированные формулы.
Другой способ определения адекватности регрессионной математической модели, построенной по результатам полного или дробного факторного эксперимента типа 2к или 2к-р, опирается на оценку свободного члена уравнения b0, являющуюся оценкой не только истинного свободного члена, но и неучтенного влияния вторых степеней независимых переменных:
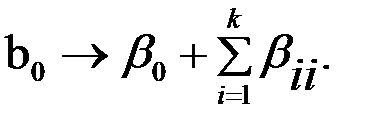
С другой стороны b0 является оценкой опыта в центре плана, когда уровни всех факторов в кодовом масштабе равны нулю. Поэтому разность │b0-y0│, где y0 –экспериментальное значение функции, подлежащей оптимизации, в центре плана экспериментов, является оценкой суммы квадратичных членов в уравнении регрессии. Если эта разность │b0-y0│ -велика (вернее, значима), то гипотеза о нелинейности неприемлема, и потому надо перейти к регрессионному уравнению второго порядка. Значимость этой разности проверяется и в этом случае также по критерию Стьюдента:
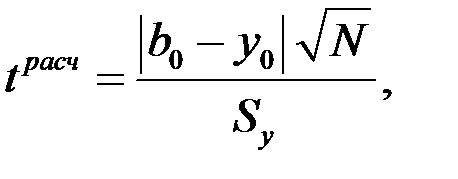 (5.22)
(5.22)
где Sy – среднеквадратичная ошибка опыта, определенная при числе степеней свободы f1.
Гипотеза адекватности уравнения не отвергается, если
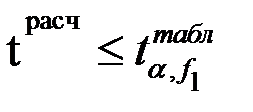 .
.
Сказанное выше без оговорок относится к обработке результатов натурных опытов.
В случае построения регрессионной модели по результатам вычислительного эксперимента представленным выше методом должна проверяться ее адекватность расчетным данным, полученным на ЭВМ. Если мы не оценивали априорную погрешность расчетных данных, то проверку адекватности модели приходится отложить до ее экспериментальной верификации оптимальных показателей.
При исследовании математических моделей с изменяющимися во времени переменными по регрессионным моделям оценка адекватности принятого регрессионного уравнения производится так же, как при аппроксимации экспериментальных данных.
5.4.2 Анализ результатов эксперимента по регрессионным уравнениям второго порядка
Как уже говорилось ранее, для описания экспериментальных данных
в многофакторных системах второго порядка для выявления кривизны поверхности отклика необходимо использовать не двухуровневые планы, а планы с количеством уровней не менее 3, т.е. планы типа, по крайней мере, 3к. Некомпозиционные планы обладают многими положительными свойствами.
Среди них наиболее разработанными являются D-оптимальные по Киферу планы, основанные на теории совместных эффектов.
Основным преимуществом D-оптимальных планов является минимизация обобщенной дисперсии или эллипсоида рассеивания оценок параметров. Эффективность D-оптимальных планов обусловливается оптимальным расположением точек в пространстве факторов. Отличительной особенностью их является наличие во всех строках планов некоторых факторов на нулевом уровне.
В качестве примера некомпозиционного плана типа 3к, часто используемого в работах сельскохозяйственного профиля, приведем здесь некоторые характеристики плана Рехтшафнера. От других некомпозиционных планов (Бокса-Бенкина, Хартли) он отличается более высокой D- оптимальностью и минимальным числом опытов.
В планах Рехтшафнера используются четыре множества набора опытов. Все они и их зависимости от размерности исследуемого объекта приведены в таблице 5.3.
Способ построения насыщенных планов Рехтшафнера.
Таблица.5.3
| Номер множества | Точки множества | Число опытов множества |
| I | (-1,…,-1) для всех k | |
| II | (-1,1,…,1) для всех k | k |
| III | (-1,-1,1) для k=3 (1,1,-1,…,-1) для k>3 | 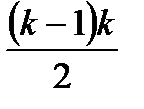
|
| IV | (1,0,…,0) для всех k | k |
Пример использования указанных множеств при построении плана Рехтшафнера для исследования объекта размерностью к=5 приведен в таблице 5.4.
Расчет коэффициентов математической регрессионной модели по плану Рехтшафнера производится по общей методике, приведенной на стр. 127…131.
В общем виде адекватное квадратичное регрессионное уравнение, описывающее результаты эксперимента, имеет вид:
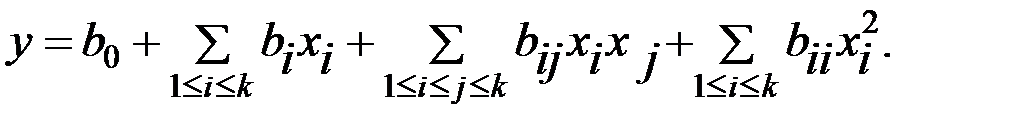
План Рехтшафнера для k=5 Таблица 5.4
| Номер опыта | Х1 | Х2 | Х3 | Х4 | Х5 | Примечания |
| - | - | - | - | - | Множество I из табл. 5.3 | |
| - | + | + | + | + | Множество II из табл. 5.3 | |
| + | - | + | + | + | ||
| + | + | - | + | + | ||
| + | + | + | - | + | ||
| + | + | + | + | - | ||
| + | + | - | - | - | Множество III из табл. 5.3 | |
| + | - | + | - | - | ||
| + | - | - | + | - | ||
| + | - | - | - | + | ||
| - | + | + | - | - | ||
| - | + | - | + | - | ||
| - | + | - | - | + | ||
| - | - | + | + | - | ||
| - | - | + | - | + | ||
| - | - | - | + | + | ||
| + | Множество IV из табл. 5.3 | |||||
| + | ||||||
| + | ||||||
| + | ||||||
| + |
Часть членов, признанных статистически незначимыми (только на основании последовательного регрессионного анализа), в нем может отсутствовать.
Составление этой модели не самоцель исследования. Оно средство, с помощью которого обычно решается экстремальная задача – отыскание значения переменных, обеспечивающих наилучшее или приемлемое состояние изучаемого объекта.
Анализировать уравнение второй степени можно в том виде, в котором оно представлено выше, но очень сложно. Известны разные алгоритмы отыскания оптимумов регрессионных уравнений, упрощающих путь к достижению цели.
Наиболее распространенным способом такого исследования является алгоритм распознавания формы поверхности, представляемой регрессионным уравнением. В этом случае уравнение приводится к каноническому (стандартному) виду.
Каноническое преобразование связано с выбором системы координат, обеспечивающей геометрическое распознавание поверхности. При таком преобразовании определяется центр поверхности второго порядка (если он есть), в него переносится начало координат (при этом в уравнении исчезают линейные члены 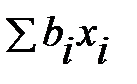 ), которые поворачиваются относительного определенного центра так, чтобы в уравнении исчезли члены
), которые поворачиваются относительного определенного центра так, чтобы в уравнении исчезли члены 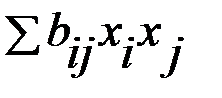 .
.
Регрессионное уравнение второго порядка в канонической форме приобретает вид:
y-ys=B11χ21+B22χ22+…+Bkkχ2k,
где ys – значение поверхности отклика в новом начале координат (свободный член канонического уравнения), χi – новые оси координат, повернутые в многофакторном пространстве на некоторый угол относительно старых осей xi и линейно связанные с ними; Bii – коэффициенты уравнения в канонической форме (канонические коэффициенты). В это уравнение новые коэффициенты входят только во второй степени, поэтому изменение значений отклика (у) зависит только от знака канонического коэффициента, что создает значительные удобства при анализе поверхности отклика.
Все многомерные поверхности отклика могут быть разбиты на три класса:
1. поверхности, имеющие экстремум, когда все канонические коэффициенты имеют одинаковые знаки и центр фигуры находится вблизи центра эксперимента;
2. поверхности типа минимакса, когда канонические коэффициенты имеют разные знаки и центр фигуры находится вблизи центра эксперимента;
3. поверхности типа возрастающего возвышения или гребня, когда часть канонических коэффициентов близка к нулю и центр фигуры удален от центра эксперимента.
Поверхности первого класса практически выявляют лучший вариант (отклик) поведения исследуемого объекта. Проведение дополнительных опытов вблизи расчетных координат обычно приводят к принятию окончательного решения.
Сложнее обстоит дело при принадлежности исследуемой поверхности к двум другим классам. При этом отыскивается условный экстремум в области, где проводятся эксперименты, либо при некоторой разумной их экстраполяции.
Алгоритм канонического преобразования квадратичной модели составляют следующие шаги:
1. Вычисление координат центра поверхности (x1s,x2s,…,xks) решением системы линейных алгебраических уравнений, получающихся после приравнивания к нулю первых производных зависимой переменной по каждому xi: 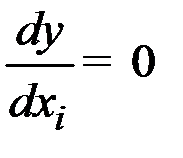 . Если главный определитель, полученный системы не равен нулю, поверхность отклика имеет центр, если равен нулю – не имеет. В последнем случае новый центр помещают в старое начало координат, либо в точку с лучшим значением отклика.
. Если главный определитель, полученный системы не равен нулю, поверхность отклика имеет центр, если равен нулю – не имеет. В последнем случае новый центр помещают в старое начало координат, либо в точку с лучшим значением отклика.
2. Вычисление значения отклика в новом центре (ys), являющегося свободным членом канонического уравнения, подстановкой координат xis в исходное уравнение.
3. Вычисление канонических коэффициентов Bii по характеристи-ческому уравнению системы:
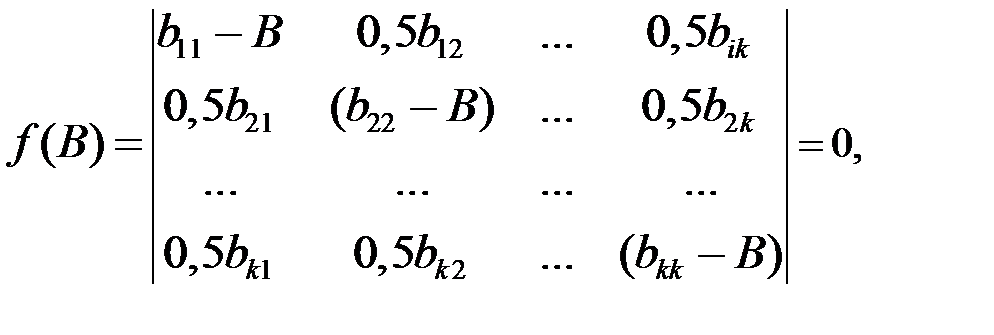
где bij=bji.
Канонические коэффициенты являются корнями этого уравнения. Правильность расчетов подтверждается выражением
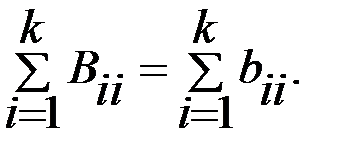
4. Запись регрессионной зависимости в канонической форме и распознавание типа поверхности отклика.
5. Составление систем уравнений для перерасчета старых координат в новые и наоборот:
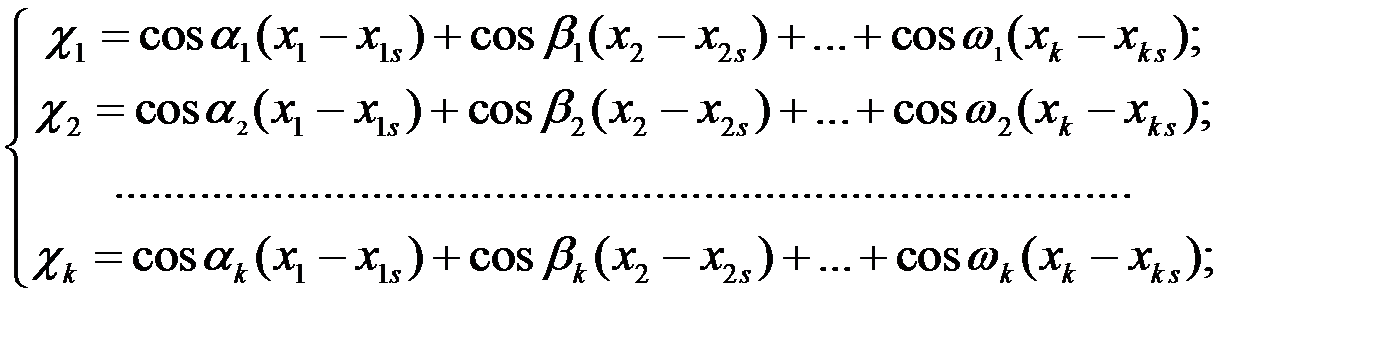
и
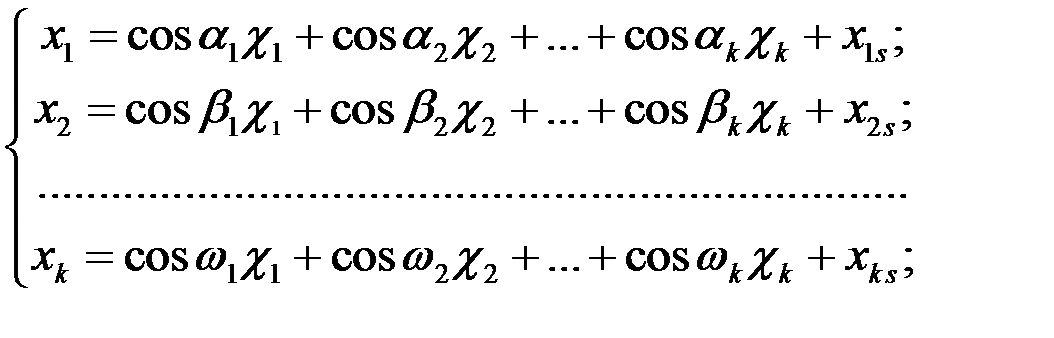
где αi, βi, ωi – углы поворота осей xi до совмещения с осями χi (i=1,2,...,k).
Направляющие косинусы рассчитываются по формулам:
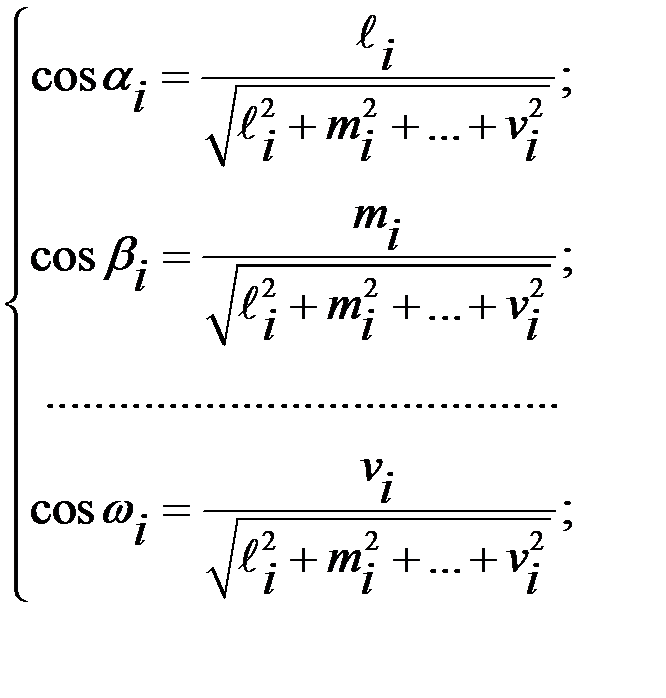
где 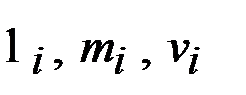 (i=1,2,...,k) вычисляются решением систем уравнений вида:
(i=1,2,...,k) вычисляются решением систем уравнений вида:
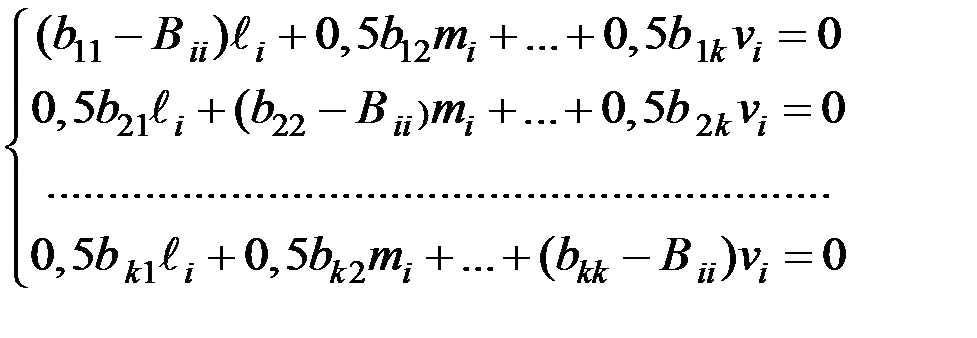
Это система однородных линейных алгебраических уравнений. Если ее главный определитель равен нулю, то все неизвестные системы (ℓi,mi,...vi) равны нулю. Поэтому для решения системы задаются одной из неизвестных произвольно. В этом случае число неизвестных уменьшается на единицу при том же числе уравнений. Такая оставшаяся система решается по матричным уравнениям (5.9) и (5.11).
Правильность вычислений при определении направляющих косинусов можно проверить по формуле :
cos2αi+cos2βi+...+cos2ωi=1.
Изложение алгоритма исследования поверхностей отклика второго порядка, на первый взгляд, должна воодушевить исследователя своей логичностью математической разработки всех вычислительных операций. Это действительно так, если не учитывать проблем на некоторых этапах использования описанного алгоритма. Давайте рассмотрим эти проблемы по порядку:
1. При вычислении канонических коэффициентов по характеристи-ческому уравнению при размерности системы k>4 возникают сложности, связанные с определением его корней. Алгебраические уравнения степеней до четвертой (включительно) решаются стандартно разработанными методами, при степенях выше четвертой отыскание корней усложняется;
2. Формулы для вычисления направляющих косинусов требуют больших вычислительных работ: для этого необходимо решать k (k – размерность системы) групп из k алгебраических линейных уравнений;
3. Отсутствие зрительного образа распознаваемой поверхности, затрудняющего выбор последовательности выполняемых вычислительных операций, ведущих к цели.
Для частичной ликвидации этих проблем часто используется графический способ анализа получаемых статистических моделей.
Обычно строятся двумерные сечения поверхностей отклика, изображающие линии пересечения распознаваемой фигуры плоскостями xi=const. В этом случае в регрессионное уравнение подставляются значения всех переменных кроме любых двух, а затем по двухфакторным зависимостям строятся изолинии равных значений отклика. Уменьшение числа переменных до двух позволяет воспользоваться самым простым вариантом описанного выше алгоритма исследования уравнения. Такой анализ серии сечений наглядно выявляет характер изменения отклика при варьировании факторов и, в конце концов, дает возможность находить компромиссные решения оптимизационной задачи.
Упрощенный алгоритм исследования поверхности состоит в следующем:
1. Вычисление координат центра исследуемой поверхности (xis, xjs):
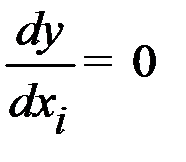 ,
, 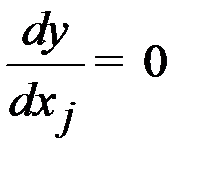 ,
,
где i, j – номера оставляемых переменными факторов;
2. Вычисление отклика (оптимизируемой зависимой переменной) в центре поверхности ys по двухфакторной регрессионной зависимости;
3. Запись уравнения регрессии в двухфакторном виде
y-ys=bijxij+biixi2+bjjxj2,
где xi, xj – оставленные переменными независимые факторы.
4. Вычисление канонических коэффициентов по уравнению:
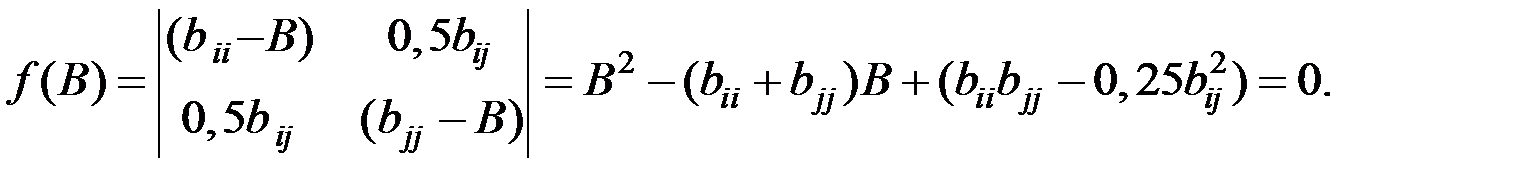
Два корня характеристического уравнения являются каноническими коэффициентами Bii и Bjj;
5. Определение угла поворота осей координат
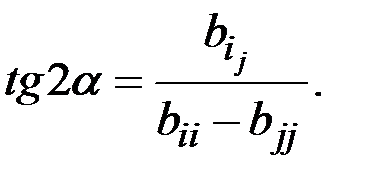
При отрицательном значении α оси поворачиваются по часовой стрелке, положительном – в обратную сторону;
6. Запись факторного канонического уравнения в виде:
y-ys=Biiχi2+Bjjχj2;
7. Построение изолиний (линий равных значений оптимизируемого параметра у) и вычисление оптимальных значений xi и xj.
Дальнейшие шаги связаны с физической природой принятых постоянными факторов. Если новая пара факторов равнозначна первым двум (xi и xj) по степени влияния на формирование оптимума, то с ними поступают так же, как с xi , xj , считая теперь их постоянными при уже определенных оптимальных значениях. После попарного перебора всех переменных можно провести повторный (уточняющий) расчет по всем переменным. На базе полученных частных оптимальных решений может быть выбрано компромиссное заключение по оптимальному варианту.
Дата добавления: 2015-11-12; просмотров: 1857;
