Оптимизация задач при нелинейном программировании
Особенностью задач линейного программирования является наличие ряда качеств, облегчающих отыскание их решения:
1) в задачах линейного программирования существует абсолютный экстремум целевой функции, что устраняет необходимость дополнительных проверок результата решения;
2) множество точек, в которых целевая функция z= 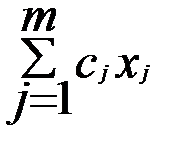 принимает постоянное значение, есть гиперплоскость, определяемая уравнением
принимает постоянное значение, есть гиперплоскость, определяемая уравнением 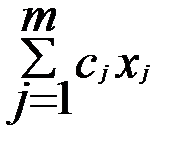 =const, причём, гиперплоскости, отвечающие разным значениям константы, параллельны между собой, что исключает трудности решения, связанные с пересечением поверхностей уровня;
=const, причём, гиперплоскости, отвечающие разным значениям константы, параллельны между собой, что исключает трудности решения, связанные с пересечением поверхностей уровня;
3) область определения линейной задачи является выпуклой и имеет конечное число вершин (крайних точек), и экстремум обязательно достигается в одной из них, которой при решении можно достичь за конечное число шагов, положенное в основу счета по симплекс- методу.
Отсутствие названных особенностей и приводит к трудностям решения задач нелинейного программирования. В каждой из таких задач могут появиться свои разные особенности, мешающие поиску решения задач оптимизации.
В общем случае признаком экстремума считается равенство нулю частных производных:
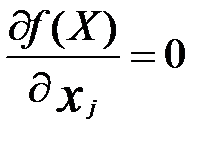 (при j=1,2,3,…n).
(при j=1,2,3,…n).
Это равенство действительно необходимо, но недостаточно. Оно выполняется и в точках перегиба, насыщения и в седловых точках:
| f(x) |
| f(x) |
| f(x1,x2) f(x) f(x) |
| x |
| x |
| x1 |
| x2 |
| Точка перегиба |
| Точка насыщения |
| Седловая точка |
| Рис. 5.1 |
Наиболее простыми при этом являются задачи безусловной оптимизации (без ограничения). При этом используется следующий алгоритм:
1) отыскание всех стационарных точек путём решения уравнений вида 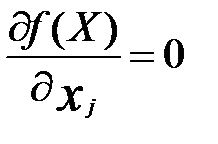 (при j=1,2,3,…n);
(при j=1,2,3,…n);
2) вычисление в каждой определённой точке значений f(x);
3) отыскание среди полученного массива вычислений максимального или минимального, а потом и координат точек, в которых они наблюдаются.
Введение каких-либо ограничений (даже самых простых) усложняет дело. Процедура отыскания координат глобального экстремума (максимум - максиморум, минимум-миниморум) включает и исследование поведения функции на границах области определения функции f(x).
Алгоритм этого исследования даже при таком простом ограничении, как неотрицательность переменных, удлиняется и усложняется. Он включает отыскание: 1) всех внутренних стационарных точек; 2) стационарных пограничных точек на границах, на которых все переменные, кроме одной, равной нулю, строго положительны; 3) всех стационарных точек границ, определяемых равенством нулю попарных переменных; 4) стационарные точки границ с равенством нулю по трём переменным и т.д. По полученным расчетным данным, наконец, из них обычным сравнением f(x) во всех определённых стационарных точках определить глобальный искомый экстремум.
Задача становится громоздкой: общее количество уравнений, подлежащих решению, равно 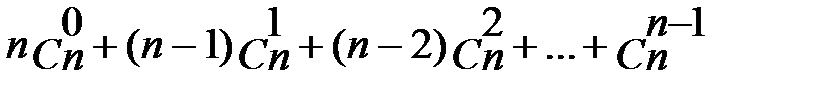 (всего их 2п – 1). Как всегда, в этом случае нужны обходные пути. Частных задач много, но наиболее известным способом решения является метод множителей Лагранжа. Этот метод применяется прежде всего к классическим задачам с ограничениями-равенствами (при отсутствии требований неотрицательности и целочисленности переменных).
(всего их 2п – 1). Как всегда, в этом случае нужны обходные пути. Частных задач много, но наиболее известным способом решения является метод множителей Лагранжа. Этот метод применяется прежде всего к классическим задачам с ограничениями-равенствами (при отсутствии требований неотрицательности и целочисленности переменных).
Порядок составления алгоритма решения рассматривается далее на примере задачи с двумя переменными и с одним ограничением ( т.е. при размерности задачи: п = 2, m = 1). При этом отыскиваются необходимые условия, которым должны удовлетворять координаты точки локального экстремума Х0, если заданы непрерывные и, по крайней мере, дважды дифференцируемые функции f(x1,x2) и g(x1,x2) .
Ограничение g(x1,x2) =b, должно удовлетворять условиям существования неявных функций.
| z |
| x2 |
| x1 |
| Х0 |
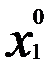
|
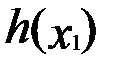
|
| z0 |
| Рис. 5.2 |
Если эти оговоренные условия выполнены, то из условия, что g(x1,x2)=b, можно определить переменную x2 в виде функции x1 и получить
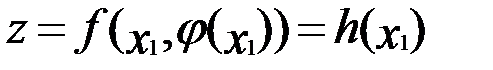 .
.
Ограничение g(x1,x2)=b указывает на то, что нас должны интересовать из всех точек плоскости x1 x2 только те, которые лежат на линии, определяемой уравнением x2= 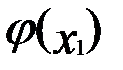 . Если в какой-либо из этих точек (Х0)
. Если в какой-либо из этих точек (Х0) 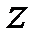 достигает локального экстремума (это условный экстремум), то и функция
достигает локального экстремума (это условный экстремум), то и функция 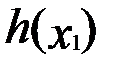 достигает экстремума в точке
достигает экстремума в точке 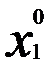 , являющейся координатой х1 точки Х0.
, являющейся координатой х1 точки Х0.
Экстремум 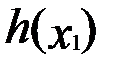 - тоже локальный, но он не является условным, потому что сам способ построения функции
- тоже локальный, но он не является условным, потому что сам способ построения функции 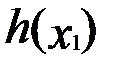 предусматривал учёт исходного ограничения. В других дополнительных требованиях к x1 уже нет надобности. Значит, величина координаты в точке
предусматривал учёт исходного ограничения. В других дополнительных требованиях к x1 уже нет надобности. Значит, величина координаты в точке 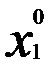 может быть найдена из уравнения
может быть найдена из уравнения
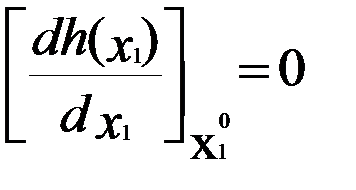 .
.
Так как 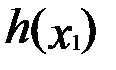 =
= 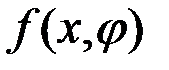 , можно на основании предыдущего условия написать:
, можно на основании предыдущего условия написать: 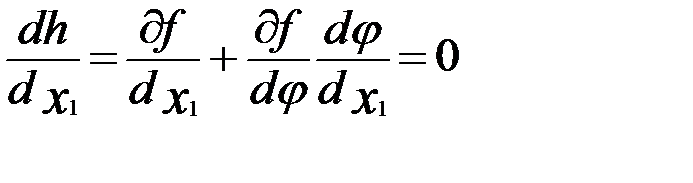 .
.
Учитывая, что 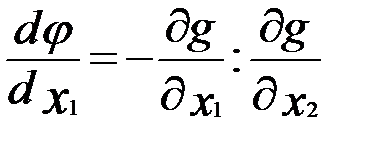 , можно преобразовать последнее равенство:
, можно преобразовать последнее равенство:
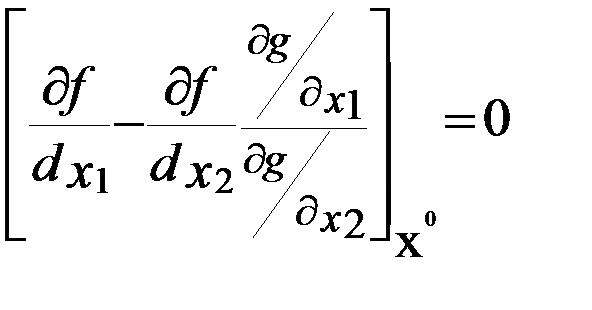 . (5.1)
. (5.1)
Если при 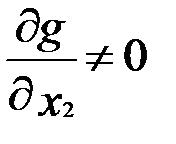 обозначить отношение
обозначить отношение 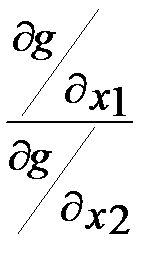 через λ, получим
через λ, получим
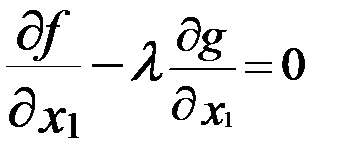
 ,
,
а из определения λ через Х0и его экстремум справедливо будет и
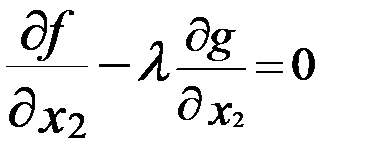 .
.
И теперь условия существования локального экстремума в точке Х0 предстанет в виде трёх уравнений:
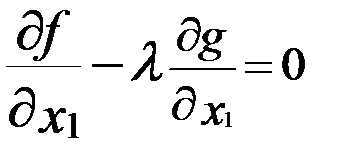 ;
; 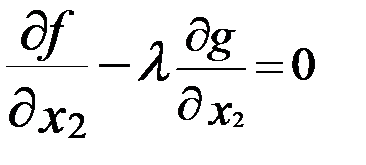 ;
; 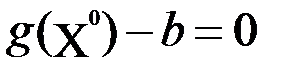 . (5.2)
. (5.2)
Решение системы (5.2) относительно х1, х2 отыскивает все точки типа Х0. Главное удобство этих уравнений в том, что они могут быть получены формальным путём из выражения вида:
f(x1,x2)+λ[b- g(x1,x2)]=Ф(х1, х2, λ).
При независимости друг от друга х1, х2, λ находятся все частные производные 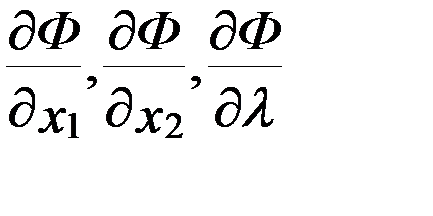 и приравниваются к нулю. Функция Ф(х1, х2, λ) называется функцией Лагранжа, множитель λ – множителем Лагранжа.
и приравниваются к нулю. Функция Ф(х1, х2, λ) называется функцией Лагранжа, множитель λ – множителем Лагранжа.
Математиками произведено обобщение метода множителей Лагранжа на случай произвольного числа переменных n и ограничений m ( m < n ). В этом случае функция Лагранжа принимает вид:
Ф(X,Λ) = f(X)+ 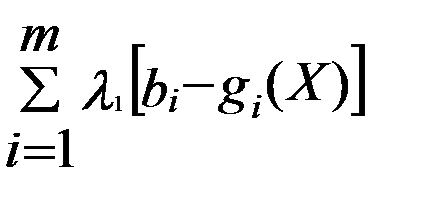 ,
,
где символы X и Λ обозначают совокупность переменных xj (j=1,2,3,…n) и множителей λi (i=1,2,3,…m).
Необходимые условия локального экстремума f(X) получены дифференцированием Ф(X,Λ) по полному набору аргументов и приравниванием каждой полученной производной к нулю:
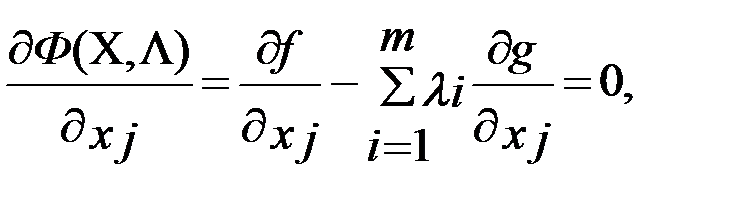
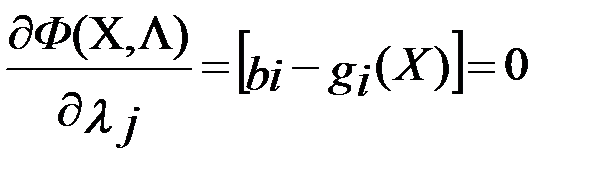 (5.3)
(5.3)
Значит, для отыскания точек Х0 в этом случае приходиться решать систему (m+n) уравнений по типу уравнений системы (5.3). Не обязательно, что любое допустимое решение системы (5.3) будет точкой относительного условного экстремума функции f(X)., но каждая точка, в которой он достигается, удовлетворяет уравнениями (5.3).
Преимущество метода – не надо учитывать взаимную зависимость переменных, недостаток – необходимость решения системы (5.3), задачи не из лёгких.
Математиками доказано обобщение метода множителей Лагранжа на случай нестандартного задания задачи при 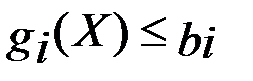 , а также при xj>0. Каждый множитель
, а также при xj>0. Каждый множитель 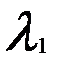 (i=1,2,3,…n),, полученный решением системы (5.3), определяет «реакцию» целевой функции z на изменение соответствующего ему параметра
(i=1,2,3,…n),, полученный решением системы (5.3), определяет «реакцию» целевой функции z на изменение соответствующего ему параметра 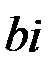 . По величине этого множителя можно судить о том, какое из ограничений при изменении даёт максимальное приращение значения целевой функции.
. По величине этого множителя можно судить о том, какое из ограничений при изменении даёт максимальное приращение значения целевой функции.
Выше названные обобщения метода множителей Лагранжа вряд ли можно считать удобными, потому что они повторяют классический путь исследования на границах области, с решением больших промежуточных задач. Алгоритм такого решения приводится в книге «Основы кибернетики» под редакцией Пупкова.
Естественно искать более удобный способ решения. Таковым является способ, основанный на изучении особенностей функции Лагранжа, которую она имеет в точке глобального экстремума f(X).
Оказалось, что функция Лагранжа в точке глобального экстремума f(X) имеет седловую точку в классическом её виде. Значит, это условие и является необходимым и достаточным для наличия экстремума (глобального условного экстремума) – вот результат доказательства теоремы Куна–Таккера.
Условия существования седловой точки функции Лагранжа, доказанные математиками, записываются следующим образом:
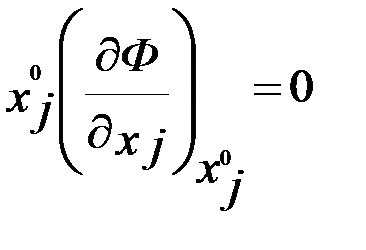 ( j=1,…n);
( j=1,…n); 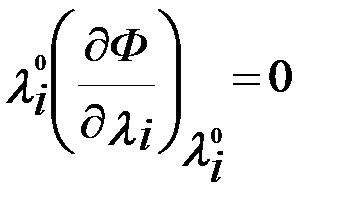 (i=1,…m) . (5.4)
(i=1,…m) . (5.4)
Значит, либо производные 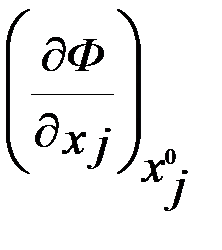 и
и 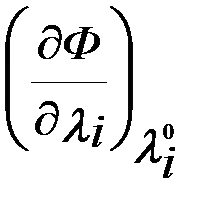 , либо сами переменные
, либо сами переменные 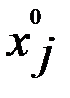 ,
, 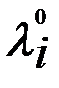 обращаются в нули в седловой точке ( X0,Λ0 ).
обращаются в нули в седловой точке ( X0,Λ0 ).
Достаточность сформулированных условий определяется требованием нахождения просто экстремума f(X) (неизвестно, максимума или минимума). В случае необходимости выявления типа экстремума требуется уточнение условий достаточности.
Исходя из условий, что найденный экстремум будет максимумом функции оптимизации, функция Лагранжа Ф(X,Λ), должна быть вогнутой функцией Х. Выполнение этого требования зависит от соответствующих свойств функций f(X) и g(X) при i=1…m:для достижения f(X) в седловой точке функции Лагранжа глобального условного максимума, необходимо и достаточно, чтобы ее координаты x٭и λ٭ удовлетворяли нижеследующим соотношениям (5.5);
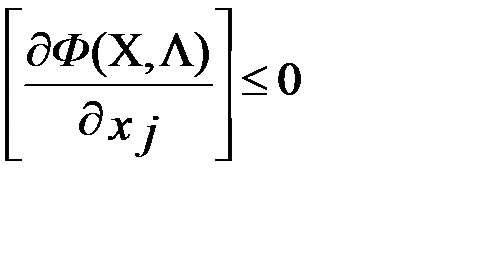 при
при 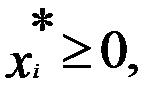
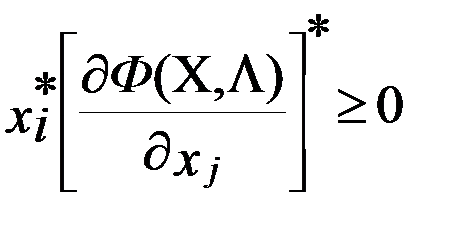 при
при 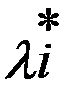 (i=1,2,3,…n),
(i=1,2,3,…n),
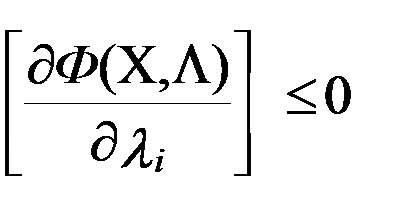 при
при 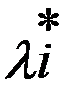 (i= u+1,…, v),
(i= u+1,…, v),
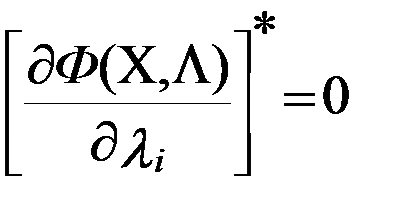 (i= v+1,…,m),
(i= v+1,…,m),
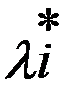
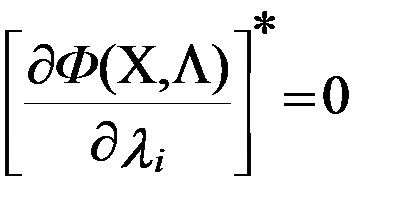 (i=1,2,3,…m).
(i=1,2,3,…m).
В системе условий (5.5):
· n-полное число компонентов вектора переменных X ;
· S - число компонентов вектора X, для которых 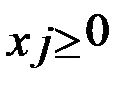 ;
;
· (t-S) - число компонентов того же вектора, у которых 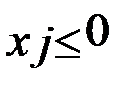 , (S+1,… t);
, (S+1,… t);
· (n- t) - число компонентов вектора X , не имеющих ограничений на знак (t+1… n);
· m –число множителей Лагранжа (число ограничений 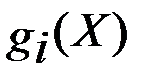 );
);
· u - число положительных множителей Лагранжа и соответственно (v - u) – число отрицательных множителей Лагранжа (u+1,… v), (m – v) - число множителей Лагранжа, не имеющих ограничений на знак (v+1,… m).
Таким образом, для идентификации седловой точки функции Лагранжа максимумом функции f(X) функция должна быть вогнутой при X≥0, а функции 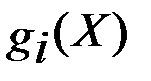 - выпуклыми при
- выпуклыми при 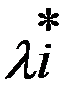 ≥0 и вогнутыми при
≥0 и вогнутыми при  ≤0.
≤0.
В случае, когда отыскивается минимальное значение целевой функции, у неё изменяется знак (умножением на - 1). После этого отыскивается по описанному алгоритму максимум этой новой целевой функции. Полученные этим решением координаты и коэффициенты Лагранжа будут определять местоположение искомого решения (минимума) и его значение, просчитываемое по функции z = f(X).
5.4 Аппроксимация данных вычислительного и натурного экспериментов регрессионными зависимостями.
Невозможность исследования математических моделей в каждой точке пространства их существования приводит к необходимости их оценки с помощью аппроксимационных зависимостей. При этом возникает возможность исследования поведения объекта, описываемого этими математическими моделями, в каждой точке пространства аналитическими методами.
Планы многофакторного анализа в первую очередь используются для оценки линейных эффектов (пропорциональных переменным) и эффектов взаимодействия всех факторов.
Главной особенностью многофакторного анализа является концепция оптимального использования пространства существования объекта математического моделирования.
Пусть в линейной задаче имеется к независимых переменных (x1, x2,...,xk), образующих к-мерное пространство (к ним нужно еще добавить к+1-ую фиктивную переменную – свободный член уравнения регрессии).
Уравнение регрессии в этом случае записывается в виде:
η=β0+β1х1+β2х2+…+βкхк. (5.6)
При этом возникает проблема: отыскание оценок для коэффициентов регрессий βi таких, чтобы они в пределе стремились к самим коэффициентам (bi→βi). Она может быть решена традиционным (однофакторным) методом. Если для каждой переменной делается n повторных опытов с варьированием их только на двух уровнях +1 и -1, то дисперсия оценки коэффициента регрессии окажется σ2(bi)=σ2(y)/2n, и ее величина не будет зависеть от общего числа переменных, т.к. каждая оценка определяется только двумя осредненными измерениями.
Другая стратегия (многофакторного) анализа основывается на одновременном изменении всех переменных, обеспечивающих оценку каждого эффекта по всей совокупности опытов. В благоприятном случае появляется возможность уменьшить дисперсию в (к+1)n раз по сравнению с единичным измерением. Конечно, не все это оказывается просто даже в линейных задачах, не говоря уже о нелинейных, при выборе оптимальных планов эксперимента. Пришлось вводить сложную систему критериев оптимальности планов и развивать совсем непростую математическую теорию, позволяющую в выбираемом смысле оптимально использовать пространство независимых переменных, принятое в исследовании.
Продемонстрируем эту идею очень простым примером – задачей о взвешивании трех объектов A, B и C. При однофакторном исследовании экспериментатор работает по нижеприведенной схеме:
| Номер опыта | А | В | С | Результат взвешивания |
| -1 | -1 | -1 | у0 | |
| +1 | -1 | -1 | у1 | |
| -1 | +1 | -1 | у2 | |
| -1 | -1 | +1 | у3 |
В таблице (+1) свидетельствует о помещении объекта на весы, (-1) – об отсутствии его на весах. Первое взвешивание (по табличной схеме) – холостое, определяющее нулевую точку. Все другие - последовательное взвешивание исследуемых объектов.
Вес каждого объекта оценивается по результатам двух опытов: взвешивания изучаемого объекта и холостого опыта.
А=у1-у0.
Дисперсия результата взвешивания оказывается равной:
σ2(А)=σ2(у1-у0)=2σ2(у),
где σ2(у) – ошибка (среднеквадратичная) взвешивания.
При проведении того же самого эксперимента по новой схеме, представленной следующей таблицей – матрицей, результат взвешивания оказывается более точным:
| Номер опыта | А | В | С | Результат взвешивания |
| -1 | -1 | +1 | у1 | |
| +1 | -1 | -1 | у2 | |
| -1 | +1 | -1 | у3 | |
| +1 | +1 | +1 | у4 |
«Холостое» взвешивание этой матрицей не предусматривается.
Легко видеть, что вес каждого объекта определяется формулами:
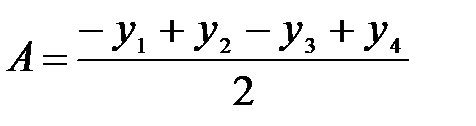 ,
, 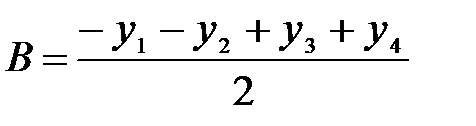 ,
, 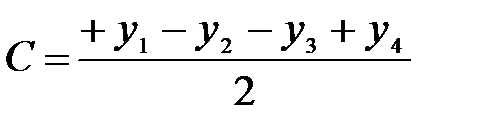 .
.
Числители этих формул получены как произведение последнего столбца матрицы на элементы соответствующих столбцов (А,В,С). При вычислении любого из искомых весов в числитель он входит дважды (в явном порядке и в у4), поэтому в знаменателе появляется двойка. Вес объекта А, например, оказывается не искаженным весами объектов В и С, так как вес каждого из них входит в формулу расчета дважды с разными знаками.
Дисперсия, связанная с ошибкой взвешивания, при новой схеме опытов окажется равной:
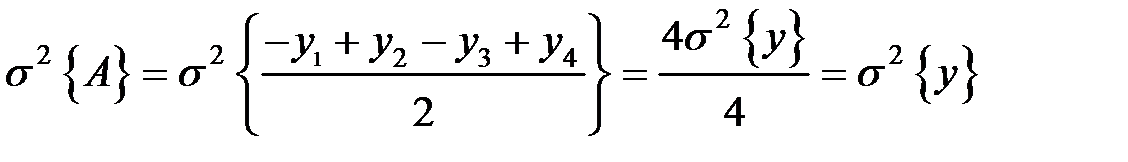 .
.
Точно также σ2{B}=σ2{y} и σ2{С}=σ2{y}, т.е. по новой схеме взвешивания дисперсия получается вдвое меньше, чем при однофакторном исследовании, хотя в обоих случаях было проведено по четыре опыта.
Точность определения весов увеличилась за счет того, что, в отличие первой схемы опытов, во втором случае каждый вес определялся из результатов всех четырех опытов, а не двух (взвешивания объекта и холостого). Вторая схема проведения экспериментов поэтому и называется многофакторным анализом.
Рассмотренный случай очень прост, но по такой схеме могут организовываться и более трудоемкие эксперименты, например, следующие.
Пусть выход некоторого продукта при переработке сельскохозяйственной культуры линейно зависит от трех переменных х1, х2, х3. В частном случае это может быть температура в сушильной камере, давление пресса и время прессования или толщина слоев перерабатываемой культуры. Задача состоит в том, чтобы оценить коэффициенты регрессии линейного уравнения:
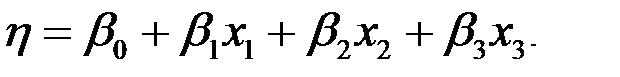
Каждая переменная варьируется на двух уровнях, которые выбираются на основании предварительного исследования их по всем существующим источникам.
Для того, чтобы не писать в ячейки матрицы планирования конкретные значения переменных, производится кодирование переменных. Такое кодирование не только упрощает запись уровней изменения переменных, но и упрощает методику определения коэффициентов регрессионного уравнения и их точности.
Для осуществления операций кодирования:
1. Выбирается исходная область эксперимента заданием верхних и нижних значений пределов изменения каждого фактора в ходе эксперимента Хimax и Хimin. (рис.5.3).
2. Осуществляется центрирование области и перенос начала координат факторного пространства в точку, называемую центром эксперимента с кордитами в х1о,х2о,...,хко (точка О на рис. 5 3), где
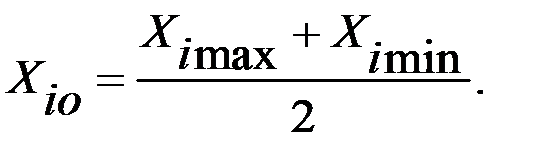 (5.7)
(5.7)
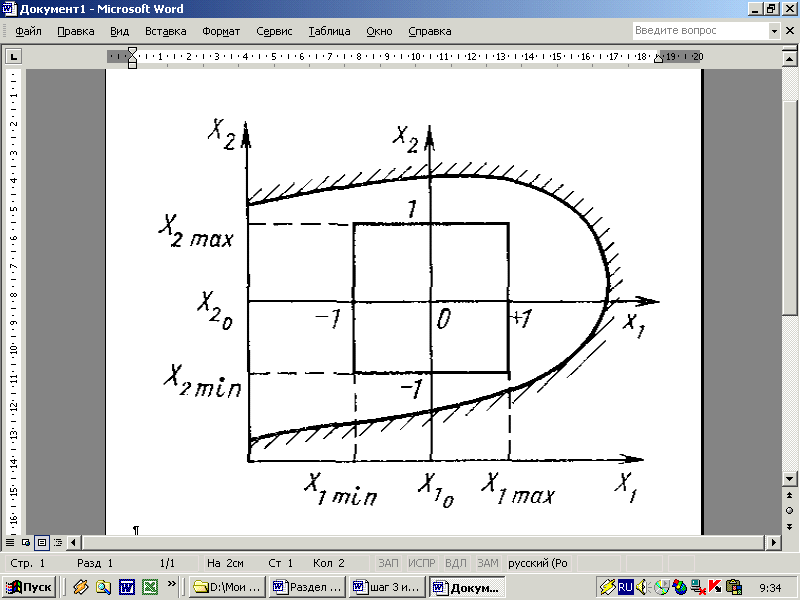
Рис. 5.3 Выделение области эксперимента.
Выбор исходной области - задача непростая. Он осуществляется на основании изучения прежних исследований, если же исследования пионерские, то на основании рассмотрения сущности процессов, протекающих в объекте.
3. Верхние уровни факторов в кодированном масштабе принимаются за +1, нижние - за (-1), а средний - за 0. Пересчет естественных координат в кодированные осуществляется по формулам:
xi= 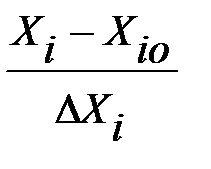 , Xi=Xi0+∆Xixi, если ∆Хi=
, Xi=Xi0+∆Xixi, если ∆Хi= 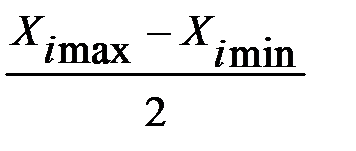 - интервал варьирования.
- интервал варьирования.
В кодированной системе координат факторное пространство ограничено k-мерным кубом (для одного фактора это прямая, для двух- квадрат, для трех - геометрической куб). Теперь величины +1 и -1 означают не присутствие или отсутствие в эксперименте того или иного фактора, а его конкретный уровень в кодированном виде. Еще раз отметим, что при выборе пространства существования объекта и интервалов варьирования необходимо учитывать следующие обстоятельства.
Стремление к получению адекватной модели требует сужения интервалов варьирования (для уменьшения влияния нелинейности). При этом нельзя допускать, чтобы неточности измерения исследуемой функции на суженных интервалах приводили к резкому изменению точности действительного влияния его на рассматриваемый объект (рис 5.4). В общем случае выбор интервалов варьирования зависит от постановки задачи.
Поиск наилучших условий функционирования изучаемого объекта бесполезен, если при постановке задачи не учитывается хотя бы один из факторов со значительным влиянием на объект. Для исключения такой неприятности необходимо проводить их ранжирование (априорно или экспериментально по однофакторным опытам). Такая работа может быть самостоятельным исследованием, осуществляемым по своим структурам математических планов экспериментов (планам дисперсионного анализа или отсеивающих экспериментов).
Для постановки опытов используем матрицу планирования следующего вид:
| Номер опыта | План | Результаты экспериментов | |||
| х0 | х1 | х2 | х3 | ||
| +1 | -1 | -1 | +1 | у1 | |
| +1 | +1 | -1 | -1 | у2 | |
| +1 | -1 | +1 | -1 | у3 | |
| +1 | +1 | +1 | +1 | у4 |
Эта матрица практически не отличается от предыдущей, в ней факторы А, В и С заменены переменными х1, х2, х3 и добавлен столбец фиктивной переменной х0 для оценки свободного члена.
Если приходится иметь дело с семью независимыми переменными, изменяющимися только на двух уровнях, то используется матрица опытов в виде:
| План | Результаты экспериментов | |||||||
| х0 | х1 | х2 | х3 | х4 | х5 | х6 | х7 | |
| +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | у1 |
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | у2 |
| +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | у3 |
| +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | у4 |
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | у5 |
| +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 | у6 |
| +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | у7 |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | у8 |
В этой матрице экспериментов вариантов опытов только на единицу больше независимых переменных. Такие планы называются насыщенными, так как все степени свободы f=N=k+1 используются для оценки k+1 коэффициентов регрессии:
b0→ β0, b1→ β1,..., bk→ βk
Экспериментальные планы, приведенные в предыдущих двух матрицах, обладают следующими свойствами:
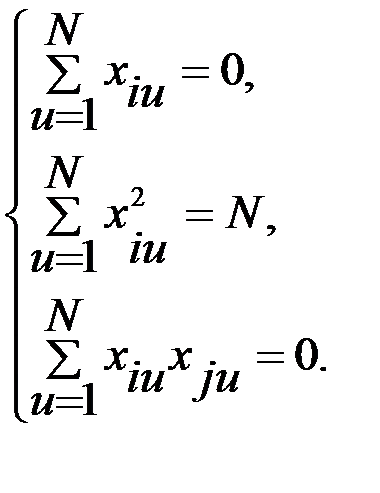 (5,8)
(5,8)
Первое из этих свойств – условие симметричности планов, второе – условие нормирования, третье – ортогональности: скалярное произведение всех векторов–столбцов равны нулю. Последнее свойство определяет независимость вычисления коэффициентов регрессии друг от друга. Второе свойство указывает на то, что все диагональные элементы матрицы произведения (Х*Х) равны 1/N. Система нормальных уравнений распадается на (k+1) независимых уравнений, которые дают:
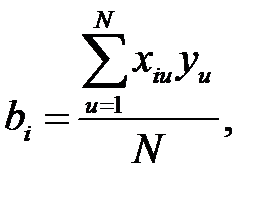
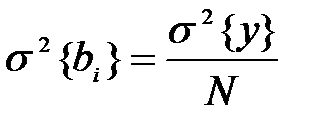 при N=k+1.
при N=k+1.
Оценки коэффициентов регрессии должны быть оптимальными в статистическом смысле: состоятельными, несмещенными, эффективными и достаточными. Состоятельность оценки определяется приближением коэффициента к его истинному значению при увеличении объема выборки экспериментальных данных. Несмещенность оценки означает совпадение ее с математическим ожиданием его рассеивания. Эффективность оценки характеризуется минимальной дисперсией. Достаточность оценки включает максимум информации о коэффициентах.
При использовании последней матрицы к семимерному пространству точность (эффективность) оценки коэффициентов регрессии возрастает в четыре раза по сравнению с матрицей однофакторных экспериментов. Отсюда следует очень важный вывод: с ростом числа независимых переменных (k), включаемых в исследование, эффективность многофакторного эксперимента будет расти как (k+1). Это явление может быть истолковано геометрически. В линейных задачах коэффициенты регрессии определяются тем точнее, чем больше радиус обследуемой сферы пространства существования объекта математического моделирования. В однофакторной задаче это легко иллюстрируется графиком рисунка 5.4.
Черные точки - истинные значения, белые - значения, отсчитанные с ошибками. Отсюда видно, чем дальше разнесены экспериментальные точки, тем точнее оценивается коэффициент регрессии при тех же ошибках измерения.
В реальной исследовательской работе радиус обследуемого пространства произвольно увеличиваться не может. Связано это с двумя причинами:
- границы интервалов варьирования часто жестко задаются условиями существования исследуемого объекта или возможностью техники эксперимента;
- нарушается линейная аппроксимация при расширении области исследования
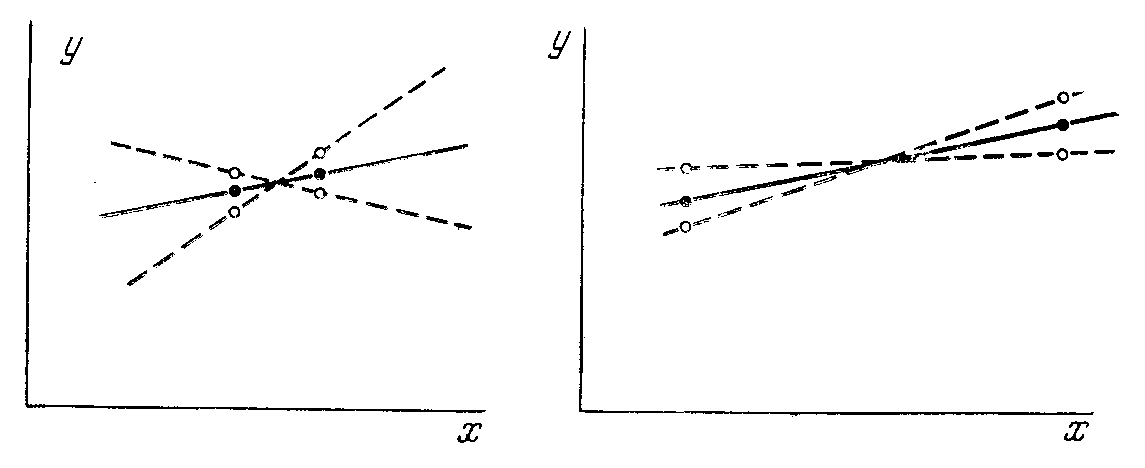 Рис 5.4 Влияние интервала варьирования переменной на точность аппроксимации.
Рис 5.4 Влияние интервала варьирования переменной на точность аппроксимации.
Использование многофакторных планов увеличивает радиус обследуемой сферы за счет свойств многомерного пространства, не увеличивая при этом интервалов варьирования по каждой переменной в отдельности. Это особенно наглядно демонстрируется задачей с тремя переменными (рис 5.5). При варьировании переменных на двух уровнях (-1), (+1) исследуемое пространство ограничивается кубом с вершинами, определяемыми перестановкой чисел (±1, ±1,±1).
Нетрудно рассмотреть, что план, представленный матрицей трехмерного пространства, оказывается заданным координатами точек, которые являются подмножеством вершин куба и образует правильный тетраэдр, или, как считается в математике, правильный симплекс (простейшую фигуру). Сфера, описанная вокруг симплекса, имеет радиус, равный 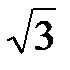 . Распространение этого утверждения на k-мерное пространство приводит к заключению об увеличении радиуса обследуемой поверхности до r=
. Распространение этого утверждения на k-мерное пространство приводит к заключению об увеличении радиуса обследуемой поверхности до r= 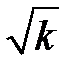 . В частности, в семимерном пространстве r=
. В частности, в семимерном пространстве r= 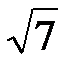 . Таким образом, рост числа независимых переменных увеличивает радиус обследуемой сферы, хотя интервалы варьирования по каждой независимой переменной остаются теми же.
. Таким образом, рост числа независимых переменных увеличивает радиус обследуемой сферы, хотя интервалы варьирования по каждой независимой переменной остаются теми же.
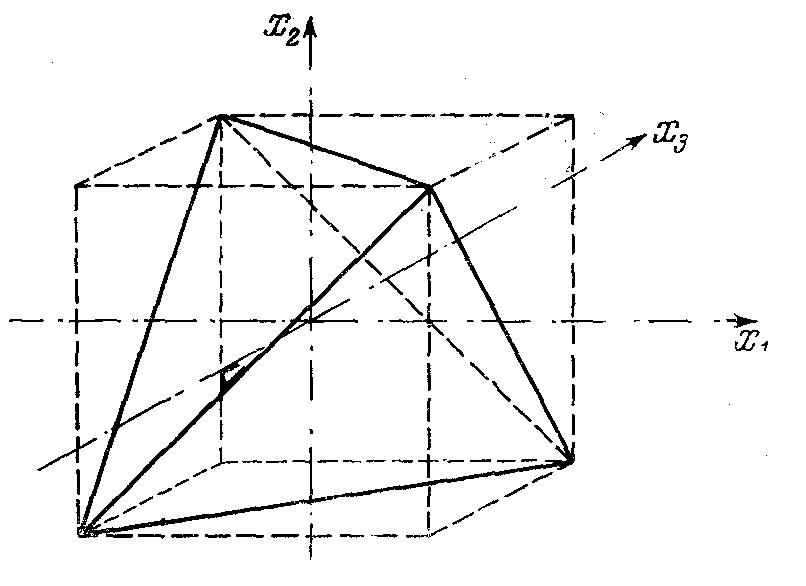
Рис.5.5 Обследуемое пространство существования моделируемого объекта при k=3.
Еще раз остановимся на всех свойствах планов, удовлетворяющих условиям (5.8):
- геометрически они задаются координатами вершин правильных комплексов;
- планы ортогональны – все их коэффициенты регрессии оцениваются независимо друг от друга;
- все коэффициенты регрессии в пространстве размерности k оцениваются одной и той же дисперсией σ2{bi}=σ2{y}/(k+1);
- математиками строго показано, что они выбраны на множестве из всех возможных планов в названной области так, что дисперсия оказывается минимальной;
- все эти планы – ротатабельны, т.е. дисперсия предсказанного значения зависит только от радиуса, проведенного из центра эксперимента;
- информация уравнения регрессии (ее мера 1/σ2{η}), полученная на основании ротатабельного плана, распределена равномерно по сфере с радиусом r.
Свойство ротатабельности особенно важно для исследователя, так как ему неизвестен участок, где располагается точка искомого решения. Такие планы дают ему уверенность, что выбранное решение (скажем, оптимальное) будет обладать той же точностью, которая заложена определением коэффициентов регрессии по опытам выбранного плана экспериментов. Можно сказать, что такие планы оптимальны в широком смысле.
Теперь остановимся на порядке построения таких планов экспериментов. Для этого начнем с планирования плана экспериментов для объекта, поведение которого определяется двумя независимыми переменными, варьируемыми на двух уровнях. При том воздействие каждой из переменных на результат поведения (выход продукции, например) зависит от значения второй. В качестве примера можно рассмотреть воздействие удобрений на урожайность при разной влажности почвы. Это обстоятельство необходимо учитывать в уравнении регрессии через произведение переменных. Такое планирование называется полным факторным экспериментом типа 2к (где 2-число уровней варьирования переменных, а k – число независимых переменных).
При полном фактором эксперименте в рассматриваемом случае уравнение регрессии будет иметь вид:
η=β0+β1х1+β2х2+ β12х1х2.
В нем имеется уже один нелинейный член, β12х1х2. Матрица независимых переменных для полного факторного эксперимента типа 22 представлена ниже. Если до проведения опытов становится известным, что β12=0, то в матрице независимых переменных можно взять вместо х1х2 третью независимую переменную, и она превратится в план для трех независимых переменных.
| х0 | План | ||
| х1 | х2 | х1х2 | |
| +1 | -1 | -1 | +1 |
| +1 | +1 | -1 | -1 |
| +1 | -1 | +1 | -1 |
| +1 | +1 | +1 | +1 |
Это уже будет планирование в трехмерном пространстве. Если на самом деле β12≠0, а мы воспользуемся приведенным планом для трехмерной задачи, то коэффициент b3, оцененный по этому плану, будет оценкой для суммы (β3+β12). Такие оценки называют совместными.
Полный факторный эксперимент типа 23 (с тремя независимыми переменными) описывается уравнением регрессии типа:
η=β0+β1х1+β2х2+β3х3+ β12х1х2+β13х1х3+ β23х2х3+ β123х1х2х3.
Ядром этого плана является полный факторный эксперимент типа 22, взятый для двух переменных х1,х2 (оно выделено в матрице). В плане оно повторено дважды, сначала для х3=-1, а потом для х3=+1, остальные столбцы получаются соответствующим перемножением столбцов х1,х2,х3.
Матрица для экспериментов этого типа требует уже 23=8 опытов:
| План | |||||||
| х0 | х1 | х2 | х3 | х1х2 | х1х3 | х2х3 | х1х2х3 |
| +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 |
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 |
| +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 |
| +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 |
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 |
| +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 |
| +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 |
Если приходится строить план типа 24, то дважды повторятся планы типа 23 (один для х4=-1, а второй для х4=+1) с последующим вычислением остальных столбцов через первые четыре столбца.
Легко заметить, что матрица полного факторного эксперимента при k=3 использована нами для семи независимых переменных при отсутствии парных и тройного взаимодействия в плане типа 23. Кроме того, план типа 23 состоит из двух планов для трех независимых переменных без парных и тройного взаимодействия (один взят со знаком плюс, а другой со знаком минус).
Дата добавления: 2015-11-12; просмотров: 1130;
