Оптимизация задач при линейном программировании
Задачами линейного программирования называются оптимиза -ционные задачи, в которых ограничения в виде равенств или неравенств и целевая функция (оптимизируемая) - линейны. Методы линейного программирования широко используются для решения различных военных, экономических, промышленных и организационных задач. Линейное программирование представляет собой наиболее часто используемый метод оптимизации (74% общего числа методов оптимизации).
В основном в таких задачах требуется ответить на вопрос: как распорядиться ограниченными ресурсами, чтобы добиться наибольшего эффекта.
В стандартной или канонической форме с m ограничениями и n переменными она имеет следующий вид:
Максимизировать или минимизировать
z=c1x1+c2x2+…+cnxn
при ограничениях
a11x1+a12x2+…a1nxn=b1,
………………………
………………………
am1x1+am2x2+…+amnxn=bm,
x1≥0, х2≥0,…хn≥0,
b1≥0, b2≥0,…bm≥0.
И в других формах записи:
a) 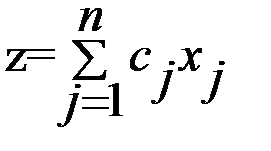 , j
, j 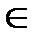 (1,2…n),
(1,2…n),
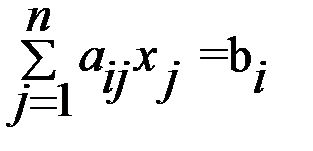 , i
, i 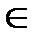 (1,2…m),
(1,2…m),
xj ≥0, bi ≥0, m<n,
б) Z=CX, AХ=B, X≥0, B≥0,
где А – матрица размерности m  n; B – вектор столбец размерности m
n; B – вектор столбец размерности m  1, а C – вектор строка размерности 1
1, а C – вектор строка размерности 1  n, Х – вектор (столбец) переменных (другое их название соответственно: матрица коэффициентов, вектор ресурсов, вектор оценок задачи, вектор переменных).
n, Х – вектор (столбец) переменных (другое их название соответственно: матрица коэффициентов, вектор ресурсов, вектор оценок задачи, вектор переменных).
Стандартность записи задачи линейного программирования состоит в том, что в представленном виде она готова к использованию методов решения системы линейных алгебраических уравнений.
Не все сформулированные задачи линейного программирования имеют стандартную (каноническую) форму. Чаще всего ограничения имеют вид неравенств, и некоторые переменные могут иметь только неотрицательные значения. Таким образом, первый этап решения задачи линейного программирования состоит в приведении ее к стандартной форме.
Преобразование неравенств. Ограничения в виде неравенств преобразуются в равенства при помощи избыточных (остаточных) переменных. Например, неравенство вида
х1+2х2+3х3+4х4+х5≤25
можно преобразовать в равенство при помощи остаточной переменной х5:
х1+2х2+3х3+4х4+х5=25.
Переменная х5 неотрицательна. При обратном неравенстве в рассматриваемом линейном уравнении перед остаточной переменной ставится знак минус. Дополнительные (остаточные) переменные так же необходимы, как и исходные переменные задачи. Они могут принимать только положительные значения, а их значения в оптимальном решении позволяют судить о том, являются ли ограничения в виде неравенств активными.
Преобразование неограниченных по знаку переменных. Поскольку переменные задач линейного программирования в стандартной форме предполагаются неотрицательными, неограниченные по знаку следует заменять разностью двух неотрицательных переменных. Например, если xj – неограниченная по знаку переменная, то используется следующая замена переменных (при n – компонентном векторе переменных): xj=xn+1–xn+2, где xn+1, xn+2 – неотрицательные дополнительные переменные. Знак xj зависит от числовых значений дополнительных переменных.
Пример приведения задачи линейного программирования к стандартной форме: минимизировать z=x1-2x2+3x3 при ограничениях:
x1+x2+x3≤7,
x1-x2+x3≥2,
3x1-x2-2x3= –5,
x1,x2>0,
где х3 переменная, не ограниченная по знаку.
Решение:
1. Заменим х3 на х4-х5, где х4,х5>0.
2. Умножим обе части третьего уравнения на (-1).
3. Введем дополнительные (остаточные) переменные х6 и х7 в первые два ограничения.
4. Целевая функция при этом не меняется, так в нее х6 и х7 входят с нулевыми коэффициентами.
Рассматриваемая задача равносильна следующей задаче линейного программирования в стандартной форме:
минимизировать z=x1-2x2+3x4-3x5,
при ограничениях x1+x2+x4-x5+x6=7,
x1-x2+x4-x5-x7=2,
-3x1+x2+2x4-2x5=5,
x1,x2,x3,x4,x5,x6,x7≥0.
В матричных обозначениях: минимизировать Z=CХ при ограничениях АX=B, Х≥0.
Определения, касающиеся этой задачи:
1. Допустимое решение - неотрицательный вектор Х, для которого выполняется ограничение АХ=В.
2. Допустимая область – совокупность всех допустимых решений. Если допустимая область пуста, то система называется противоречивой (несовместной).
3. Оптимальное решение задачи соответствует оптимальному значению целевой функции.
4. Не единственность оптимального решения - наличие нескольких допустимых решений при оптимальном значении целевой функции.
5. Единственность оптимума – наличие одного решения, соответствующего оптимальному значению целевой функции.
6. Неограниченный оптимум – отсутствие конечного оптимума. 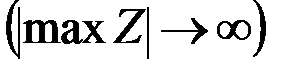
Каждое из неравенств, образующее математическую модель линейного программирования, определяет некоторое полупространство n-мерного пространства (n – число переменных), а все вместе – некоторую область Ω в нем, являющуюся пересечением конечного числа полупространств. Полупространства - выпуклые множества, их пересечение тоже выпукло, т.е. оно является выпуклым «многогранником». Число вершин его ограничено.
Теоретические разработки по линейному программированию указывают, что число решений (базисных) задач линейного программирования равно числу вершин «многогранника». При большой размерности n перебрать все возможные решения затруднительно, поэтому отыскание оптимального решения надо начинать с одного определенного базисного решения.
Особенность применения симплекс-метода при оптимизации задач линейного программирования состоит как раз в этом: отыскивается одна из вершин «многогранника» (одно базисное решение, называемое опорным), а потом осуществляется переход к другим путем исследования возможного изменения в нужную сторону целевой функции при замене перспективных свободных переменных на базисные.
Алгоритм симплекс метода при оптимизации задачи линейного программирования:
1. Нахождение начального допустимого базисного решения.
2. Переход от начального решения к другому допустимому базисному решению с лучшим значением целевой функции.
3. Продолжение поиска допустимых базисных решений, улучшающих значение целевой функции
Демонстрировать этот алгоритм лучше всего на конкретном примере. Минимизировать функцию z=x4-x5→min, если уже известен начальный допустимый базис:
x1=1-x4+2x5,
x2=2+2x4-x5,
x3=3-3x4-x5,
x1,x2,x3,x4,x5≥0.
Соответствующий ему опорный план будет (1,2,3,0,0), а целевая функция z=0. Исходная целевая функция свидетельствует о возможности снижения за счет увеличения небазисного переменного x5. Увеличение х5 не может перевести х1 и х2 в отрицательные значения (это видно из первого равенства), а из двух последующих следует, что возможно увеличение х5 до 2. Тогда при сохранении х4=0, х3 оказывается равным 1 (положительному числу), а х2=0, х1=5. Новый опорный план –(5;0;1;0;2), а 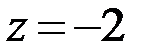 . Для перестройки исходной системы ограничений необходимо выразить новые базисные переменные через х2, х4 (небазисные):
. Для перестройки исходной системы ограничений необходимо выразить новые базисные переменные через х2, х4 (небазисные):
x5=2+2x4-x2 (из второго ограничения),
x1=1-x4+2(2+2x4-x2) (из первого ограничения),
x3=3-3x4-(2+2x4-x2) (из третьего),
z=x4-(2+2x4-x2).
Теперь задача приводится к виду:
x1=5+3x4-2x2,
x3=1-5x4+x2,
x5=2+2x4-x2,
xi≥0, (i=1,2,3,4,5),
z=-2-x4+x2→min.
Исследование целевой функции на возможность ее снижения указывает, что это можно сделать только за счет увеличения x4 при сохранении х2=0. При этом первое и третье ограничения ничуть не препятствуют этому, а второе допускает увеличение x4 до 1/5. При этом x4=1/5, х2=0, а из второго ограничения следует, х3=0, из первого x1=28/5, а из третьего – х5=12/5. Новый опорный план (28/5;0;0;1/5;12/5), ограничения, соответствующие ему, через небазисные х2, х3:
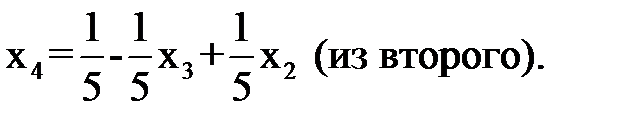
Подстановка этого значения в два других ограничения дает:
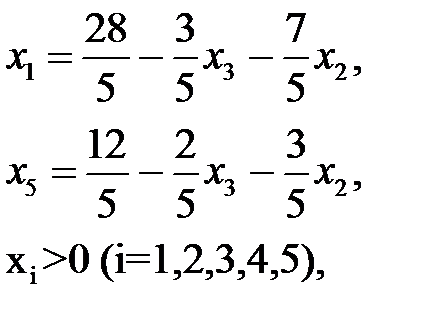
Целевая функция при этом опорном плане:
z=-2-( 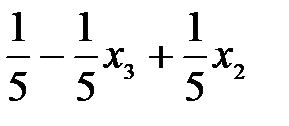 )+х2,
)+х2,
или
z=- 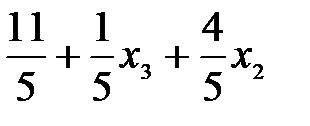 .
.
В ней обе небазисные переменные входят с положительным знаком, поэтому за счет них уменьшения целевой функции достигнуть невозможно, поэтому последний опорный план является решением задачи линейного программирования (при 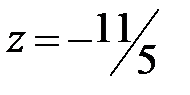 ).
).
Формализация симплексного метода оптимизации задач линейного программирования осуществляется с помощью уже изученных симплекс-таблиц. В них переписываются не только коэффициенты при переменных ограничений и их свободные члены, но и коэффициенты целевой функции, переписанной в виде z-L=0, где L - стандартная запись целевой функции (знаки коэффициентов при переменных целевой функции меняются на обратные, а ее свободный член берется равным нулю). Продемонстрируем это на конкретном примере:
Минимизировать целевую функцию
z=x2-3x3+2x5
при ограничениях x1+3x2-x3+2x5=7
-2x2+4x3+x4=12
-4x2+3x3+8x5+x6=10,
xi≥0, (i=1,…,6).
Задача уже приведена к стандартной канонической форме. Ее можно представить и в другой форме, позволяющей сразу определить опорный план (исходное базисное решение):
x1=7-3x2+x3-2x5,
x4=12+2x2-4x3,
x6=10+4x2-3x3-8x5,
xi≥0 (i=1,…,6).
Исходный опорный план (7,0,0,12,0,10), а целевая функция
z -x2+3x3–2x5=0.
Симплекс – таблица исходной системы при новой записи целевой функции:
| Базисные переменные | x1 | x2 | x3 | x4 | x5 | x6 | Свободные члены | |
| x1 | (7) | -1 | ||||||
| x4 | (12) | -2 | ||||||
| x6 | (10) | -4 | ||||||
| z | -1 | -2 | ||||||
| x1 | (10) | 5/2 | 1/4 | |||||
| x3 | (3) | -1/2 | 1/4 | |||||
| x6 | (1) | -5/2 | -3/4 | |||||
| z | 1/2 | -3/4 | -2 | -9 | ||||
| x2 | (4) | 2/5 | 1/10 | 4/5 | ||||
| x3 | (5) | 1/5 | 3/10 | 2/5 | ||||
| x6 | (11) | -1/2 | ||||||
| z | -1/5 | -4/5 | -12/5 | -11 |
В строке целевой функции (z) нет положительных элементов. Значит, полученное решение будет оптимальным: (0;4;5;0;0;11), а целевая функция равна (-11).
И еще одна оптимизация с иным ответом: минимизировать целевую функцию: z=2x1-3x4+x5+2x6
при ограничениях
x1+x2-3x4+2x6=5,
2x2-3x3+x4+x5=4,
-3x1-x2+2x3-x5=-3,
xi≥0 (i=1,…,6).
Умножив на (-1) третье ограничение, получим систему в стандартной форме и запишем коэффициенты ограничений целевой функции (с обратными знаками), а также свободные члены в первый шаг симплекс-таблицы.
Проведем соответствующие преобразования.
| Базисные переменные | x1 | x2 | x3 | x4 | x5 | x6 | Свободные члены | |
| -3 | 0 | |||||||
| -3 | ||||||||
| -2 | ||||||||
| z | -2 | -1 | -2 | |||||
| 1/2 | 1/2 | -3/2 | 5/2 | |||||
| -3 | ||||||||
| -2 | ||||||||
| z | -1 | -1 | ||||||
| 1/2 | 7/2 | 9/2 | 3/2 | 17/2 | ||||
| -3 | ||||||||
| -2 | ||||||||
| z | -1 | -1 | ||||||
| (4) | х6 | -4 | -3/2 | |||||
| (1) | х4 | -3 | -1 | |||||
| (3) | х5 | -2 | ||||||
| z | -2 | |||||||
| (2) | х6 | 1/2 | -2 | |||||
| (1) | х2 | -3 | -1 | |||||
| (2) | х5 | -1 | -1 | |||||
| z | -2 | |||||||
| х6 | 5/6 | -5/3 | -1/3 | 4/3 | ||||
| х2 | -3/2 | 1/2 | 1/2 | |||||
| х1 | -1/6 | -1/6 | 1/6 | 1/3 | ||||
| z | 4/3 | -2/3 | -4/3 | 10/3 | ||||
| х3 | -2 | -2/5 | 6/5 | 8/5 | ||||
| х2 | -5/2 | -1/10 | 9/5 | 22/5 | ||||
| х1 | -1/2 | 1/10 | 1/5 | 3/5 | ||||
| z | -4/5 | -8/5 | -6/5 |
В столбце с положительным коэффициентом целевой функции z (это +2) нет положительных элементов. Значит, функция не ограничена по минимальному значению.
В общем случае решение задач линейного программирования зависит от знаков z – строки симплекс-таблицы (при записи этих коэффициентов в нее в виде z-L=0):
1. При всех неположительных коэффициентах z-строки задача решена, оптимизация достигнута.
2. При наличии положительных коэффициентов в z-строке:
○ задача не имеет решения, если над каждым положительным коэффициентом z-строки находится только отрицательные или нулевые элементы;
○ если положительные элементы имеются, то выбирается разрешающий элемент и производится преобразование симплекс-таблицы (при этом допускается произвольный выбор разрешающего столбца из нескольких переменных).
Все представленное в этом подразделе свидетельствует о высокой алгоритмизации методов оптимизации задач линейного программирования с помощью симплекс-таблиц. Использование этих алгоритмов в ЭВМ не только позволяет быстро получить решения задач, но и исключает возможность принятия по ним ошибочных управленческих решений.
Опыт решения большого числа практических задач показывает, что число итераций (шагов) при решении задач линейного программирования в стандартной форме с m ограничениями и n переменными лежит в пределах m…3m, при среднем значении 2m. Время, требуемое для решения, приблизительно пропорционально кубу числа ограничений (m3).
Число ограничений задачи, оказывается, в большей мере влияет на эффективность вычисления, чем число переменных, поэтому следует отбрасывать излишние ограничения при разработке модели.
Дата добавления: 2015-11-12; просмотров: 1389;
