Методика решения систем линейных алгебраических

Системы линейных алгебраических уравнений представляются в форме:

Такая система удобно записывается и в другой (матричной) форме:

AХ=B,

где А – матрица коэффициентов, содержащая m строк и n столбцов:

, (4.2)

а Х и b – векторы,

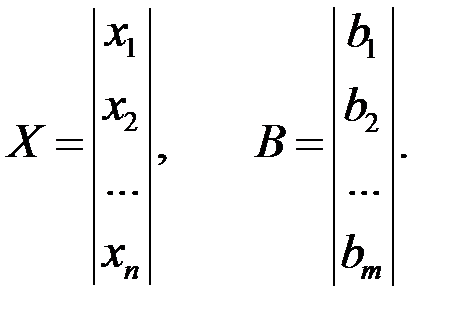
Решением этой системы уравнений является совокупность таких значений неизвестных х₁=α₁, х₂=α ₂, …,x_n=α _n, которая удовлетворяет всем уравнениям системы (4.1).

Если система имеет хотя бы одно решение, то она называется совместной, если не имеет решения, то несовместной. Совместная система, имеющая одно решение, называется определенной, и неопределенной, если она имеет бесконечное множество решений.

Две системы уравнений типа (4.1) с одними и теми же неизвестными называются равносильными, если каждое решение одной из них является решением другой или если они обе несовместны (в последнем случае число уравнений может быть даже разным).

При любых преобразованиях системы при нахождении решений получающиеся системы должны быть совместны первоначальной.

Матрица А называется матрицей системы. Если же к ней добавить столбец b, то полученная матрица будет расширенной матрицей системы B.

Равносильность системы согласно теоремам линейной алгебры сохраняется при следующих преобразованиях расширенной матрицы B:

○ взаимной перестановке двух строк в расширенной матрице B;

○ умножении какой-либо строки на любое число, не равное нулю;

○ при прибавлении к какой-либо строке любой другой строки, умноженной на любое число, не равное 0;

○ при выбрасывании из системы нулевой строки (уравнения типа 0=0).

Ступенчатая матрица - это матрица, у которой все элементы, расположенные ниже главной диагонали матрицы А(а₁₁ а₂₂…а_mn) равны нулю.

4.2 Способы решения систем линейных алгебраических уравнений.

Самой простой (можно сказать идеальной) системой линейных алгебраических уравнений является система, в которой число уравнений равно числу компонентов вектора переменных, т.е. при m=n.

Общий метод решения невырожденных систем, т.е. систем с определителем их матриц, не равным нулю, опирается на формулу Крамера:

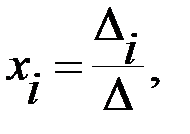i=1,2…n. (4.3)

Здесь ∆_i=det A', определитель матрицы, получаемой заменой i-того столбца матрицы А столбцом свободных элементов матрицы В.

Формулы (4.3) дают решение системы (4.1) при m=n в явном виде. В общем случае (при любом n) они в вычислительном плане малоэффективны: требуют большого числа операций и очень чувствительны к ошибкам округления. Уже при n=20 требовалось 4,5×10¹⁹ умножений, которые машина при производительности в 1 млн. операций в секунду, производила бы 1,4×10⁶ лет.

На практике используются другие методы, которые целенаправленным преобразованием исходной расширенной матрицы резко уменьшают число вычислительных операций.

Метод Гаусса (метод «лидеров») можно считать универсальным, так как он не только обеспечивает получение решения за конечное (разумное) число действий, но и может использоваться не только при m=n. Алгоритм (словесный) этого решения включает четыре ступени:

○ составление расширенной матрицы системы (4.1) В;

○ приведение матрицы В к ступенчатому виду;

○ запись равносильной ступенчатой системы алгебраических уравнений по ступенчатой расширенной матрице;

○ решение ступенчатой системы уравнений снизу вверх.

Ступени 1, 2 и 4 не представляют особых трудностей. Только преобразование расширенной матрицы к ступенчатому виду требует особой внимательности. Оно проводится в следующем порядке:

○ отыскание лидеров (первых элементов строк, заведомо не равных нулю). Они найдутся обязательно (ведь мы рассматриваем невырожденную систему, в случае необходимости мы можем переставить уравнения в системе);

○ составление отношений для первого шага преобразования матрицы

(4.4)

○ прибавление к элементам каждой строки после первой (i=2.3…n) элементов первой строки, умноженной на соответствующее ей соотношение (4.4), этим самым мы исключаем переменную х₁ из всех уравнений, кроме первого, и получаем расширенную матрицу следующего вида:

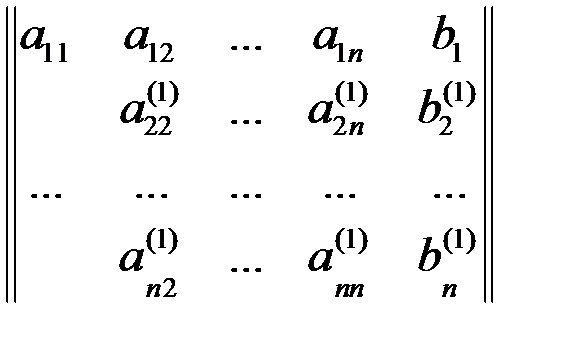
○ отыскание лидера на втором шаге, составление отношений для него и устранение из матрицы переменного х₂, для всех строк кроме второй. Остальные шаги являются повторением предыдущего пункта.

После (n-1) шага расширенная матрица (при m=n) примет вид:

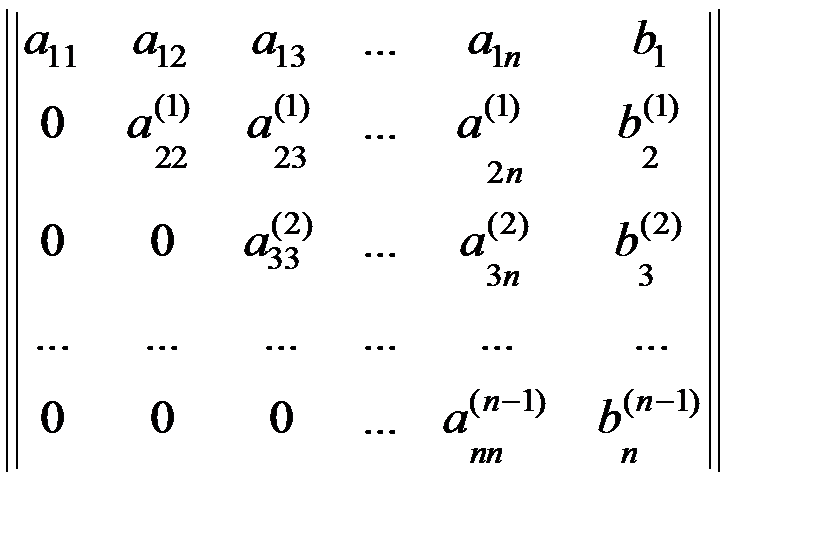(4.5)

На этом заканчивается третья ступень при использовании метода лидеров. По ступенчатой матрице (4.5) записывается равносильная система уравнений исходной:

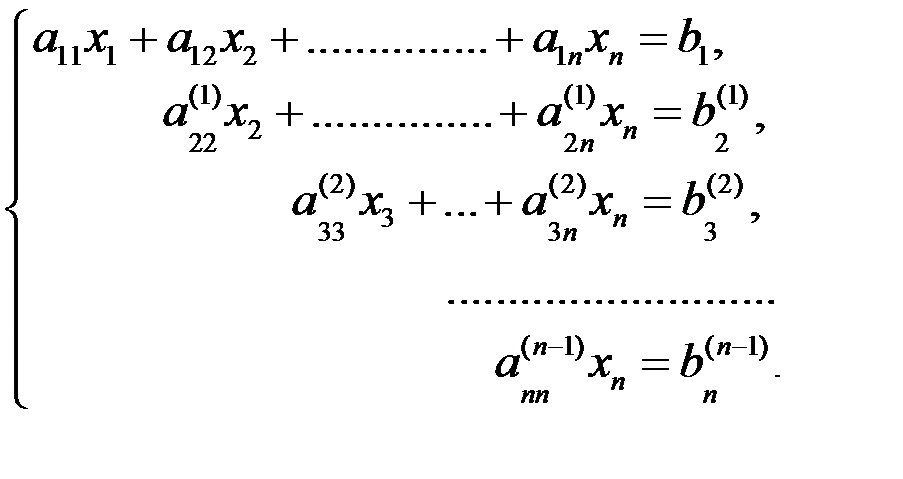(4.6)

Система (4.6) легко решается путем получения каждого предыдущего элемента через последующий, начиная с последнего.

В случае, если в исходной системе m<n, равносильная ступенчатая система уравнений примет после аналогичных преобразований следующий вид:

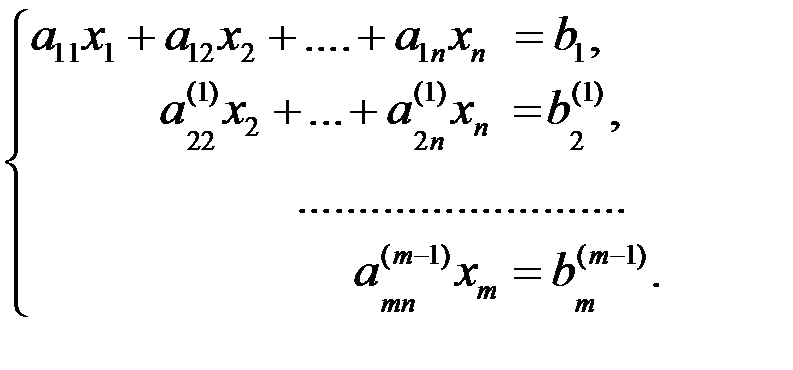
(4.7)

Это будет только в том случае, если среди m уравнений не найдется ни одного уравнения типа 0=0. Если же окажется, что среди исходных уравнений были такие, то лидеров окажется меньше числа уравнений, например r<m<n (к₁<к₂<…<к_r). Переменные, соответствующие им, называются базисными, а остальные, если они есть (s₁<s₂<…<s_φ), свободными. Тогда система (4.1) будет равносильной ниже следующей:

)

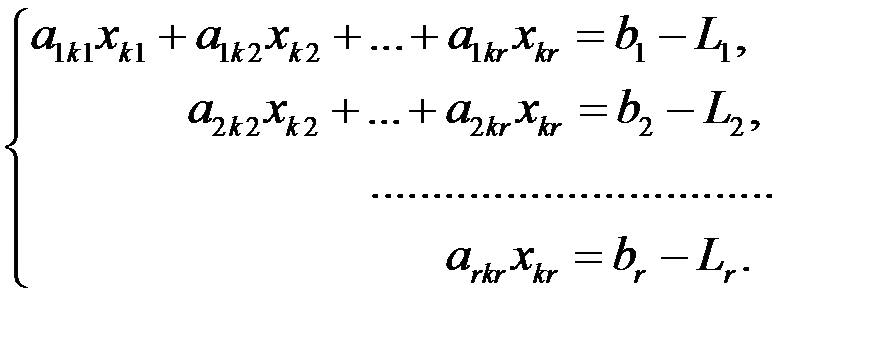В ней все a_iki отличны от нуля, а через L_i обозначена сумма свободных неизвестных, умноженных на стоящие перед ними коэффициенты i-того уравнения.

Эта ступенчатая система дает общее решение системы (4.1):

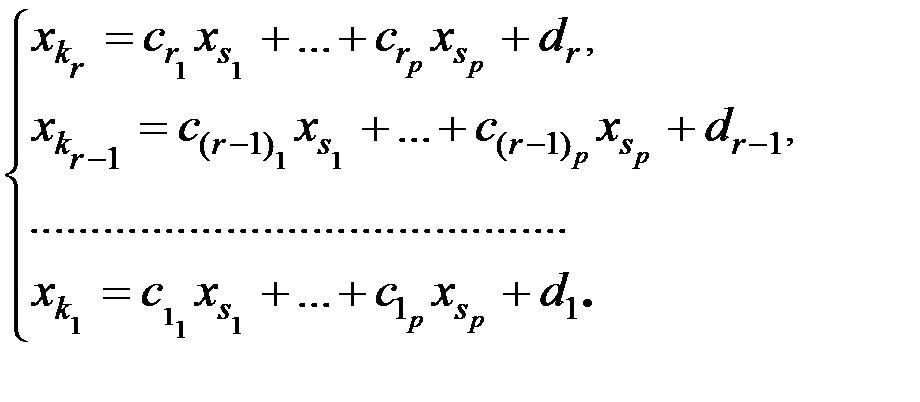
Частные решения получаются при произвольных значениях свободных переменных. При равенстве всех свободных переменных нулю, получаем базисное решение.

Общие выводы по анализу решения методом Гаусса:

○ Система несовместна (т.е не имеет решений), если в системе имеется строка, в которой лидер (первый элемент, не равный нулю) стоит на последнем месте (т.е. им является свободный член соответствующего уравнения);

○ Система совместна (т.е. имеет решение, одно или несколько), если в расширенной ступенчатой матрице нет строки с лидером на последнем месте.