Качественное исследование математических моделей.

3.4.1. Методы исследования ММ на полноту, непротиворечивость и корректность, существование и единственность решений.

Разобранная задача может быть решена и для частного случая закона нагружения рабочих органов сельскохозяйственного орудия R=f(t) с целью определения возможного взаимного смещения трактора и сельхозмашины (СХМ). В этом случае математическая модель будет представлена обыкновенным дифференциальным уравнением второго порядка колебаний СХМ относительно трактора:

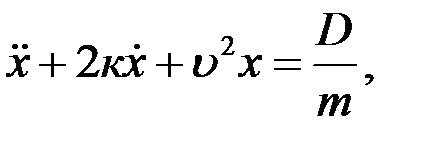(3,4)

где х - перемещение сельскохозяйственной машины относительно трактора; к - коэффициент, характеризующий силы сопротивления колебаниям в обрабатываемом материале; D - обобщенная возмущающая сила.

Математическая модель даже в таком виде может создать проблемы при ее исследовании (например, при переменной жесткости упругого элемента или нарушении непрерывности обобщенной силы).

И большинство технических задач в своей основе описываются обыкновенными дифференциальными уравнениями второго порядка или даже более высокого порядка. Все они могут быть сведены к системам обыкновенных дифференциальных уравнений первого порядка. Многочисленность уравнений в таких системах не позволяет априорно сделать предсказание о возможности решения рассматриваемой системы.

Заключение о возможности решения систем дифференциальных уравнений первого порядка может быть произведено на основе исследования ее на корректность (соответствие физическим и другим законам, которые определяют поведение объекта), на полноту, существование и единственность решения, на устойчивость к возмущениям входных переменных. Причем это исследование должно проводиться при наличии дополнительных условий: начальных, краевых или граничных.

Полной математическая модель, представленная системой дифференциальных уравнений

х'₁=f₁(t,x₁,x₂,…,x_n),

х'₂=f₂(t,x₁,x₂,…,x_n), (3.5)

……………………..

х'_n=f_n(t,x₁,x₂,…,x_n),

считается тогда, когда в ней учтены все значащие факторы (переменные) и все дополнительные условия. Последние указывают значения переменных для одного состояния (начальные условия) или нескольких (краевые, граничные условия). В такой форме математическая модель в обыкновенных дифференциальных уравнениях первого порядка носит название задачи Коши. В других ММ дополнительные условия включают и ограничения, накладываемые на переменные состояний.

Основным заданием задачи Коши является отыскание решения в виде вектора х₁(t), х₂(t),... х_n(t), который обращает в тождества уравнения модели (3.5) при дополнительных условиях.

В теории дифференциальных уравнений теорема существования и единственности решения являются определяющей.

Теорема существования и единственности решения задачи Коши. Пусть в системе дифференциальных уравнений

х'_i=f_i(t,x₁,x₂,…,x_n), i=1,2,…n

все функции f_i=(f₁, f₂,…, f_n) удовлетворяют условиям:

1) они непрерывны в некоторой замкнутой области D пространства с координатами t,x₁,x₂,…,x_n, определяемой неравенствами

t₀-a≤t≤t₀+a, x_i0-b_i≤ х_i ≤ х_i0+b_i i=1,2,…n,

а следовательно, и ограничены │f_i│<M;

2) все они в области D удовлетворяют условию Липшица:

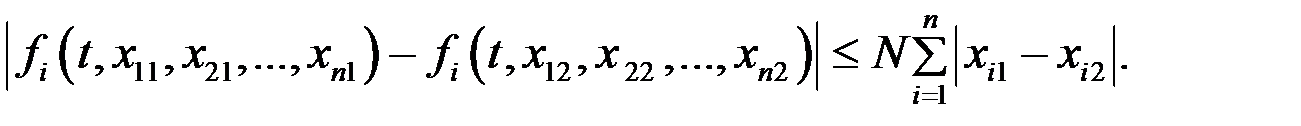
Тогда в окрестности точки t₀ существует единственное решение

х₁(t), x₂(t),..., x_n(t) системы, удовлетворяющее начальным условиям

x_i(t₀) =x_i0, и оно определено на отрезке t₀-h<t₀<t₀+h, где h≤мин(a, b₁/М, b₂/М,..., b_n/М).

Математики строго доказали эту теорему: в ней первое условие - условие достаточности существования решения, второе - условие единственности его.

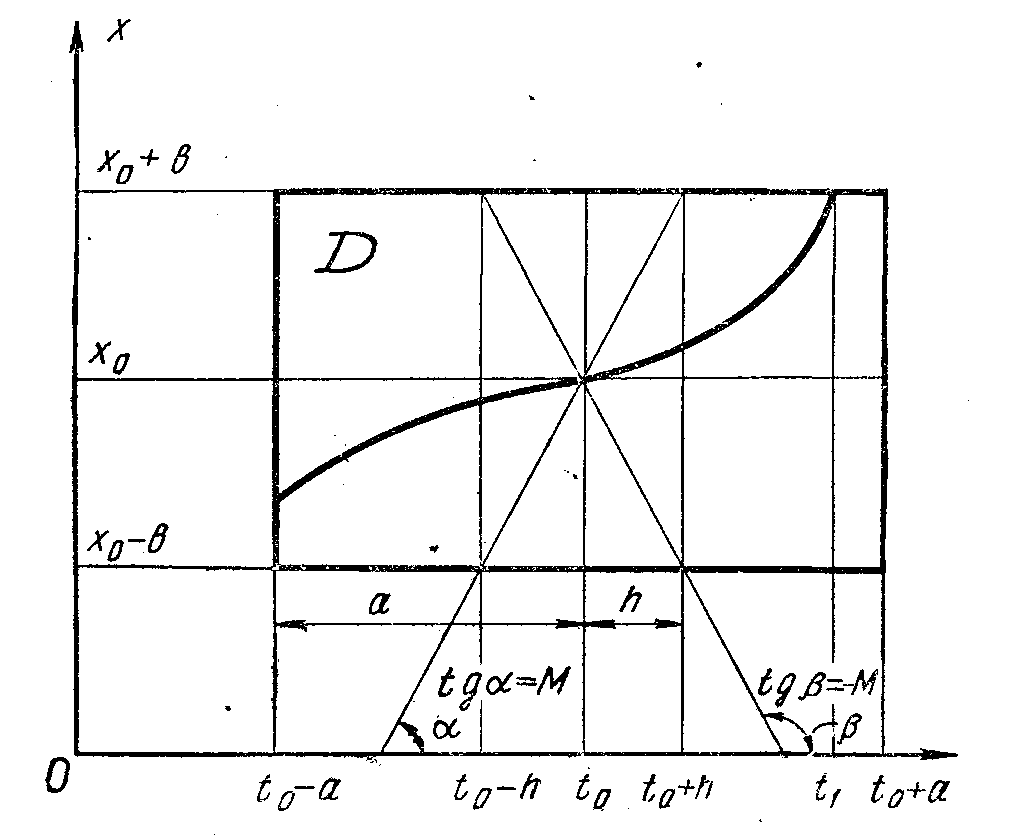
Рис. 3.4. Область существования и единственности решения

одномерной модели в дифференциальных уравнениях.

Условие Липшица всегда будет удовлетворяться, если частные производные каждой из функции по всем входящим в нее переменным ограничены по модулю в области D:

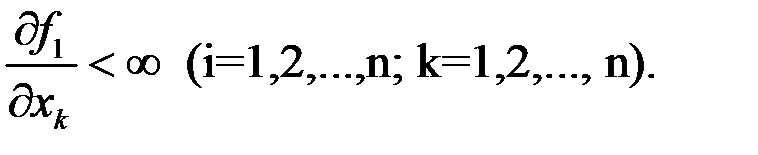
Указанное условие является легко проверяемым, а значит, наиболее приемлемым в практике использования математических моделей. Для одномерной модели область существования и единственности решения при заданных в теореме условиях в декартовых координатах имеет вид, показанный на рис.3.4.

3.4.2.Методы исследования ММ на устойчивость и колебательность.

В простейшем случае понятие устойчивости системы связано со способностью возвращаться в состояние равновесия после исчезновения действия внешних сил, которые вывели ее из этого состояния.

Опыт показывает, что некоторые положения равновесия системы устойчивы к небольшим возмущениям, а другие - неустойчивы (рис.3.6).

Устойчивое Неустойчивое Безразличное

положение положение положение

Рис 3.6. Виды равновесия.

Понятие устойчивости можно распространить и на общий случай, когда в качестве невозмущенного состояния системы рассматривается не положение ее равновесия, а ее движение по некоторой наперед заданной траектории.

Пусть y*₁(t), y*₂(t),...,y*_n(t) - законы изменения независимых координат невозмущенного движения. Внешние воздействия деформируют его. Действительное движение с координатами y₁(t), y₂(t),...,y_n(t) - называется возмущенным движением. Заданное невозмущенное движение будет устойчивым, если после приложения внешних сил (возмущений), которые затем снимаются, возмущенное движение по истечении некоторого времени войдет в заданную область │у_i(t)-y*_i(t)│≤ε_i, где ε_i – постоянные заданные величины (i =1,2,..n). Начальные значения отклонений называют возмущениями. Ляпуновым А.М. было дано следующее определение устойчивости:

Невозмущенное движение называют устойчивым по отношению переменных х_i, если при всяком произвольно заданном положительном числе ε, как бы мало оно не было, можно выбрать другое такое положительное число δ(ε), что при всех возмущениях x_i0, удовлетворяющих условию и при любом t>t₀ будет выполняться неравенство 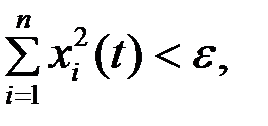в противном случае движение неустойчиво.

При достаточно малых возмущениях устойчивость невозмущенного движения практически означает совпадение его в пределах δ с невозмущенным движением. Несмотря на ограничения, вводимые определением устойчивости по А.М.Ляпунову (возмущения накладываются только на начальные условия, устойчивость рассматривается на бесконечно большом промежутке времени, возмущения предполагаются малыми), оно является плодотворным для практических задач.

При известных общих решениях дифференциальных уравнений можно аналитически решать вопрос о величине отклонений при малых возмущениях и устойчивости возмущенного движения.

При использовании методов приближенного вычисления на ЭВМ информация об устойчивости должна предшествовать самому решению во избежание сбоев машины. В этом случае исследование устойчивости движения (решения) осуществляется с помощью методов, основанных на качественном анализе дифференциальных уравнений возмущенного движения, которым удовлетворяют отклонения х.

Согласно определению возмущенного движения его дифференциальное уравнение имеет вид:

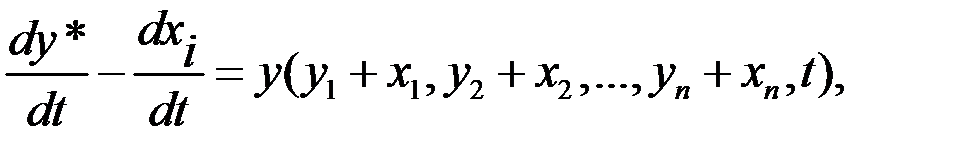
где y*_i - изменение i-той координаты невозмущенного движения; x_i- -отклонение i-той координаты при возмущенном движении.

Допустив разложение правой части уравнения в ряд Тейлора по степеням х_i и пренебрежение членами со степенями х_i выше первой, получим линейные дифференциальные уравнения возмущенного движения в виде:

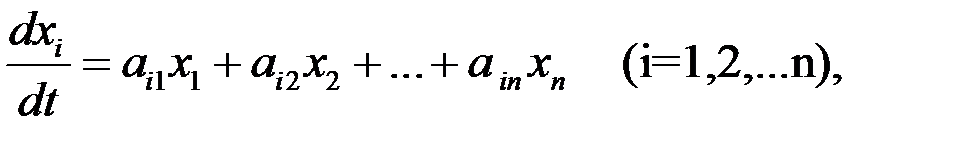
в автоматике называемые уравнениями первого приближения, в которых

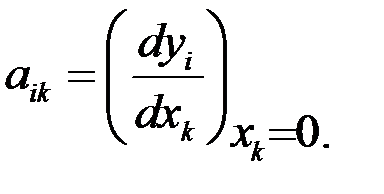
Характеристическое уравнение системы имеет вид

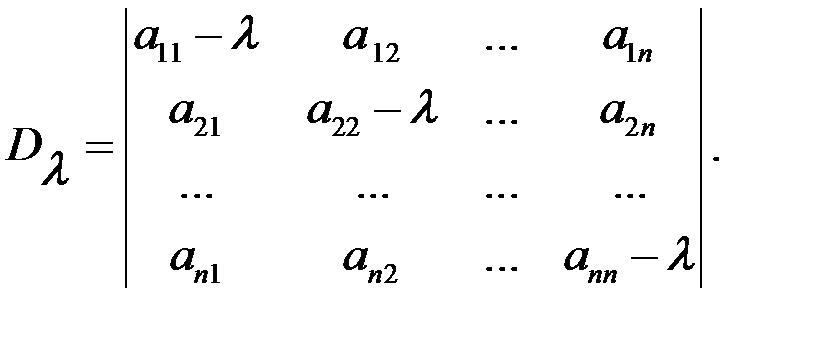
Корни этого уравнения λ_i в общем случае выражаются комплексными числами λ=α_i+jω_i (вещественные и мнимые части корней α_i, ω_i).

Теоремы А.М. Ляпунова об установлении устойчивости по характеристическому уравнению формулируются следующим образом:

1) невозмущенное движение асимптотически устойчиво при отрицательных вещественных частях всех корней λ;

2) невозмущенное движение неустойчиво при наличии хотя бы одного корня с положительной вещественной частью.

При наличии одного или нескольких нулевых корней вопрос об устойчивости движения может быть решен только с помощью анализа исходного уравнения.

Вычисление корней характеристического уравнения степеней выше четвертой аналитическим путем невозможно, поэтому в этом случае используют правила, которые позволяют определять устойчивость системы без вычисления корней - путем использования критериев устойчивости. Критерии устойчивости разделяют на алгебраические и частотные.

Алгебраические критерии строятся на анализе знаков характеристического уравнения: критерии Рауса, Гурвица, Льенера-Шепара (п > 5).

Частотные критерии являются графическими (критерии Михайлова, Найквиста), требуют тоже большой вычислительной работы.

В системах автоматического регулирования приходится решать задачи качества переходных процессов - быстродействия, колебательности, перерегулирования, характеризующих точность и плавность их протекания. Показатели качества, определяемые непосредственно по кривой переходного процесса, называют прямыми оценками. Часто это связано с большими трудностями, поэтому используют косвенные оценки качества.

Методики оценки качеств переходных процессов тоже нельзя отнести к простым вычислительным операциям, но при отсутствии ЭВМ они значительно упрощают решение системы дифференциальных уравнений, составляющих основу математической модели.

Понятие устойчивости решения зависит от специфики рассматриваемой задачи. При проведении исследований исследователю необходимо продумывать возможные случаи сбоя решения.

В книге Тихонова А.Н. и Костомарова Д.П. приведен пример о возможности нарушения устойчивости решения системы линейных алгебраических решений за счет округлений получаемых расчетных данных ЭВМ при использовании плавающей запятой (с пятью значащими цифрами).

При решении системы методом Гаусса

она последовательно приводилась сначала к виду:

а потом к ступенчатому

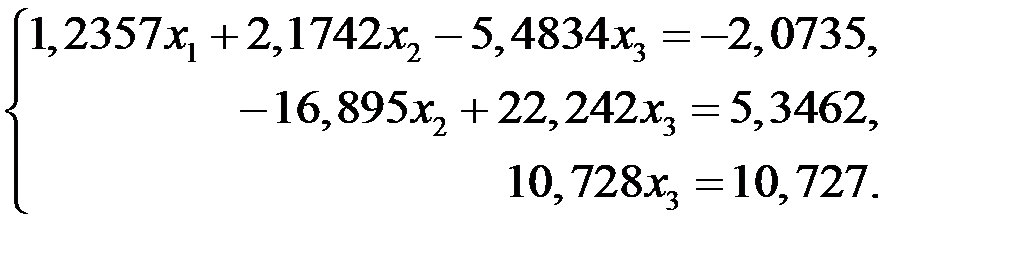
Решение последней системы дало х₁=0,99968, х₂=0,99994, х₃=0,99991.

Этот результат близок к точному х₁=х₂=х₃=1. При перемене мест второго и третьего уравнений в промежуточной (второй) записи системы и приведения полученной системы к ступенчатой записи получено

Откуда х₁=2,9021, х₂=1,4286, х₃=0,9992.

Сравнение полученных данных свидетельствует о зависимости получаемого решения от порядка расположения уравнений в системе. Причина такой значительной разницы в решениях легко выявляется. Все неприятности связаны с малым значением ведущего элемента второго шага (0,0007) и соответственно с большим коэффициентом пересчета третьего уравнения (24136), что и приводит в большой вычислительной ошибке.

Для избегания такого сбоя в счете устанавливают приемлемый порядок выбора ведущего элемента на каждом шаге. Простейший порядок выбора состоит в следующем. Перед началом нового шага исключения переменного сравниваются элементы столбца с исключаемым переменным и уравнение с бóльшим переносится на ведущую позицию (в рассматриваемую строку матрицы).

Любая специальная программа усложняет алгоритм счета, но способствует повышению точности решения.