Основные этапы математического моделирования

Использование результатов математического моделирования как средства решения сложных прикладных задач и проблем имеет в каждом конкретном случае специфические особенности. Однако общие черты всего процесса исследования позволяют выделить в этой работе пять этапов.

1. Построение физической модели. Поскольку физическая модель строится (формулируется) как некоторое приближение к исходному объекту, то она оказывается всегда проще самого объекта.

Физическая модель формулируется на языке той науки, к которой относится реальный объект исследования, с помощью абстрактных представлений, мысленного отвлечения от многих свойств и связей оригинала и выделения тех сторон и признаков, которые отражают сущность его и представляют важность для исследователя..

Порядок выполнения операций при построении физической модели следующий:

○ Исследование всех действующих факторов (переменных), определяющих поведение исследуемого объекта; разделение их на значащие (главные, определяющие), и незначащие (второстепен-ные). Констатация (формулировка) допущений по особенностям использования действующих в объекте связей (в том числе о линейности и нелинейности этих связей, статичности и динамичности его характеристик – постоянных и параметров);

○ Выбор способа математического описания связей элементов объекта, обоснование применимости его к изучаемым процессам;

○ Запись связей элементов объекта, сохраненных в физической модели, в математических символах, в виде блок схемы получения ответа по исходным данным, в виде программы для ЭВМ или в виде состояния памяти ЭВМ (особенно по отношению к кибернетическим задачам).

На этом фактически заканчивается математическое моделирование. В выше приведенных процедурах основная работа ложиться на специалистов, владеющих предметом исследования.

Использование математической модели возможно только после исследования полученной физической модели и системы уравнений или алгоритмов на корректность формулировки ее по отношению к объекту, физическим и другим законам природы, на существование и единственность решения, на устойчивость и другие косвенные характеристики.

На этом этапе необходима совместная работа составителей и математиков, способных выбрать математический аппарат (или скорректировать его) и оценить возможность решения на базе сформулированной задачи. Возможность решения задач без предварительного математического исследования возникает при выполнении основного требования ко всем операциям на этапе моделирования, определяющим адекватность (соответствие) ММ реальному объекту относительно выбранной системы характеристик.

Под этим обычно понимается:

○ правильное качественное описание объекта по выбранным характеристикам, способное воспроизвести все изменения его под действием определенных вынуждающих факторов (входных переменных);

○ правильное количественное описание объекта по выбранным характеристикам с разумной степенью точности.

Адекватность модели определяется не только исследуемым объектом и его моделью, но и видом рассмотренных в модели воздействий, выбранных классом откликов, а также принятым уровнем точности.

Даже в технике, где математика давно завоевала исследовательские позиции, ММ может оказаться из-за сложности какого-либо объекта неадекватной. Выявление с помощью таких моделей качественных характеристик изменения состояний реальных объектов помогает исследователю ориентироваться в сложных системах и изыскивать пути их совершенствования. Абсолютной адекватности не существует, так как невозможно полное тождество ММ и моделируемого объекта.

Оценка адекватности ММ обычно производится точностью совпадения значения выходных величин модели и реального объекта, в качестве которой выступают относительные погрешности модели по каждой переменной 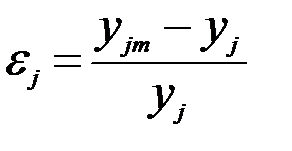, где y_im - выходная переменная, рассчитанная на модели; y_i – та же переменная объекта.

Точность модели по всему набору переменных (m) представляется среднеквадратичной величиной их точностей 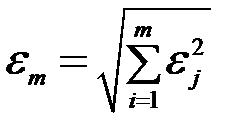или областью адекватности с указанием предельных значений точности по каждой из них.

Устанавливаемые предельные значения точностей по выходным данным определяют степень сложности математической модели по количеству значимых факторов уравнений, по длине алгоритмов счета, затратам машинного времени, требованиям к объему памяти ЭВМ. С другой стороны, соответствие модели реальному объекту зависит от степени изученности связей элементов, их составляющих. Успешное использование результатов анализа математической модели или синтеза сложного объекта будет зависеть от надежности описания этих связей.

При составлении математических моделей исследователь должен компромиссно разрешать противоречия между требуемой точностью и ограниченной сложностью модели.

В зависимости от задач исследования реальная система, являющаяся объектом, разными исследователями может быть описана различными математическими моделями, ни одну из которых нельзя отвергать, но можно все их ранжировать (расположить) по степени адекватности описания реального объекта в области эксплуатации, представляющей интерес в исследуемой задаче.

Адекватность модели часто нельзя строго оценить, и поэтому выбор для использования конкретной модели в значительной мере субъективен. Более простая модель может оказаться более точной в каком-либо диапазоне изменения входных переменных.

2. Разработка математического алгоритма, т.е. системы правил, задающей строгую последовательность математических операций, приводящих к искомому результату. Фактически этот алгоритм - совокупность цепочек алгебраических формул и логических правил, позволяющих установить нужную последовательность использования этих формул.

Расчетные формулы группируются по многократно повторяющимся циклам. Циклы образуют сложную структуру, включающую внутренние циклы, внешние и промежуточные. Структура в зависимости от полученных результатов может перестраиваться.

Для одной и той же задачи можно составить несколько алгоритмов, из которых надо выбрать по каким-либо критериям наиболее подходящий. Вопрос оценки алгоритма является предметом теории численных методов расчета, обязанной своим возникновением появлению на вооружении ученых ЭВМ. Цель теории численных методов - построение эффективных способов вычисления, которые позволяют получить решение задачи с заданной точностью при минимальном количестве действий с минимальной затратой машинного времени.

Коротко требования к математическому алгоритму могут быть сформулированы следующим образом:

o Удобство для машинного счета;

o Универсальность алгоритмов, пригодность для широкого класса типичных задач;

o Выделение задач, которые являются составной частью многих математических моделей, с разработкой для них эффективных алгоритмов в виде стандартных (прикладных) программ для ЭВМ.

3. Создание программы для реализации вычислительного алгоритма на ЭВМ (машинного алгоритма). В настоящее время программирование (перевод вычислительных алгоритмов в машинные) осуществляется с помощью машинных языков, облегчающих общение с машиной. Машинный язык выбирается исходя из класса задач, которые предстоит решить.

4. Проведение расчетов на машине. На этом этапе проявляется сходство расчетов с натурным экспериментом, поэтому часто он называется вычислительным экспериментом. В лаборатории ученый ставит вопросы природному явлению, промышленной установке, специально созданной экспериментальной установке, а при работе на ЭВМ - математической модели. Как в натурном эксперименте, так и в вычислительном результат получается в виде цифрового материала, подлежащего обработке. Достоверность полученной машинным счетом информации определяется адекватностью модели объекту, поэтому вычислительный эксперимент в полном объеме не проводится сразу после написания программы. Сначала программа проверяется тестовыми расчетами по известным экспериментальным данным. Проводится отладка программы. Только после этой кропотливой работы начинается исследовательская работа по модели.

5. Обработка результатов, всесторонний их анализ и формулирование выводов.Если не требуется уточнения модели, то результаты обрабатываются в виде, нужном заказчику или постановщику задачи. При появлении в результатах счета необычных форм протекания процесса, неожиданных режимов работы исследуемой на модели установки проводится уточнение деталей процесса. Как правило, при этом модель усложняется, а исследование повторяется с первого этапа полностью.

Полученные данные (после окончательной отладки модели) представляют собой числовой массив, который должен быть каким-либо способом сгруппирован для проведения сущностного или поведенческого анализа исследуемого объекта (об этом частично будет сказано ниже). Способ объединения или классификации расчетных данных определяется задачей исследования, но во многих случаях он опирается на возможность получения ответа на следующие вопросы:

• общая апробация приемлемости исследования в целом;

• отыскание ответов на неожиданные аспекты исследования, которые, может быть, не связаны с поставленными ранее задачами в исследовании;

• представительное и экономное формулирование результатов, нацеленное на непосредственное практическое использование (оптимизация объекта, изменение структуры его на основании осмысливания ММ).

С первым пунктом связана верификация ММ на основе имеющихся опытных данных, со вторым – возможность формулировки новых направлений научных изысканий в отрасли, а с третьим - решение повседневных задач хозяйственной жизни предприятий, отрасли, всей страны или даже общечеловеческих задач.