Состояние объекта - это качественная его характеристика в заданный момент времени, оцениваемая определенными количествен-ными значениями набора некоторых его свойств.
В общем случае оценки характеристик, определяющих состояние объекта, являются какими-либо выходными переменными факторами, под которыми понимаются его «потребительские» свойства.
Примеров известных нам всем математических моделей можно привести много. Вот некоторые из них: математическая запись второго закона механики, закон Кирхгофа, закон Ома, закон, описывающий состояние идеального газа – характеристическое уравнение Клайперона
pv=RT,
где R тоже характеристика газа (газовая постоянная), и многие другие.
Свойства объекта в целом «измеряются» уровнем входящих в подобные ММ отдельных характеристик, изменение которых и свидетельствует об изменении состояния.
В наиболее знакомой нам области науки (теплотехнике) такими характеристиками для объекта, каковым являются идеальный газ, будут давление р и удельный объем газа v, а такжеабсолютная температура газа T. Изменение хотя бы одной из них изменяет свойства объекта: сжатый газ способен совершать работу, нагретый в свободном состоянии – высушивать какое-нибудь сырье.
Все названные характеристики объекта – газа (и любого другого),
способные изменить его состояние, называются переменными (величинами). Категория переменных является составной частью операндов ММ. В них входят также параметры и константы,к которым относятся величины, учитывающие природные свойства объекта. В нашем примере к константам относится универсальная газовая постоянная, R  . Внутренние природные свойства объекта не всегда остаются постоянными: они могут меняться с изменением условий существования объекта и даже быть какой-то их функцией. Такие свойства называются параметрами.
. Внутренние природные свойства объекта не всегда остаются постоянными: они могут меняться с изменением условий существования объекта и даже быть какой-то их функцией. Такие свойства называются параметрами.
Переход из одного состояния в другое определяется условиями, в которых находится объект.
В общем случае объект может характеризоваться любым числом переменных. В зависимости от поставленных составителем математической модели целей используются или учитываются те из них, которые являются значащими.
В природе почти все процессы инерционны, т.е. происходят во времени, поэтому переход объекта из одного состояния в другое может быть описан системой обыкновенных дифференциальных уравнений вида:
 (2.1)
(2.1)
где х1,…,xn – переменные величины, характеризующие состояние объекта; Р - характеристики самого объекта (параметры и константы); F - характеристики условий, в которых производится изменение состояний.
Функциональные зависимости ψ1,ψ2,...,ψn представляют собой закономерности, связывающие отдельные состояния объекта между собой. В такой записи они выражают скорости изменения переменных при переходе объекта из одного состояния в другое. В общем случае эти зависимости являются частными видами отношений, которые могут устанавливаться между элементами математического множества (состояний).
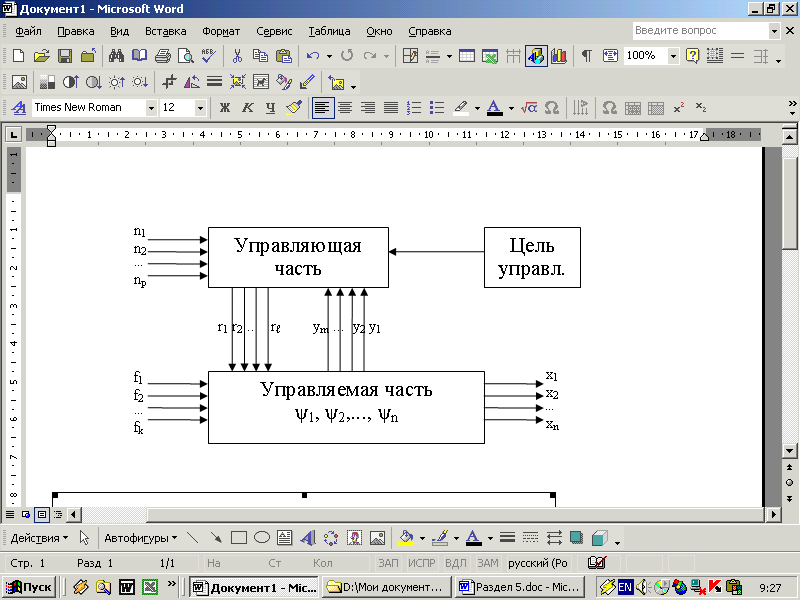
| Рисунок 2.1 Управляемая система |
|
Переменные, характеризующие состояние объекта, несут функциональную нагрузку, и с этой точки зрения они подразделяются:
· на выходные переменные x1(t), x2(t), …xn(t), отражающие основные стороны поведения системы [вектор Х (t)];
· переменные управления r1(t), r2(t), …rℓ(t), отражающие воздействия со стороны управляющей части (например, регулятора двигателя внутреннего сгорания - вектор R (t));
· возмущающие воздействия f1(t), f2(t), …fк(t), действующие со стороны внешней среды (вектор F (t));
· переменные воздействия на управляющее устройство n1(t), n2(t),... nр(t), являющиеся помехами в регулирующем устройстве или какой-то дополнительной информацией о возмущениях F, попадающей непосредственно в управляющее устройство (вектор N (t));
· наблюдаемые переменные y1(t), y2(t),...ym(t) - некоторые характеристики выходных переменных, определяемые целью регулирования (вектор У(t)).
Общий вид ММ управляемой системы включает три группы дифференциальных уравнений:
1) связи вектора переменных, включающих, кроме самих переменных, воздействия и их производные, Х0 (t),и таких же векторов управления и возмущающих воздействий ( R0 (t) , F0 (t);
2) связи вектора управления R0 (t) с векторами переменных воздействия N0 (t) и наблюдаемых переменных У0(t) при действующем законе управления g;
3) связи вектора наблюдаемых переменных У0(t) c выходными переменными (с результатом действия регулятора).
Математическая модель в самом общем случае представляется системой дифференциальных уравнений
Х(Х0)=Φ (R0,F0),
R(R0)=P(y0,N0,g), (2.2)
У0=cХ0.
Каждой ММ свойственна область существования. Она может быть непрерывной и дискретной. Непрерывная область характеризуется бесконечно малым изменением свойств объекта в бесконечно малой окрестности рассматриваемой точки. Дискретная – резким изменением в некоторых переходных точках (примеры: переход воды из твердого состояния в жидкое, а потом в парообразное; взрыв урановых материалов при достижении критической массы).
Качественные характеристики иногда плохо описываются количественно. Для перевода качественных характеристик (это обычно нечеткие оценки свойств объекта) в фиксированные количественные показатели используется кодирование их натуральными числами. Примеры таких шкал кодирования – шкала предпочтения Заде (таблица 2.1) и шкала Харрингтона (таблица 2.2).
Таблица 2.1 Шкала кодирования предпочтения Заде
| Численность оценки | Оценка | Пояснения |
| Отсутствие предпочтений | Два объекта дают равный вклад в цель | |
| Слабое предпочтение | Оценка слегка в пользу одного из объектов | |
| Сильное предпочтение | Оценка существенно в пользу одного из объектов | |
| Очень сильное предпочтение | Один объект сильно доминирует над другим | |
| Абсолютное предпочтение | Очевидна высшая степень предпочтения | |
| 2,4,6,8 | Промежуточные оценки | Необходим компромисс |
Таблица 2.2 Шкала желательности Харрингтона
| Желательность | Отметки на шкале |
| Очень хорошо | 1,00...0,80 |
| Хорошо | 0,80...0,63 |
| Удовлетворительно | 0,63...0,37 |
| Плохо | 0,37...0,20 |
Дата добавления: 2015-11-12; просмотров: 1246;
