Их классификация, свойства, области применения

Решение системы уравнений (ММ), помеченной вторым номером, позволяет тем или иным способом получить вектор состояния Х(t), зависящий от времени. Его значения, отнесённые к прошлому, будут историей переходов, а к будущему – предсказанием его поведения. По существу он выражает эволюцию развития состояний.

В задаче, решённой таким образом, обязательно все процессы, явления настолько детерминированы, что функционирование объекта никоим образом внезапными изменениями не может быть нарушено.

Однако не всегда наблюдаются именно такие объекты. Некоторые объекты в некоторых прошлых промежутках времени были определены, получен набор состояний по времени, но физические (функциональные) отношения перехода состояний не установлены, проще сказать закономерности такого перехода неизвестны.

В этом случае задача прогнозирования поведения объекта не может быть решена с большой надёжностью осуществления.

Общим способом решения математического моделирования таких объектов является идентификация прошлых состояний – экспериментальное установление вида интегральной зависимости вектора состояний от вектора входных воздействий по известному прошлому с последующей экстраполяцией (распространением на будущее) этой функции.

Задача идентификации записывается э таком виде:

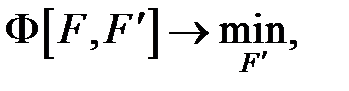
где F - неизвестный оператор (функция), описывающий объект во времени; F' - аппроксимация оператора F.

На самом деле идентификацию по приведенному выражению провести нельзя (F – не известен), поэтому идентичность ему аппроксимации F' оценивается идентичностью выходов модели F' и действительного объекта:

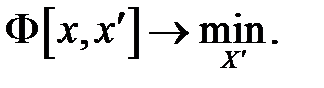
Проще всего идентификация осуществляется для объектов, для которых вид аналитической функции F' известен (например, сила тока в цепи переменного тока описывается законом косинусов, поэтому определить при идентификации надо только его амплитуду). Такой вид идентификации носит название параметрической. Определение характеристик функции в этом случае осуществляется методами линейной аппроксимации, наименьших квадратов. Раздел науки, который занимается этим, называется адаптацией и обучением в автоматических системах или адекватной идентификацией.

Системы и задачи, в которых это можно сделать, называются системами с устранимой информативной неопределенностью (за счет увеличения опытных данных). Обычно они характеризуются большим набором переменных, влияющих друг на друга, но подчиняющихся некоторым усредненным закономерностям. Иногда, правда, это достигается за счет структурной адаптации, состоящей в подборе аппроксимационной функции в виде разложения по некоторой системе известных функций:

(2.3)

где вектор β=(β₁, β₂,…β_n) определяется в ходе параметрической адаптации.

Соотношение (2.3) может быть еще и функцией параметра α, поэтому идентификация осуществляется по α и β.

В более сложных системах обязательно возникают случаи неустранимой информационной неопределенности в свойствах и характеристиках состояния объекта.. Никакое увеличение объема экспериментальной информации не устраняет информативной неопределенности, и всякая составленная для таких объектов математическая модель не будет соответствовать ему в ближайшее время.

Управление такими сложными системами можно производитьтолько с помощью алгоритмов самоорганизации, обеспечивающих возможностьперехода одного класса модели к другому по структуре и функционированию.

Способы создания алгоритмов самоорганизации – это предмет

изучения науки, которая называется кибернетикой. Кибернетика сформулировала свойства алгоритмов самоорганизации. Их четыре:

○ постоянное взаимодействие с объектом для непрерывного получения информации;

○ обязательное наличие стохастической (вероятностной) части;

○ значительная структурная и функциональная избыточность;

○ иерархия (многоуровневая связь) организации и многообразие задач, решаемых на различных уровнях.

В таких условиях в качестве цели бессмысленно ставить вопрос достижения выработки оптимальных управляющих воздействий, а можно говорить лишь об удовлетворительных решениях. Сама идея такой рационализации носит все-таки название принципа оптимальности Беллмана, который гласит: оптимальная стратегия характеризуется той особенностью, что, какими бы ни были начальное состояние системы и последствия ранее принятых относительно нее решений, все дальнейшие действия должны составлять оптимальную стратегию, исходящую из состояния системы, явившегося результатом прежних решений.

Самоорганизующиеся алгоритмы необычайно сложны в реализации. Не случайно распространение получили пока алгоритмы самонастройки, являющиеся подклассом самоорганизующихся алгоритмов. При самонастройке изменяются лишь некоторые параметры алгоритма, цель которого поддержать на заданном уровне определенные характеристики объекта.

При этом сложные модели приходится разделять на более простые элементы (т.е. использовать принцип декомпозиции) и рассматривать их как структурные модели с определенными характеристиками: функциональными (набором операторов) и структурными (графом взаимосвязи).

Набор операторов – это некие заготовки, а структура – каркас модели, соединяющий каким- либо входы и выходы модели. Этим самым моделирование объекта заменяется моделированием его эволюции (смены каркасов). Принцип такого моделирования называется принципом искусственной эволюции Л. Фогеля. Демонстрируется он элементами самых простых предсказывающих и распознающих алгоритмов. В этих алгоритмах и возникает необходимость иерархии программируемых действий: нижний уровень в режиме реального времени используется для предсказания «поведения» объекта при постоянном наборе структурных моделей, а верхний – за счет «мутаций» (внезапных изменений) структур каркасов путем случайного поиска как самоорганизуюшийся алгоритм готовит новые структуры. При «сбоях» модели во время счета эти вновь формирующиеся структуры должны обеспечить замену старых связей в алгоритме новыми.

МЕТОДЫ ПОСТРОЕНИЯ