ОСНОВИ РЕГРЕСІЙНОГО АНАЛІЗУ

3.1 Поняття про регресійний аналіз.

Основне завдання регресійного аналізу це встановлення форми і виявлення залежностей і змін.

Одне з головних завдань регресійного аналізу полягає у підборі відповідного виразу Y=f(X) , графік якого проходить через емпіричні точки або близько від них. І таким чином зв’язані змінні Х та Y. Даний вираз має назву рівняння регресії, функція f(X) називається функцією регресії. Графік даної функції називається лінією даної регресії. Тобто регресійний аналіз виявляє кількісну залежність ознаки фактора від іншої ознаки. В загальному випадку побудова лінії регресії починається з візуального аналізу розкиду даних вхідних змінних. Крім того часто будують так звану емпіричну лінію регресії. При цьому весь діапазон зміни Х розбивається на S рівних інтервалів ∆Х. Всі точки які попадають на інтервал ∆Х відносять до його середини. Після чого підраховують так звані ковзні мат. Очікування:

.

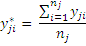Емпірична лінія регресії y від x одержується у вигляді ламаної лінії шляхом послідовного з’єднання відрізками ліній точок.

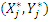
Після встановлення форми залежності, якщо вона явно є не лінійною, здійснюють перетворення системи координат таким чином щоб дану нелінійність лінеаризувати. Для детальнішого ознайомлення рекомендується звертатись до спеціальної літератури.

Параметри або коефіцієнти емпіричних моделей можуть встановлюватись методом найменших квадратів і методом максимуму правдоподібності.

Типова і основна задача ставиться наступним чином:

Необхідно встановити параметри а₀ і а₁ для залежності

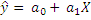
на вибірці об`єму n.

У методі найменших квадратів дані параметри визначаються з умови мінімуму наступного критерію

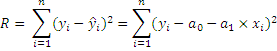
на основі чого було оодержано наступні формули:

,

.

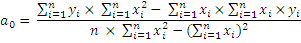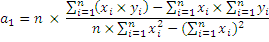У методі максимальної правдоподібності апроксимуюча залежність розглядається як функція математичного очікування випадкової величини від невипадкового аргумента. При цьому метод передбачає що випадкова величина відповідає нормальному закону розподілу. Такий підхід приводить до мінімізації наступного критерію:

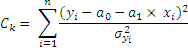
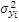– це оцінка дисперсії в даній точці.

Множинна регресія – це оцінювання наприклад, змінної Y лінійною комбінацією mнезалежних змінних X1, X2, Xm. Найпростіший варіант регресії має місці для m=2, коли необхідно спрогнозувати залежність однієї змінної Y від двох змінних X1 та X2. Рівняння множинної регресії має вигляд:

,

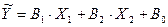де: , , ;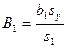

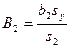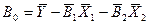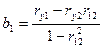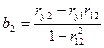, . У наведених виразах:

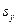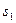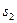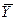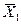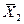, , , , , – cтандартні відхилення та середні значення Y, X1 та X2;

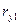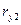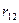, , – коефіцієнти кореляції Пірсона між Y i X1, Y і X2, X1 і X2.