Використання кореляційно–регресійного аналізу
При визначенні конкретних залежностей одні показники розглядаються як фактори впливу (ознаки), щ обумовлюють зміни іншого показника (результативного фактора). Функціональні зв'язки характеризуються повною відповідністю між змінами факторної ознаки змінами результативної величини, причому кожному значенню фактора-ознаки відповідає певне значення результативного фактора. При кореляційних зв'язках між змінами факторів-ознак та результативного показник повної відповідності не існує.
Вплив окремих факторі виявляється лише в середньому при значній кількості спостережень фактичних даних. Крім того, фактор - ознака, як правило, залежить від зміни інших показників.
Форма взаємозв'язку випадкових величин і функції дістала назву рівняння регресії. Виділяють парну (просту) та множинну регресії лінійного і нелінійного (квадратичного, експоненціального, напівлогарифмічного типів. Вид, а також параметри рівняння регресії знаходять за допомогою методу найменших квадратів. За наявності кореляційної залежності визначають лише тенденцію зміни результативного показника при зміна факторів-ознак.
Найчастіше застосовуються такі математичні залежності для оцінювання кореляційного зв'язку між факторами:
• прямолінійна
у = а0 +а1х, де а0 — стала (область існування моделі); а, — коефіцієнт регресії, що характеризує середню зміну результативного показника при змінах фактора-ознаки;
• параболічна
у = а0+а1х +а2х2
• показникова
у = а0+а1х
• степенева
y=a0ха1,
• гіперболічна
у=а0+ 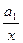
• напівлогарифмічна
у =а0+а1lgx
Статистичне оцінювання тісноти зв'язку грунтується на показниках варіації:
• загальній дисперсії sу2 результативного показника, обумовленій впливом усіх факторів у сукупності;
• факторній дисперсії sух2 результативного показника, що показує його варіацію під впливом окремих факторів;
• залишковій дисперсії sS2 результативного показника, яка показує його варіацію під впливом усіх факторів, крім виділеного, причому
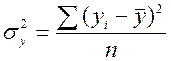
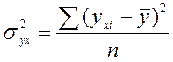
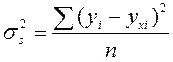

Якісною оцінкою ступеня зв'язку випадкових величин виступає коефіцієнт детермінації, що визначається виразом R2 = 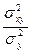 відношенням факторної та загальної дисперсій. Індекс кореляції розраховується як квадратний корінь із коефіцієнта детермінації, тобто
відношенням факторної та загальної дисперсій. Індекс кореляції розраховується як квадратний корінь із коефіцієнта детермінації, тобто
R =  , причому його значення лежать у межах від –1 до +1 (знак «мінус» указує на наявність зворотного зв'язку між факторами).
, причому його значення лежать у межах від –1 до +1 (знак «мінус» указує на наявність зворотного зв'язку між факторами).
Для оцінювання значущості індексу кореляції можна використовувати F'-критерій Фішера.
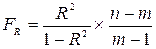
де п — число значень у масиві; т — число параметрів рівняння регресії (факторів). Фактичне значення цього критерію порівнюють із критичним значенням, яке визначають з урахуванням рівня значущості та кількості ступенів вільності. Якщо фактичне значення -F-критерію Фішера більше від критичного, то індекс кореляції R вважається істотним.
Дата добавления: 2015-09-11; просмотров: 1115;
