Середні величини та їх обчислення засобами табличного процесора MS Excel

Наступними узагальнюючими показниками після абсолютних і відносних величин є середні величини і показники варіації.

Середньою величиною у статистиці називається узагальнююча характеристика сукупності однотипних явищ з будь-якої варіаційної ознаки, що показує рівень ознаки, розрахований на одиницю сукуп­ності. Разом із методом групувань середні величини у статистиці є одним з основних методів опрацювання й аналізу масових даних.

Значення середніх величин у тому, що вони:

• допомагають в аналізі, даючи змогу кількісно охарактеризувати найважливіші закономірності суспільного життя, що проявля­ються у зростанні середньої продуктивності праці, зниженні се­реднього рівня злочинності, середніх витрат сировини та матері­алів, електроенергії та ін.;

• широко застосовуються у практиці планування виробничо-госпо­дарської діяльності підприємств, фірм, банків та інших госпо­дарських одиниць. Планові завдання складаються на основі се­редніх норм виробітку, витрат сировини, матеріалів, електро­енергії тощо;

• необхідні для вивчення взаємозв'язків між досліджуваними озна­ками та діючими на них факторами. У правовій статистиці середні величини використовуються для обчислення середнього терміну розгляду справ, середньої кількості справ на одного працівника суду, середньої чисельності осіб, що при­падають на одну кримінальну справу, середнього віку засуджених. За допомогою середніх величин можна порівняти судову практику призначення карних покарань у двох районах (областях), схожих за рів­нем і структурою злочинності. Середня величина як категорія стати­стики — це, з одного боку, реальний показник, що відображає об'єк­тивно існуючі властивості суспільних явищ (так, безумовно, існують строки покарання за злочини, терміни розгляду окремих справ дея­кими суддями), на основі яких можуть бути обчислені середні показ­ники; а з другого — у ній взаємознищуються індивідуальні розхо­дження багатьох величин одного і того самого виду. Середня величи­на абстрагується від індивідуальних розходжень ознаки, але зберігає їхні основні властивості, загальні умови. Філософський зміст се­редніх величин обгрунтував А. Кетле. Згідно з вченням А. Кетле, масові процеси і явища формуються під впливом двох груп причин:

• які визначають стан масового процесу, вони загальні для всіх одиниць сукупності;

• випадкових, тобто таких, що формують специфічні особливості

окремих одиниць сукупності, а отже, і відхилення від типового

рівня.

При обчисленні середніх величин для великого числа одиниць су­купності випадкові причини взаємознищуються, і середня, абстрагу­ючись від індивідуальних особливостей окремих одиниць, виражає загальні властивості, притаманні всім одиницям сукупності.

Середні величини дають правильну характеристику сукупності суспільних явищ, якщо дотримуються такі умови їх застосування:

1. Середні величини повинні обчислюватися тільки для якісно од­норідних сукупностей стосовно досліджуваної ознаки. Якісна од­норідність сукупності визначається попереднім економічним аналізом.

2. Метод середніх величин потрібно поєднувати з методом групу­вань. Неоднорідну сукупність необхідно розбити на однорідні групи. Замість загальної середньої величини, треба обчислити середні для однорідних груп.

3. Середні для об'єктивнішого аналізу необхідно доповнювати ін­дивідуальними значеннями ознак, тому що середня гасить будь-які індивідуальні відхилення. За благополучними середніми прихову­ються хиби на окремих ділянках роботи або якісь досягнення.

4. Середні величини мають обчислюватися не на основі поодино­ких фактів, а масових суспільних явищ відповідно до закону великих чисел. Тоді взаємознищуються можливі випадкові відхилення і серед­ня величина правильно характеризує типовий розмір ознаки.

5. Необхідно знайти правильний спосіб обчислення середньої ве­личини. Статистика використовує багато видів середніх величин. Але правильну характеристику сукупності з варіюючої ознаки дає тільки один вид середньої величини.

Середня арифметична величина.Найпоширенішим видом середньої є середня арифметична. Вона обчислюється, коли є дані про окремі значення ознаки, що варіює, і про число всіх одиниць сукупності, щодо якої визначається середнє значення цієї ознаки.

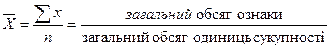
Розрахунок проведений за середньою арифметичною простою. Вона застосовується, коли дані не згруповані або частоти однакові, у випадку неоднакових частот формула має вигляд (так звана середня арифметична зважена):

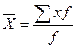
Середня геометрична величина.Для вивчення інтенсивності розвитку яких-небудь явищ у часі ви­користовується середня геометрична величина.

Якщо розрахунок проводиться на базі рівнів ряду динаміки, то застосовується формула

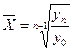
де X — середній темп росту; у_n — останній рівень ряду динаміки; у₀ — базисний рівень ряду динаміки (часто перший); п — число років (пе­ріодів).

Якщо відомі темпи динаміки за кожний рік, то розраховується се­редній темп зростання за весь період за формулою

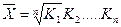
де К₁....К_n – ланцюгові темпи динаміки, n – кількість ланцюгових темпів динаміки.

Мода і медіана. Модою у правовій статистиці називають значення ознаки (варіан­та), яка найчастіше зустрічається в досліджуваній сукупності (Мо).

У дискретному ряду розподілу модою буде варіанта, що має най­більшу частоту.

Медіаною у правовій статистиці називається варіанта, що розта­шована в середині рангованого ряду і поділяє його навпіл (Me).

Щоб визначити медіану в дискретному ряду, потрібно суму час­тот ділити на 2 і до отриманого результату додати 0,5. Так визнача­ють номер, під яким стоїть медіана в ранжованому ряду.

На відміну від середніх, що е своєрідною статистичною абстрак­цією, мода і медіана — величини конкретні. На практиці іноді вико­ристовують моду замість середньої арифметичної або разом із нею.

Показники варіації.Середні величини дають узагальнену характеристику варіюючої ознаки досліджуваної сукупності. Розрахувавши їх, необхідно усвідо­мити, наскільки вони типові, надійні та наскільки однорідна су­купність за досліджуваною ознакою.

Статистичні сукупності можуть мати однакові значення серед­ньої, але значно відрізнятися коливаннями індивідуальних даних. За характером і ступенем відхилення (варіації) ознаки можна зробити висновок щодо якісної однорідності статистичної сукупності та на­дійності самої середньої.

Таким чином, середні величини рівні, а ряди істотно різняться між собою: перший ряд однорідніший, а отже, і середня надійніша, ніж у другому ряду.