Поняття про моделі та моделювання

Метод моделювання є одним з основних методів пізнання закономірностей усіляких процесів і явищ. У природних і прикладних науках найбільш розповсюдженим є фізичне і математичне моделювання.

Фізичне моделювання засноване на створенні деякого макета досліджуваного явища і дає значний економічний і тимчасовий ефект. Однак, фізичне моделювання має обмежену сферу застосування, особливо для складних систем.

Більш розповсюдженим є метод математичного моделювання, що бурхливо розвивається в останні десятиліття в зв'язку з появою нових обчислювальних засобів.

Математична модель являє собою систему математичних формул, з більшою чи меншою точністю, що описує процеси, що проходять у досліджуваній системі. При цьому дуже часто різні явища можуть мати однакову математичну модель.

Однак при рішенні практичних задач недостатньо мати математичну модель досліджуваної системи, необхідно також уміти використовувати її для прийняття рішень по оптимальному керуванню такою системою. Прикладом можуть служити методи селекції, засновані на математичній моделі популяционной генетики.

Сукупність математичних методів, які застосовують для обґрунтування рішень у всіх областях цілеспрямованої людської діяльності, прийнято поєднувати під загальною назвою "Дослідження операцій". Ця наука зобов'язана своєю появою і розвитком створенню й удосконалюванню ЕОМ.

Операцією називають будь-яку цілеспрямовану і керовану дію.

На першому етапі дослідження операції необхідно скласти її математичну модель. Загальних методів побудови математичних моделей не існує, але можна виділити наступні основні стадії побудови математичної моделі операції:

1. Створення функціональної (наочної, описової) моделі, тобто формування основних законів, які зв’язують об'єкти, що моделюють явища. При цьому реальне явище спрощується, схематизується. Функціональна модель повинна відбивати основні риси явища виходячи з цільової спрямованості операції.

2. Вибираються параметри моделі, які можна розбити на три групи:

а) задані, заздалегідь відомі фактори (умови, обмеження) a₁, a₂,…,a_k, на який ми впливати не можемо;

б) невідомі (випадкові) фактори b₁, b₂,…,b_l, значення яких не можна пророчити заздалегідь;

в) залежні від нас фактори (елементи рішення) x₁, x₂,…,x_n, які ми у відомих межах можемо вибирати за своїм розсудом.

3. Складають систему обмежень і зв'язків між параметрами у виді рівнянь, нерівностей і т.д., що адекватно відбиває закони і зв'язки функціональної моделі:
Ф_i(a₁, a₂,…,a_k,b₁,b₂,…,b_l,x₁,x₂,…,x_n)=0, 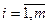чи Ф_i(x₁, x ₂,…,x_n)=0, ...
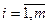Усякий визначений вибір залежних від нас параметрів і якийзадовольняє даній системі обмежень називають припустимим рішенням (планом). Множину усіх припустимих у даній операції рішень називають областю припустимих рішень (ОДР = G).

4. Для вибору рішення, що найбільше ефективно реалізує мету операції, необхіден кількісний критерій, що називають показником ефективності операції. На цій стадії складають цільову функцію залежності показника ефективності від параметрів моделі, оптимальне (максимальне чи мінімальне) значення якої необхідно знайти: F = F(a₁, a₂,…,a_k,b₁,b₂,…,b_l,x₁,x₂,…,x_n) чи F = F(x₁, x ₂,…,x_n)...

Якщо ОДР містить кінцеве число рішень, то знайти оптимальне значення цільової функції можна звичайним перебором, підставивши всі можливі рішення в цільову функцію і вибравши найбільше чи найменше значення F. Якщо ж число можливих рішень дуже велике чи нескінченно, то для пошуку оптимального рішення застосовують спеціальні методи цілеспрямованого перебору, розроблені зокрема в спеціальному розділі математики – "Математичне програмування".

У загальному випадку задачу математичного програмування можна поставити в такий спосіб. Знайти найбільше (найменше) значення цільової функції:

F(x₁, x ₂,…,x_n)®max(min) (1)

на припустимій множині G, де G задається системою обмежень у виді нерівностей і (або) рівностей:

g_i(x₁, x ₂,…,x_n)=(<,>,£,³,¹)0, де 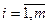. (2)

Якщо всі функції F і g_i – лінійні, то задачу (1) – (2) називають задачею лінійного програмування, у противному випадку говорять про нелінійне програмування. Якщо область G складається з окремих ізольованих точок, то говорять про дискретне або целочисельне програмування. Дослідженням багатокрокових операцій займається динамічне програмування.

Усі вищезгадані задачі математичного програмування відносять до так називаних детермінованих моделей, тобто, які не утримують невідомих параметрів b₁, b₂,…,b_l... При наявності таких параметрів говорять про вибір в умовах невизначеності. У кращому випадку параметри b₁, b₂,…,b_l являють собою випадкові величини з відомими законами розподілу імовірностей. Такі задачі вирішує стохастическое програмування. Набагато гірше випадок, при якому розподіл цих параметрів невідомий або взагалі не існує (методи гарантованого виграшу, експертних оцінок, алгоритмів, що адаптуються). Випадками ворожої невизначеності, коли в операції бере участь дві чи більш сторони з протилежними інтересами, займається спеціальний розділ математики – "Теорія ігор".

Усі перераховані методи досліджують операції з одним критерієм оптимальності. Задачі з декількома критеріями набагато складніше і, крім того, принципово не можуть мати чисто математичного рішення (задача одержання найбільшого прибутку з найменшими витратами). Математичні методи дослідження операцій у багатокритериальных задачах дозволяють лише виділити оптимальну множину рішень, що свідомо краще інших. Остаточний вибір залишається суб'єктивним.