Розрахунок параметрів лінії регресії.
Етап 2. Будуємо рівняння множинної регресії та оцінюємо одержані результати. Для виконання цього етапу можна використати інструментРегрессия або статистичні функції.
Для роботи з інструментомРегрессия вхідні дані треба розмістити з дотриманням таких вимог:
• масиви даних розміщуються у стовпцях;
• перший рядок — назви показників;
• перший стовпець даних — масив у (результативний фактор), інші нерозірвані масиви х — масиви факторів-ознак.
Лінійний регресійний аналіз полягає у виборі графіка для відображення спостережень за допомогою методу найменших квадратів. Регресія використовується для аналізу впливу на залежну змінну значень однієї або більше незалежних змінних-факторів.
Параметрами діалогового вікнаРегрессия є (рис. 124):
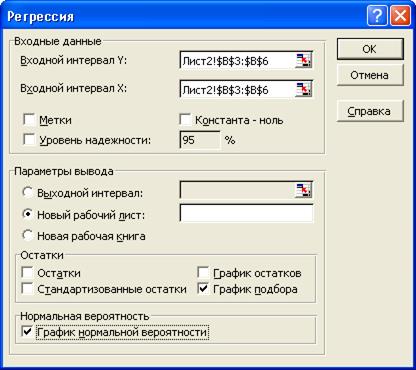
Рис. 124. Діалогове вікно команди Регрессия.
• вхідний інтервал Y — посилання на діапазон результативного показника. Діапазон має складатися з одного стовпця;
• вхідний інтервал Х — посилання на діапазон факторів-ознак. Максимальне число вхідних показників дорівнює 16;
• мітки — параметр для автоматичного формування назв показників;
• рівень надійності — дає змогу включити у вихідний діапазон рівень надійності до 95 %, що вводитьсяза замовчуванням;
• константа-нуль — прапорець, який вказує, що лінія регресії проходить через початок координат;
• вихідний діапазон — посилання на ліву верхню клітинку вихідного діапазону активного робочого листка, нового робочого листка або нової робочої книги. При цьому можна задати ім'я нового робочого листка, де вихідний діапазон почнеться з клітинки А1;
• залишки — дає змогу включити залишки у вихідний діапазон;
• стандартизовані залишки — дає можливість включити стандартизовані залишки у вихідний діапазон;
• графік залишків — діаграма залишків для кожної незалежної змінної;
• графік підбору — діаграма даних, що спостерігаються, а також прогнозованих значень для кожної незалежної змінної;
• графік нормальної імовірності — діаграма нормальної імовірності.
У результаті виконання зазначених команд автоматично буде побудовано таблиці регресійного аналізу (рис. 125):

Рис.125. Таблиці регресійного аналізу.
ТаблицяРегрессионная статистика включає так показники для оцінювання адекватності моделі:
• коефіцієнт детермінації R2;
• індекс кореляції R;
•значення коефіцієнта детермінації при збільшенні кількості спостережень (нормоване);
• стандартну помилку;
• кількість спостережень.
ТаблицяДисперсионньїй анализ має таку структуру
• df — кількість ступенів вільності (т; п-т-1; п-1);
• SS — дисперсія (факторна, залишкова, загальна);
• MS — дисперсія/кількість ступенів вільності;
• F — оцінка зв'язку між незалежними факторами залежною змінною;
• значимость F — рівень значущості, що відповідає визначеному F — чим він нижче, тим кращий зв'язок.
ТаблицяПараметри модели має таку структуру:
• коэффициенты— значення параметрів моделі а0 аj
• стандартная ошибка — стандартна помилка параметрів рівняння;
• t-статистика — коефіцієнт/стандартна помилка;
• Р-значение — значущість для t-статистики;
• межі довірчих інтервалів для коефіцієнтів рівняння регресії при різних рівнях значущості.
Остання таблиця включає прогнозовані значення у ізалишки.
Одержане рівняння залежності можна використовувати для прогнозних розрахунків. Підставивши у це рівняння нове значення х, можна одержати прогнозоване значення у.
Для розширеного аналізу можна також розраховувати такий показник, як коефіцієнт еластичності:
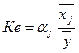
де aj— коефіцієнт у рівнянні залежності для j-го фактора; 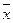 j— середньоарифметичне значення j-го фактора;
j— середньоарифметичне значення j-го фактора;
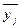 — середньоарифметичне значення результативного показника.
— середньоарифметичне значення результативного показника.
Коефіцієнт еластичності показує, на скільки відсотків у середньому змінюється результативний показник із зміною аргументу х на 1 %.
При проведенні кореляційно-регресійного аналізу можна застосовувати також додаткові статистичні функції для оцінювання параметрів моделі та залежності між факторами:
• НАКЛОН — визначає коефіцієнт a1 у рівнянні у = a0+ a1х;
• ОТРЕЗОК — визначає коефіцієнт a0 у рівнянні у = a0+ a1х ;
• ЛИНЕЙН — вводяться масиви у та х (можна декілька) — обчислюються коефіцієнти а1 і a0 або коефіцієнти у рівнянні з aj Вводити цю функцію у множинну регресію треба за правилами роботи з БД: виділити діапазон результатів (рядок із т + 1 клітинок); ввести функцію; введення формули закінчити одночасним натисненням на клавішіCtrl+Shift+Enter. Послідовність розміщення результатів відповідає параметрам моделі аm. am-1,... а1, a0;
• ПИРСОН — визначає коефіцієнт кореляції R у межах від -1 до +1;
• КВПІІРСОН — визначає коефіцієнт детермінації R2;
•СТОШУХ — визначає стандартну похибку прогнозних значень у для кожного значення х регресії;
•КОВАР — визначає коефіцієнти коваріації, а також середні попарні добутки відхилень.
Дата добавления: 2015-09-11; просмотров: 1219;
