Призначення дисперсного аналізу. Однофакторний аналіз.

Дисперсний аналіз – це статистичний метод аналізу результатів спостереження, що залежать від різних одночасно діючих факторів. Вибір найбільш важливих факторів та оцінка їх впливу. Ідея дисперсного аналізу полягає в розкладі загальної дисперсії випадкової величини на незалежні випадкові доданки. Кожний з яких характеризує вплив того чи іншого фактору або взаємодії факторів. Порівняння дисперсії дозволяє порівняти вплив факторів на досліджувану величину. Нехай наприклад Х – досліджувана величина, А і B – фактори, які впливають на досліджувану величину. Допустим що відхилення значень вибірки Х від середнього можна представити у вигляді:

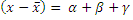
Де 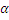відхилення визване фактором А, 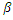– відхилення визване фактором В, 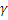– визване іншими факторами.

Крім того вважається що 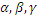незалежні випадкові величини.

Позначимо дисперсії величин Х 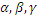відповідно через: 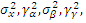. Тоді можна записати що:

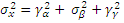
Порівнюючи сигма квадрат альфа і сигма квадрат бета з сигма квадрат гама можна встановити степінь впливу факторів А і В на величину Х у порівнянні з не врахованими факторами. Порівнюючи сигма альфа квадрат і сигма бета квадрат між собою роблять висновок про те який з факторів сильніше впливає на Х. Дисперсійний аналіз дозволяє на основі вибіркових даних визначити розглядувані значення а також використовуючи відповідні критерії оцінити суттєвість впливу фактору на досліджувану величину. Якщо досліджується вплив одного фактора на досліджувану величину то мова йде про однофакторний аналіз або однофакторна класифікація. Якщо вивчається вплив двох факторів то мова йде про двох факторний аналіз. При дисперсному аналізі визначається, що сукупності випадкових величин мають нормальний розподіл.

Суть математичних перетворень дисперсійного методу полягає в тому, щоб зіставити дисперсії за факторами із дисперсією усіх значень отриманих в експерименті. Однофакторний аналіз вимагає не менше трьох градацій фактора і не менше двох випробувань у кожній градації. При проведенні дисперсійного аналізу необхідно перевірити нормальність розподілу досліджуваної випадкової величини і відсутність відмінностей дисперсій сукупностей. Це можна виконати методами перевірки статистичних гіпотез.

Припустимо, що аналізується вплив фактора А на k рівнях А1, А2, …, Аk. Наприклад, в експерименті це можна реалізувати, якщо задіяти k вибірок з різними градаціями умов. На кожному рівні Аі (для кожної вибірки) проведено n спостережень 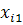, ,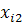…, 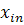(див.таблиця 1).

Розглянемо оцінки різних дисперсій.

Дисперсія 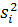для рівн 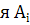(для певної вибірки) може бути записана як:

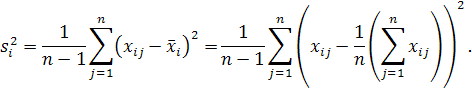
Таблиця 1 – Вихідні дані для дисперсного аналізу

Номери спостережень	Рівні фактора А
			…
			…
…	…	…	…	…
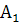
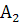
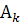
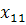
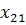
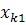
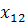
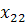
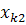
j			…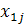
…	…	…	…	…
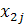
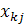
n			…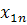
∑

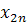
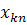
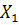
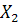
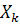
Дисперсія 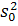, що характеризує варіативність поза впливом фактора А

.

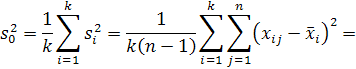
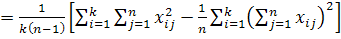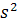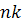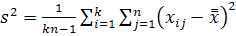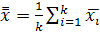Загальна дисперсія всіх спостережень дорівнює , де та 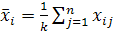. Отже,

.

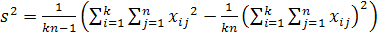Дисперсія 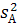, що характеризує зміну середніх 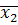під впливом фактора А:

.

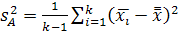Перевірка впливу фактора А на зміну середніх може бути зведена до порівняння дисперсій 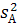та 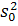. Вплив фактора А вважатиметься значущим на рівні α, якщо є значущим відношення 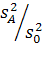, тобто, якщо:

,

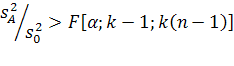де k-1; k(n-1) – ступені вільності F-розподілу, F – критерій Фішера.