Поняття про кореляційний аналіз.
Завданням описової статистики є не лише систематизація емпіричних даних чи оцінка типових параметрів вибірок і розподілів. Але й виявлення зв’язку між змінними. Оцінка їх напрямків та інтенсивностей. Кореляція – це статистична залежність між випадковими величинами що носить ймовірнісний характер. Кількісна міра кореляційного зв’язку найчастіше оцінюється значенням коефіцієнта кореляції від +1 до -1. Від’ємні значення кореляції свідчать про зворотній зв'язок додатній про прямий. Нульовою називається кореляція за відсутності зв’язку змінних.
Розглянем деякі методи пошуку кореляційних зв’язків.
Лінійна кореляція Пірсона дозволяє встановити лінійний кореляційний зв'язок:
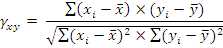
Коефіцієнти кореляції як міри зв’язку між випадковими величинами є також випадковими величинами і носять ймовірнісний характер. Статистичні висновки про кореляційний зв’язок між величинами роблять не з коефіцієнта кореляції одержаного із генеральної сукупності, а з його вибіркового аналогу. Отже статистика коефіцієнта кореляції потребує статистичної оцінки. Як правило перевіряє 0 гіпотезу про відсутність кореляційного зв’язку між змінними у генеральній сукупності. Достовірність коефіцієнтів кореляції залежить від прийнятого рівня значущості та обсягу вибірки. Статистика лінійного коефіцієнта кореляції Пірсона має такий вигляд:
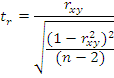 .
.
Нульову гіпотезу відхиляють на рівні значущості 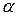 якщо критичне значення не перевищує емпіричного значення. Критичні значення для рівня значущості беруть за таблицями розподілу Стюдента.
якщо критичне значення не перевищує емпіричного значення. Критичні значення для рівня значущості беруть за таблицями розподілу Стюдента.
У тих випадках, коли одиниці досліджуваної сукупності можуть бути розміщені в певному порядку за зростаючими або спадаючими номерами або рангами в якості статистики зв’язку використовують рангові показники кореляції. Як правило ранг вказує місце яке займає дана одиниця серед інших одиниць. Якщо кожна з цих одиниць відрізнялась від всіх інших одиниць сукупності то ранги являли собою порядкові номери від одиниці до числа N рівного об’єму сукупності. Якщо деякі одиниці сукупності є однаковими то ранг всіх цих одиниць приймається середнім з їх відповідних номерів. Показних кореляції рівний:
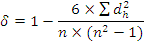 ,
,
де 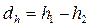 .
.
При вивченні складних явищ, як у нашому випадку, треба приймати до уваги більше двох величин. Правильне уявлення про природу зв’язків між цими величинами можна одержати лише в тому випадку, коли досліджені відразу всі розглядувані випадкові величини. Cпільне вивчення трьох (чи більше) випадкових величин може дозволити виділити вплив на одну з них іншої випадкової величини при деяких постійних значеннях решти величин. Таким чином статистичні розрахунки можуть підказати та обґрунтувати причинні залежності між досліджуваними явищами. Для вирішення таких завдань використовуються методи множинної та часткової кореляції.
Параметрами, які характеризують кореляцію між багатьма величинами, є множинні та часткові коефіцієнти кореляції. У випадку множинної кореляції параметри, що хаорактеризують стапінь зв’язку, э частковими випадками визначника кореляції 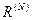 . Якщо вивчаються три взаємозв’язані величини
. Якщо вивчаються три взаємозв’язані величини 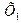 ,
, 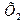 ,
, 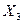 , коефіцієнт кореляції між
, коефіцієнт кореляції між 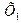 і
і 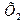
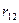 , коефіцієнт кореляції між
, коефіцієнт кореляції між 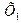 і
і 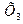
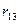 , коефіцієнт кореляції між
, коефіцієнт кореляції між 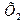 і
і 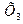
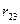 .
.
Із врахуванням того, що 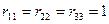 ,
, 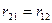 ,
, 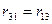 ,
, 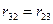 , визначник кореляції
, визначник кореляції 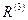 записують у наступному вигляді:
записують у наступному вигляді:
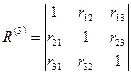
Мінори цього визначника рівні
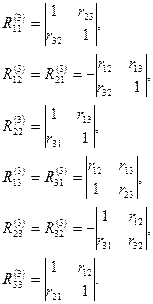
Множинний клефіцієнт кореляції 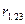 , як міра тісноти лінійного зв’язку випадкової величини
, як міра тісноти лінійного зв’язку випадкової величини 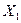 з двома іншими величинами визначається наступним чином:
з двома іншими величинами визначається наступним чином:
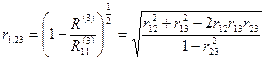 ,
,
У наведеній вище формулі перед коренем треба брати завжди знак плюс. Аналогічно визначаються решта співвідношень, за необхідності. Величина такого коефіцієнта кореляції завжди знаходиться в межах від 0 до +1.
Дата добавления: 2015-11-10; просмотров: 1411;
