Багатофакторний дисперсний аналіз.
Розглянем задачу оцінки дії одночасно двох факторів. Нехай наявні декілька типів однотипних станків і кілька видів сировини. Необхідно вияснити, на скільки суттєвим є вплив різних станків і якість сировини в різних партіях на якість одержуваної продукції. Дана задача є типовою задачею двох факторного дисперсійного аналізу. Нехай фактор А це вплив станків, фактор Bякості сировини з різних факторів, контрольний розмір оброблюваної деталі позначимо через Хij , для простоти зображення матриці спостережень розглянемо випадок коли для кожного станка і кожної партії сировини наявне лише одне спостереження, тоді матрицю спостережень можна записати у вигляді:
| Станки / Партії | b1 | b2 | … | bj | bv |
| A1 | X11 | X12 | X1v | ||
| A2 | X21 | X22 | X2v | ||
| …. | … | … | Xij | … | |
| …. | … | … | … | ||
| Ar | Xr1 | Xr2 | Xrv |
Тобто наявні F станків у матриці спостережень їм відповідають rрядків, які називаються рівнями фактора А, і є vпартії сировини в матриці їм відповідають vстовпців, які називатимемо рівнями фактора B. Перетин і-того рядка та j-того стовпця утворюють ijкомірку в яку записується спостереження (або спостереження у множині) при одночасному досліджені факторів А та Bдля кожного рівня відповідно. Для кожного стовпця і рядка обчислюється середнє значення а також загальне середнє для рядків можна записати наступним чином:
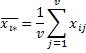 ,
,
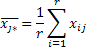 ,
,
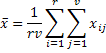 .
.
Основна тотожність дисперсного аналізу набуде вигляду:
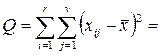
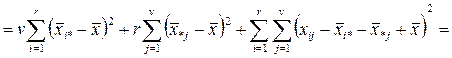
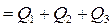
Тут :Q1 – це сума квадратів різниць між середніми по рядках і загальним середнім. Характеризує зміну ознаки по фактору А.
Q2 – характеризує зміну ознаки по фактору В.
Q3 – називається залишковою сумою квадратів характеризує вплив решти неврахованих факторів.
Вирази для відповідних дисперсій:
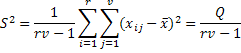
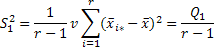
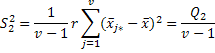
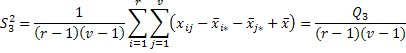 .
.
На основі Fкритерію обчислюється значимість наступних величин:
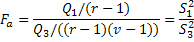 ,
,
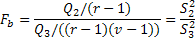 .
.
При одному спостереженні в комірці схема обчислень доволі проста, але достовірність висновків одежаних на основі такого підходу не достатня. Для вирішення практичних задач бажано мати кілька спостережень в одній комірці, в такому випадку обчислення ускладнюються проте висновки є більш достовіними.
Розглянемо схему двофокторного дисперсійного аналізу за наявності багатьох спостережень для кожної комірки. Пропорційним називається такий дисперсійний аналіз при якому кількість елементів в кожній комірці пропорційна або рівна.
Розглянемо двофакторний комплекс з рівним числом спостережень в кожній комірці. Матрицю спостережень наведемо нижче.
| B A | 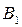
| 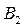
| . . . | 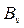
| 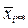
|
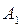
| 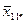
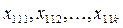
| 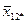
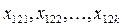
| . . . . . . | 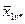
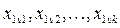
| 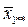
|
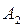
| 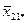
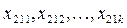
| 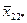
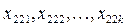
| . . . . . . | 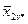
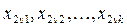
| 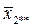
|
| . . . | . . . | . . . | 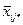
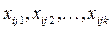
| . . . |
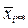
|
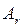
| 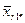
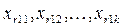
| 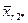
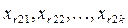
| . . . . . . | 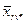
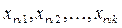
| 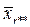
|
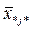
| 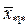
| 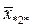
| . . . | 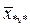
| 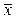
|
Тут:
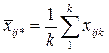 – середнє значення у комірці,
– середнє значення у комірці,
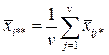 – середнє значення по рядку,
– середнє значення по рядку,
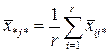 – середнє значення по стовпцю,
– середнє значення по стовпцю,
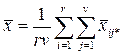 – загальне середнє;
– загальне середнє;
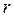 – число рівнів фактора
– число рівнів фактора 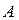 ,
,
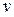 – число рівнів фактора
– число рівнів фактора 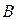 .
.
Схема аналізу наступна:
| Компонента дисперсій | Сума квадратів | Число ступеней вільності | Оцінка дисперсії |
| За фактором А | 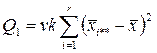
| 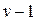
| 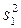
|
| За фактором B | 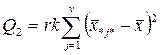
| 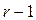
| 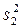
|
| Взаємодія | 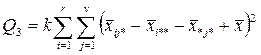
| 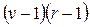
| 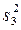
|
| Залишкова | 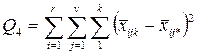
| 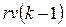
| 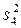
|
| Повна сума квадратів | 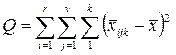
| 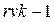
| 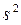
|
Сума 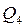 характеризує вплив інших випадкових факторів (крім факторів А, В, та їх взаємодії), тому для для встановлення значимості впливу факторів А і В величину дисперсії, обумовлену впливом цих факторів, порівнюють з дисперсією, обумовленою впливом інших факторів. При цьому обчислюють наступні співвідношення дисперсій:
характеризує вплив інших випадкових факторів (крім факторів А, В, та їх взаємодії), тому для для встановлення значимості впливу факторів А і В величину дисперсії, обумовлену впливом цих факторів, порівнюють з дисперсією, обумовленою впливом інших факторів. При цьому обчислюють наступні співвідношення дисперсій:
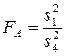 ,
, 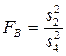 .
.
Обчислені значення порівнюють з табличними значеннями по критерію Фішера, які одержані для заданого рівня значущості та для відповідного числа ступеней вільності.
При більшій кількості факторів ідея розкладу дисперсій на складові залишається без змін, але схема аналізу стає доволі громіздкою. Загальна дисперсія розкладається на 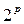 складових, де
складових, де 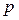 – порядок комплексу.
– порядок комплексу.
Методи дисперсійних досліджень за умови, що кількість даних різна у різних комірках, виходять за межі робочого плану, і їх рекомендується почерпнути у спеціальній літературі.
Дата добавления: 2015-11-10; просмотров: 910;
