Основи теорії оцінювання невідомих параметрів

При вивченні кількісних ознак, що характеризують сукупність однорідних обєктів не завжди є можливість досліджувати кожний обєкт сукупності.

Число обєктів генеральної сукупності або у вибірці називають обємом генеральної сукупності або вибірки. Задачу статистичного оцінювання параметрів можна сформулювати, як сукупність методів, які дозволяють робити науково обгрунтовані висновки про числові параметри генеральної сукупності на основі випадкових вибірок. Наприклад, якщо нас цікавить математичне оцінювання генеральної сукупності то задача статистичної оцінювання параметрів полягає у тому, щоб дати достовірне уявлення про параметр. Склад вибірки обмежений, тому висновки про достовірність такої оцінки не можуть бути 100% достовірні. Тому всякому рішенню, яке приймається при статистичній оцінці параметрів ставлять у відповідність ймовірність, яка характеризує степінь достовірності такого рішення.

Взагальному задача оцінки параметрів формулюється наступним чином. Позначемо через Х - випадкову величину, яка відповідає деякому закону розподілу F(X,Q) аналітичне представлення, якого відоме. Дана функція розподілу визначається деяким параметром Q чисельне значення якого є невідоме. Досліджувати всі елементи генеральної сукупності для обчислення параметру Q у більшості випадків неможливо, тому цей параметир оцінюютьна основі вибірок. Нехай здійснено m - вибірок тоді можна записати, що перша вибірка складається з елементів(x11,x12...x1n), друга вибірка(x21,x22 ...x2n). Позначемо вибірки як X1,X2,Xm. Всяку однозначну визначену функцію результатів спостережень над випадковою величиною X здопомогою, якої судять про значення параметра Q - називають оцінкою параметра Q.

В найзагалнішій формі можна записати, що 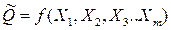оскільки X1, X2, Xm - випадкові величини то і Q випадкова величина. Найбільше практичне значення мають рівномірний розподіл та нормальний розподіл випадкових величин. Характеристики та параметри даних розподілів рекомендується повторити за курсом вищої математики.

Основними властивостями оцінок є властивість незміщеності, ефективності, та адекватності. Оцінка параметра називається незміщеною, якщо її математичне очікування рівне оцінюваному параметру. Незміщена оцінка, яка має найменшу дисперсію серед всіх можливих незміщених оцінок даного параметру, обчислених за вибірками одного й того самого обєму називається ефективною оцінкою.

Адекватність оцінки означає, що чим більший обєм вибірки тим більша ймовірність того, що ймовірність похибки оцінки буде не більша якогось наперед заданого малого числа.

У курсі теорії ймовірності та мат. статистики дається виведення двох таких теорем.

Теорема1: арифметичне середнє обчислене за n незалежних спостережень над випадковою величиною Х, яке має математичне очукування Mx є незміщеною та адекватною оцінкою.

Теорема 2: якщо випадкова вибірка складається з n незалежних спостережень з математичих очікування Mx та диперсією 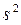то випадкова дисперсія не є незміщеною оцінкою генеральної сукупності.

.

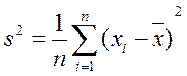Незміщена оцінка дисперсії генеральної сукупності визначається із співвідношення:

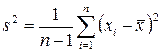
Для виводу, якщо n>50 різниця між зміщеною та незміщеною оцінками дисперсії вважається не суттєвою.