Поняття про варіаційний ряд та його характеристики
Генеральною сукупністю називають повну сукупність деякої ознаки або властивості. В більшості випадків робота з генеральною сукупністю не може бути здійснена через фізичну неможливість здійснення, або економічну недоцільність. Практично аналізується частина генеральної сукупності – вибірка. Вибіркою називають частину генеральної сукупності, одержану певним, як правило, науково обґрунтованим способом. Зрозуміло, що не всяка вибірка може представляти генеральну сукупність.
Для того, щоб за даними вибірки можна було достовірно судити про досліджувану ознаку генеральної сукупності, вибірка повинна бути репрезентативною. Вибірка є репрезентативною, якщо вона утворена випадковим чином. Існують різні способи відбору. В залежності від способі відбору розрізняють вибірки наступних типів:
– випадкова вибірка з поверненням;
– випадкова вибірка без повернення;
– механічна;
– типова;
– серійна.
Типовим способом, “історичним”, є спосіб одержання вибірки, при якому всім елементам генеральної сукупності присвоюється номер, який записується на листках паперу, що вкидуються у ящик. Після перемішування листки випадковим чином витягуються з ящика.
Перший спосіб – витягнута карточка після фіксації її номера повертається у пачку, після чого карточки знову перемішуються. Вибіркова сукупність, утворена за такою схемою, одержала назву випадкової вибірки з поверненням.
Другий спосіб – кожна витягнута карточка після запису її номера назад не повертається. Вибіркова сукупність, утворена по цьому принципу, називається вибірковою вибіркою без повернення.
При механічному способі утворення вибіркової сукупності елементи генеральної сукупності вибираються через певний інтервал. Даний метод дає задовільні результати за умови відсутності кореляції періоду відбору з будьякими виробничими періодами.
При великій кількості однорідної продукції, коли в її виготовленні беруть участь різні станки, цехи для утворення репрезентативної вибірки користуються типовим способом відбору. У цьому випадку генеральну сукупність попередньо розбивають на групи, що не пересікаються (по виробництву). Потім з кожної групи за схемою вибірки з поверненням або без повернення вибирають певне число елементів.
Серійний спосіб відбору полягає в тому, що генеральну сукупність розбивають на серії, які не пересікаються. З цих серій випадковим чином здійснюється кілька серій, на яких і здійснюється контроль з поверненням чи без повернення. Спосіб використовується для дуже великих виробництв і якщо якість виготовлення продукції на дуже високому рівні.
Для того щоб приступити до обчислення об’єму вибірки, необхідно задатись бажаною степінню точності ∆ і довірчою ймовірністю (1-α).
Для методу випадкової вибірки з поверненням використовується вираз:
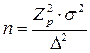 ,
,
де 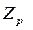 – табличне значення інтегралу ймовірності для нормального закону розподілу; обирається на основі
– табличне значення інтегралу ймовірності для нормального закону розподілу; обирається на основі 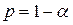 ;
;
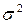 – дисперсія.
– дисперсія.
Практично для оцінки дисперсії беруть невелику пробну вибірку, на основі якої і робиться оцінка необхідного об’єму вибірки.
Для вибірки без повернення
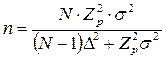 ,
,
де 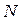 – число елементів генеральної сукупності. А, оскільки,
– число елементів генеральної сукупності. А, оскільки, 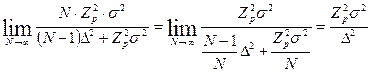 , то для достатньо великих вибірок різниця між методами стирається.
, то для достатньо великих вибірок різниця між методами стирається.
Статистичні показники, що розкривають властивості вибірок можна згрупувати в 3 групи:
– емпіричні розподіли, що характеризують структуру досліджуваної властивості;
– вибіркові показники, які представляють чисельні значення типових властивостей вибірки;
– кореляційно-регресійні показники, які дають можливості встановлювати взаємозв’язки між величинами.
Емпіричні дані, отримані шляхом вимірювання, повинні пройти первинну обробку та систематизацію, а саме:
– внесення даних в табличку форм (табуляція);
– впорядкування у варіаційні послідовності (ряди);
– представлення у вигляді розподілів.
Варіаційний ряд – це впорядкована за збільшенням, або зменшенням послідовність значень досліджуваної змінної.
Статистичний розподіл – це математична модель у вигляді співвідношення значень змінної «X», що характеризує властивості вибірки, до частот їх появи. Також використовується термін накопичена частота або інтегральна частота, яка характеризує кількість варіантів менших та рівних заданому.
Зведення – друга стадія (етап) статистичного дослідження. Воно передбачає узагальнення статистичних даних, перехід від індивідуальних значень показників до характеристики сукупності загалом або її окремих частин. Зведення у вузькому розумінні слова – це підрахунок підсумку, тобто сумування індивідуальних значень показника. Зведення у широкому розумінні – етап статистичного дослідження, на якому узагальнюються результати спостереження. У статистичній практиці виділяють два види зведення: просте і складне. Просте зведення полягає у підрахунку узагальнюючих показників шляхом сумування. Складне зведення передбачає групування одиниць сукупності з підрахунком сумарних значень як по кожній групі, так і по сукупності в цілому.
Статистичним групуванням називають розчленування, розподіл одиниць сукупності на класи, групи та підгрупи за суттєвими ознаками. Та ознака, котру покладено в основу групування, тобто за якою утворюються групи, є групувальною.
За допомогою групувань вирішують три завдання: виділення соціально-економічних типів явищ та процесів; вивчення складу та структури сукупності, структурних зрушень та закономірностей розподілу; виявлення взаємозв`язку між явищами або показниками, які їх характеризують. Кожному з названих завдань відповідає окремий вид групування – типологічне, структурне та аналітичне. Крім цього, групування класифікуються за видом групувальної ознаки, а також залежно від їхньої кількості та співвідношення.
За видом групувальної ознаки вони поділяються на групування за:
– атрибутивною ознакою;
– дискретною кількісною ознакою;
– інтервальною кількісною ознакою;
– альтернативною ознакою.
За числом групувальних ознак та співвідношенням між розрізняють групування: прості (групувальна ознака одна); багатомірні (ознак дві та більше, їх вагомість однакова); комбінаційні (ознак дві та більше, вони розглядаються у комбінації, тобто за однією ознакою утворюють групи, а за іншою – підгрупи); ієрархічні (ознак дві та більше, вони мають стале ієрархічне співвідношення).
До основних методологічних питань групування належать:
– вибір групувальної ознаки;
– визначення числа груп;
– встановлення інтервалів групування.
Інтервал групування – це проміжок між двома значеннями групувальної ознаки, в межах якого одиниці сукупності відносяться до даної групи. Відповідно менше та більше число мають назву нижньої та верхньої межі інтервалу, а різниця між ними називається величиною інтервалу. Інтервал групування називають закритим, якщо у ньому є нижня і верхня межа. У тому випадку, коли одна з меж відсутня, інтервал є відкритим зверху або знизу. Наприклад, групування робітників за рівнем місячної заробітної плати (грн.): до 650, 650-800, 800-1000, понад 1000. Інтервали називаються рівними, якщо їх величина у всіх групах однакова. У протилежному випадку утворюються нерівні інтервали, котрі в свою чергу бувають зростаючими або спадаючими.
Якщо виконується групування з рівними інтервалами, його величина визначається за формулою:
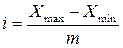 ,
,
де 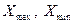 – відповідно найбільше (максимальне) та найменше (мінімальне) значення групувальної ознаки; m – число груп.
– відповідно найбільше (максимальне) та найменше (мінімальне) значення групувальної ознаки; m – число груп.
Вторинним групуванням називають групування, яке виконується не за первинними даними, а за вже згрупованими раніше. Воно здійснюються двома способами:
1) збільшенням або зменшенням інтервалів групування;
2) перегрупуванням за чисельністю або питомою вагою груп.
Результати зведення і групування переважно подаються у вигляді статистичних таблиць, які містять заголовки рядків (підмет таблиці) та заголовки граф (присудок таблиці), а у клітинках вміщують числа або позначки.
Для побудови оптимальної величини інтервалу «h» використовують емпіричну формулу Стерджеса:
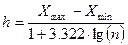 .
.
Під оптимальною величиною інтервалу розуміють таку величину, при якій побудований варіаційний ряд не буде надто громіздким, але дозволить виявити особливості вибірки. Якщо в результаті обчислень h – дробове число, то рекомендується використовувати або близький нескладний дріб, або для величин, що описуються значеннями набагато більшими за 1 близьке ціле число.
Існують загально прийняті способи графічного відображення варіаційних рядів. Використовуються наступні варіанти графічного зображення:
- полігон – як правило використовується лише для зображення дискретного варіаційного ряду. Для його побудови у прямокутній системі координат наносять точки з координатами: (Xi;mX) і з’єднують їх прямими відрізками;
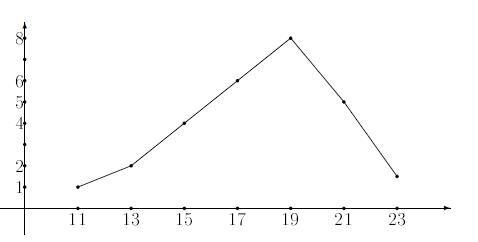
Рисунок 1.1 – Приклад полігона
- гістограма – використовується для зображення інтервального варіаційного ряду. Для її побудови у прямокутній системі координат по осі абсцис (X) відкладають відрізки, що відображають інтервали. На цих відрізках будують прямокутники з висотами рівними частотам або частотностям інтервалів
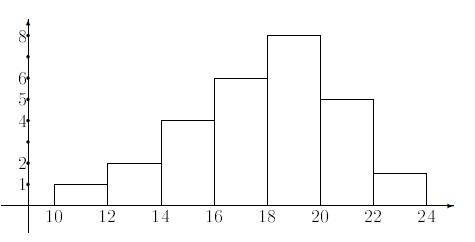
Рисунок 1.2 – Приклад гістограми
- кумулятивна крива – крива накопичення частот або частотностей.
- огіва – якщо в кумулятивної кривої змінити місцями осі координат, то одержана крива називається огівою.
Середні величини
Статистичний показник — це одна з основний категорій статистики, яка характеризує суспільні явища та процеси у поєднанні кількісної та якісної визначеності.
Класифікація показників:
– за способом одержання показники поділяються на первинні та вторинні (похідні). Перші одержують шляхом статистичного спостереження, зведення та групування, а інші розраховуються на основі перших;
– за ознакою часу показники поділяються на моментні та інтервальні. Моментні показники дають кількісну характеристику явища на певний момент часу, а інтервальні — за період часу (доба, тиждень, декада, місяць, квартал, рік).
– за можливістю узагальнення (сумування) показники поділяються на адитивні та неадитивні. Значення адитивних показників можна додавати, оскільки їх сума має економічний зміст. Неадитивні показники не можна додавати. Абсолютні статистичні величини (показники) — це характеристики явищ і процесів, що виражають чисельність сукупності або її частин, а також розміри, обсяги та рівні первинних ознак. Вони поділяються на індивідуальні, групові та загальні (сумарні). Індивідуальна абсолютна величина (показник) відноситься до окремої одиниці сукупності. Групова та загальна відповідно характеризує окрему групу одиниць або сукупність загалом, їх одержують шляхом сумування індивідуальних величин в межах групи або сукупності. Загальна абсолютна величина має назву «обсяг ознаки». Абсолютні показники— це іменовані числа, які виражаються у натуральних, трудових та вартісних вимірниках (одиницях виміру). У разі потреби використовуються умовно-натуральні одиниці виміру. Тоді рівень ознаки обчислюється у одиницях певного еталону. Перехід від натуральних до умовно-натуральних одиниць виміру здійснюється з допомогою перехідних коефіцієнтів.
Відносні величини (показники) виражають кількісне співвідношення між однойменним або різнойменними ознаками, що характеризують досліджувані явища та процеси. Відносна величина використовується у тому випадку, коли треба охарактеризувати:
§ у скільки разів одна ознака більша або менша за іншу;
§ яку частину становить одна ознака відносно іншої;
§ скільки одиниць однієї ознаки припадає на 1, 100, 1000, 10000, 100000 одиниць іншої ознаки.
Відносну величину завжди одержують шляхом ділення, тому її можна подати у вигляді дробу ( 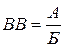 ). Показник, що знаходиться у чисельнику (А), називається порівнюваною величиною, а той, що стоїть у знаменнику (Б) — базою порівняння. Відповідно до обох величин використовуються різні форми виразу відносних величин, що дозволяє одержати її у зручному для сприйняття та інтерпретації вигляді – коефіцієнтному, процентному (відсотковому), промільному, продецімільному або просантимільному.
). Показник, що знаходиться у чисельнику (А), називається порівнюваною величиною, а той, що стоїть у знаменнику (Б) — базою порівняння. Відповідно до обох величин використовуються різні форми виразу відносних величин, що дозволяє одержати її у зручному для сприйняття та інтерпретації вигляді – коефіцієнтному, процентному (відсотковому), промільному, продецімільному або просантимільному.
Залежно від сутності та методики розрахунку розрізняють сім видів відносних величин: планового завдання або намірів, виконання плану або реалізації намірів, динаміки, структури, координації, порівняння та інтенсивності.
Відносна величина планового завдання або намірів показує, у скільки разів або на скільки процентів очікуваний рівень показника більший чи менший фактично досягнутого рівня. Цю відносну величину одержують шляхом ділення планового або очікуваного значення показника у наступному періоді до його фактичного значення у попередньому періоді.
Відносна величина виконання плану або реалізації намірів характеризує, у скільки разів або на скільки процентів фактичне значення показника більше або менше запланованого або очікуваного. Для одержання такої відносної величини необхідно фактичне значення показника розділити на планове або очікуване (за один період часу).
Відносна величина динаміки характеризує зміну показника у часі і визначається як відношення значення у наступному періоді до величини у попередньому періоді.
Відносна величина структури характеризує співвідношення частини та цілого. Вона показує, яку частину або скільки процентів становить певна складова від загального підсумку. Якщо ця відносна величина визначається у вигляді коефіцієнту, вона називається часткою, а якщо у процентах — питомою вагою. Сума відносних величин структури дорівнює 1 або 100%.
Відносна величина порівняння – це співвідношення однойменних показників, які обчислено по різних сукупностях або територіях за однаковий час.
Відносна величина інтенсивності визначається як відношення двох різних показників і переважно характеризує ступінь поширення чи розвитку явища у певному середовищі. Ця відносна величина може мати одиниці виміру вихідних показників.
Середня величина – це узагальнююча характеристика однорідної сукупності за варіюючою ознакою, котра показує типовий рівень цієї ознаки у одиниці сукупності. Ознака, за якою визначається середня величина, називається осереднюваної ознакою або осереднюваним показником.
При визначенні середньої величини необхідно дотримуватись двох головних вимог: по-перше, сукупність повинна бути якісно однорідною; по-друге, наявність достатньо великої кількості одиниць у сукупності, тобто масовість даних.
Середні величини поділяються на загальні та групові. Загальна середня величина характеризує сукупність в цілому, а групова – окрему групу одиниць. У статистичному аналізі використовують різні види середніх величин, які набувають одну із двох форм – просту або зважену (середня арифметична, середня гармонічна, середня геометрична, середня квадратична). Використання кожного виду середньої величини визначається характером вихідних даних (індивідуальні чи згруповані, прямі чи обернені, абсолютні чи відносні), а також характером зв'язку між індивідуальними значеннями та способом одержання обсягу ознаки на основі індивідуальних значень (сума прямих значень, сума обернених значень, сума квадратів, добуток).
Середня арифметична величина використовується у тому випадку, коли обсяг ознаки одержують як суму прямих індивідуальних значень. Середня арифметична величина має таку загальну логічну формулу:
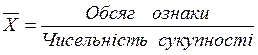 .
.
У тому випадку, коли середня величина визначається на основі індивідуальних даних, використовується середня арифметична проста:
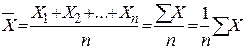 ,
,
де Х – індивідуальні значення осереднюваної ознаки; 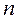 – кількість одиниць у сукупності.
– кількість одиниць у сукупності.
Якщо вихідні дані є результатом групування, тобто відомий дискретний або інтервальний ряд розподілу, використовується формула середньої арифметичної зваженої:
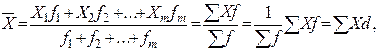
де Х– варіанти; 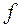 – частоти;
– частоти; 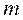 – число груп;
– число груп; 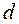 – частка групи.
– частка групи.
Якщо вихідні дані являють собою результат групування і відомі середні значення показника по кожній групі (групові середні), то розрахунок загальної середньої здійснюється виключно за формулою середньої арифметичної зваженої:

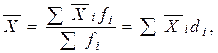
де 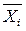 – групові середні величини;
– групові середні величини; 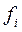 –число одиниць у і-тій групі;
–число одиниць у і-тій групі; 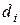 – частка і-тої групи.
– частка і-тої групи.
Математичні властивості середньої арифметичної використовуються для спрощення її розрахунку в рядах розподілу з рівними інтервалами (метод «моментів»). Середнє значення при використанні цього методу визначається за формулою:
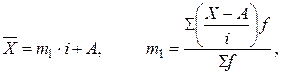
де m1 — момент першого порядку; і — величина інтервалу; А – середина центрального інтервалу або інтервалу з найбільшою частотою.
Середня гармонічна величина використовується у тому випадку, якщо відомі обернені значення осереднюваної ознаки. При цьому має місце така залежність:
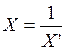 ,
,
де 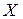 — значення прямої (осереднюваної) ознаки;
— значення прямої (осереднюваної) ознаки; 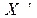 — значення оберненої ознаки.
— значення оберненої ознаки.
За наявності індивідуальних (незгрупованих) даних використовують середню гармонічну просту:
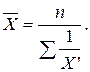
Для згрупованих даних (дискретних та інтервальних рядів розподілу) застосовують середню гармонічну зважену:
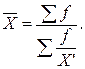
Для розрахунку середньої величини використовують також середню гармонічну такого виду:
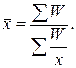
де W = Хf – обсяг ознаки; Х– значення осереднюваної ознаки.
Середня квадратична (проста і зважена) обчислюються за формулами:
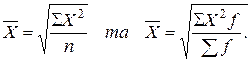
Вона використовується при розрахунках показників варіації (середнього квадратичного відхилення) у модифікованому вигляді.
Середня геометрична величина застосовується тоді, коли обсяг ознаки дорівнює не сумі, а добутку варіантів. Проста середня геометрична має вигляд:
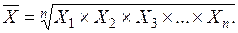
В окремих випадках виникає потреба визначити узагальнену середню величину по декількох ознаках одночасно. Вона має назву багатомірної середньої. При цьому осереднюються не абсолютні значення ознак, а коефіцієнти відношення до середнього рівня по кожній ознаці. Названі коефіцієнти визначаються за формулою:
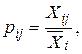
де і = 1, 2, 3, ....... , m – кількість ознак; j = 1, 2, 3, ....... , n – кількість одиниць у сукупності.
Багатомірна середня має вигляд:
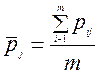 .
.
У статистичному аналізі досить часто необхідно визначати середнє значення не абсолютної, а відносної величини. Методика розрахунку середньої в даному випадку залежить від вихідних даних. Якщо відомі значення показників, котрі знаходяться у чисельнику та знаменнику відносної величини, використовується формула:
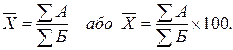
Якщо відомі значення осереднюваної відносної величини (ВВ), які розглядаються як варіанти 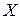 , та значення показника, котрий знаходиться у її знаменнику (Б) і виконує роль частоти f, розрахунок виконують за формулою середньої арифметичної зваженої:
, та значення показника, котрий знаходиться у її знаменнику (Б) і виконує роль частоти f, розрахунок виконують за формулою середньої арифметичної зваженої:
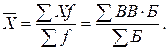
Для характеристики розподілу одиниць сукупності за певною ознакою використовується так звані порядкові або структурні середні – мода тамедіана.
Мода(М0) – це значення ознаки, яке найчастіше зустрічається у сукупності. Таким чином, у дискретному ряді розподілу – це варіант, який має найбільшу частоту. В інтервальному ряді розподілу мода знаходиться за формулою:
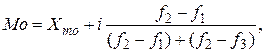
де Хмо – нижня межа модального інтервалу; і – величина модального інтервалу; f2, f1, f3 – відповідно частота модального, передмодального та післямодального інтервалів.
Медіана(Ме)–це значення ознаки, що ділить рангований ряд значень показника на дві рівні частини. У першої половини одиниць значення ознаки менше медіани, а у другої – більше, тобто, медіана – це значення ознаки, розміщене у середині рангованого ряду . У тому випадку, коли відомі індивідуальні значення ознаки, їх спочатку рангують (розміщують у порядку зростання чи спадання). Потім визначають номер (місце) медіани:
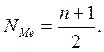
За непарної кількості одиниць медіана дорівнює значенню ознаки з порядковим номером (n+1)/2. За парної кількості одиниць у сукупності медіана визначається як півсума двох значень – з порядковими номерами n/2 та (n+2)/2:
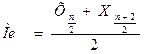
В інтервальному ряді розподілу медіана визначається за формулою:
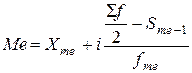
де Xme – нижня межа медіанного інтервалу; і – величина медіанного інтервалу; Sme- 1– нагромаджена частота передмедіанного інтервалу; fme – частота медіанного інтервалу.
Показники варіації
Під варіацією розуміють мінливість, коливання значень ознаки у одиниць сукупності. Варіацію можна вивчати як на основі рядів розподілу, так і за індивідуальними даними.
При вивченні варіації вирішуються три головних завдання (відповідно існує три групи показників):
– характеристики центру розподілу (середня, мода і медіана);
– характеристики розміру та ступеня варіації;
– характеристики виду та типу розподілу.
Для оцінювання розміру варіації використовується система абсолютних показників, які розглядаються як абсолютна міра варіації.
Розмах варіації ( 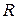 ) характеризує максимальну амплітуду коливань значень ознаки в сукупності:
) характеризує максимальну амплітуду коливань значень ознаки в сукупності:
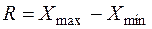
де: 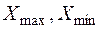 – відповідно найбільше та найменше значення ознаки.
– відповідно найбільше та найменше значення ознаки.
В інтервальних рядах розподілу розмах варіації визначається як різниця між верхньою межею останнього та нижньою межею першого інтервалу.
Середнє лінійне відхилення ( 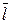 ), що характеризує середній розмір відхилень значень ознаки від середнього рівня. Для розрахунку за індивідуальними даними використовують середнє лінійне відхилення просте:
), що характеризує середній розмір відхилень значень ознаки від середнього рівня. Для розрахунку за індивідуальними даними використовують середнє лінійне відхилення просте:
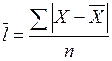 ,
,
де 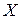 – індивідуальні значення ознаки;
– індивідуальні значення ознаки; 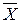 – середнє значення ознаки;
– середнє значення ознаки; 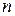 – кількість одиниць у сукупності.
– кількість одиниць у сукупності.
За наявності дискретного або інтервального ряду розподілу використовують середнє лінійне відхилення зважене:
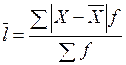 ,
,
де 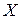 – варіанти;
– варіанти; 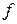 – частоти.
– частоти.
Дисперсія ( 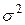 ) – це середній квадрат відхилень значень ознаки від її середнього рівня. Для розрахунку за індивідуальними даними використовують дисперсію просту:
) – це середній квадрат відхилень значень ознаки від її середнього рівня. Для розрахунку за індивідуальними даними використовують дисперсію просту:
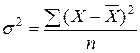 .
.
За наявності дискретного або інтервального ряду розподілу використовують дисперсію зважену:
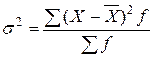 .
.
Для спрощення розрахунків використовують формули: 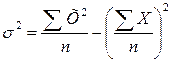 або
або 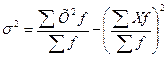 .
.
Середнє квадратичне відхилення (σ) — показує середній розмір відхилень значень ознаки від середнього рівня. Залежно від вихідних даних використовують середнє квадратичне відхилення просте і зважене (перший та другий вираз, відповідно):
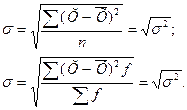
Середнє квадратичне відхилення найчастіше використовують у статистичному аналізі, тому його також називають стандартним відхиленням. Слід мати на увазі, що при симетричному розподілі одиниць сукупності 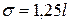 .
.
Відносні показники варіації використовуються:
– для оцінки ступеня варіації;
– для порівняння варіації різних ознак;
– для порівняння варіації однієї ознаки у різних сукупностях.
У статистичному аналізі найчастіше використовується такі відносні показники варіації:
– коефіцієнт осциляції: 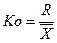 ;
;
– лінійний коефіцієнт варіації: 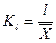 ;
;
– квадратичний коефіцієнт варіації: 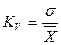 .
.
На практиці переважно використовують коефіцієнт варіації такого виду: 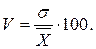
Вважається, що сукупність є однорідною, якщо V £ 33%. Крім цього, наведений коефіцієнт варіації застосовують для оцінки ступеня варіації: V < 15% – варіація слабка; 15 £ V £ 25% – середня; V > 25% – сильна.
Загальну варіацію ознаки можна розкласти на дві складові – систематичну та випадкову. Для цього необхідно виконати аналітичне групування, у якому досліджувана ознака є результативною, а групувальна ознака розглядається як систематичний фактор.
Випадкова варіація обумовлена дією випадкових факторів і проявляється у коливанні значень результативної ознаки в межах однієї групи. Вона характеризується показником внутрішньогрупової дисперсії та показує середній розмір відхилень значень результативної ознаки (у) від групової середньої ( 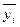 ):
): 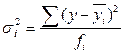 .
.
Внутрішньогрупову дисперсію розраховують окремо для кожної групи, тому для одержання її значення у сукупності визначають середню величину (середню внутрішньогрупову дисперсію): 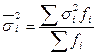 .
.
Доведено, що загальна дисперсія результативної ознаки дорівнює сумі міжгрупової дисперсії та середньої внутрішньогрупової дисперсії: 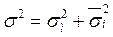
Це правило має назву «правило додавання дисперсій». Воно використовується для того, щоб розкласти загальну варіацію результативної ознаки на систематичну та випадкову. При цьому мірою систематичної варіації є міжгрупова дисперсія ( 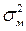 ), а випадкової – середня внутрішньогрупова дисперсія (
), а випадкової – середня внутрішньогрупова дисперсія ( 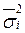 ).
).
Дата добавления: 2015-11-10; просмотров: 11224;
