Методы обхода деревьев

Систематический последовательный просмотр вершин дерева называется его обходом (walk) или прохождением (traversal). При обходе дерева каждая вершина обрабатывается один раз некоторым единым для всех вершин образом. Обход может быть, например, использован для контроля информации, хранящейся в элементах структуры, или для извлечения содержимого некоторого поля всех элементов с целью использования в другой процедуре.

При формулировании алгоритма обхода следует определить некоторый порядок, ориентируясь на который можно говорить об обработке следующего элемента дерева. Из структуры дерева, которая изображена на рисунке 9.7, вытекает три способа упорядочения:

1) сверху вниз (нисходящий): R, T₁, T₂, …, T_n (здесь R обозначает корень, T₁, T₂, …, T_n - поддеревья);

2) слева направо (смешанный): T₁, R , T₂, …, T_n;

3) снизу вверх (восходящий): T₁, T₂, …, T_n , R.

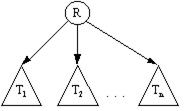
Рисунок 9.7 - Укрупненная структура дерева

Ниже приводятся рекурсивные формулировки методов обхода, различающиеся способом упорядочения дерева.

1) При нисходящем (прямом) обходе сначала посещается и обрабатывается корень R, затем выполняется нисходящий обход самого левого поддерева T₁, далее - нисходящий обход поддерева T₂, расположенного правее и т. д. Последним обходится нисходящим методом самое правое поддерево T_n. В соответствии с таким определением вершины дерева, изображенного на рисунке 9.1, при нисходящем обходе будут обрабатываться в следующем порядке: A, B, E, H, F, C, D,G.

2) Смешанный обход выполняется следующим образом: смешанный обход самого левого поддерева T₁, обработка корня R, смешанный обход поддерева T₂, расположенного правее T₁, и т. д. В конце смешанным методом обходится самое правое поддерево T_n. Последовательность обработки вершин того же самого дерева следующая: H, E, B, F, A, C, G, D.

3) Во время выполнения восходящего или обратного обхода обходятся восходящим методом все поддеревья в последовательности их расположения слева направо (T₁, T₂, …, T_n ), последним обрабатывается корень R. При этом последовательность поступления на обработку вершин того же дерева на рисунке 9.1 будет следующая: H, E, F, B, C, G, D, A.

Существует еще один - четвертый - метод обхода, который называется обходом по уровням, он наиболее прост для визуального представления, но наиболее сложен для программной реализации. Этот алгоритм предполагает обработку каждого из узлов, начиная с корневого, и просмотр вершин сверху вниз, уровень за уровнем. На каждом уровне вершины обрабатываются слева направо. При обходе этим методом дерева на рисунке 10.1 вершины будут обрабатываться в следующем порядке: A, B, C, D, E, F, G, H.

Если во всех вышеприведенных рекурсивных определениях методов обхода поменять местами слово «левый» на «правый» и наоборот, то получим определение трех других методов обхода, называемых соответственно обратным нисходящим, обратным смешанным и обратным восходящим методами.