Представление дерева в памяти

9.2.1 Естественное представление дерева

Дерево может быть представлено в машинной памяти в форме многосвязного списка, в котором каждый логический указатель соответствует ребру древовидного графа. При таком представлении каждому узлу дерева ставится в соответствие элемент многосвязного списка, причем в каждом элементе резервируются следующие поля:

- поля, содержащие полезные данные;

- поле степени исхода;

- поля логических указателей; их общее число в одном узле равно степени дерева, но в каждый момент времени количество непустых логических указателей равно степени исхода соответствующей вершины дерева.

На рисунке 9.3 показана логическая структура спискового представления дерева, изображенного на рисунке 9.1. Такое представление называют естественным представлением дерева. Все элементы дерева при этом имеют один и тот же тип. Тип элемента дерева, назовем этот тип Tvertex, называется базовым типом для дерева.

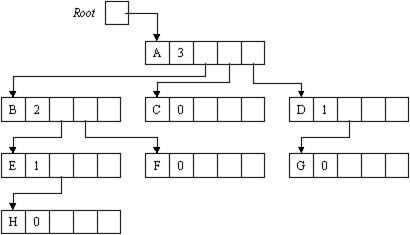
Рисунок 9.3 - Естественное представление дерева

Теперь можно сформулировать рекурсивное определение дерева: дерево типа Tvertex - это

а) либо пустое дерево,

б) либо некоторая вершина типа Tvertex, называемая корнем, с конечным числом связанных с ней поддеревьев, имеющих базовый тип Tvertex.

При естественном списковом представлении дерева обязательно должен быть организован указатель (курсор) на корневую вершину, обеспечивающий доступ к дереву. На рисунке 9.3 курсором корня является указатель Root. Иногда в элементе списка, соответствующем вершине дерева, размещают указатель, направленный к родительскому узлу, - это упрощает реализацию некоторых алгоритмов обработки деревьев.

Базовый тип (Tvertex) и курсор корня (Root) для дерева степени 3 можно описать нотациями языка Pascal, представленными ниже. Очевидно, при таком объявлении типа Tvertex количество полей для размещения структурных указателей фиксируется описанием типа Pchild. Если имеются основания предполагать, что при выполнении операций в дереве степень дерева потребуется увеличить, то это нужно предусмотреть в описании типа Pchild.

Type

Pvertex = ^Tvertex;

Pchild = Array [0..2] Of Pvertex;

Tvertex = Record

Dat: <поля данных>;

CountChild: Integer;

arrPchild: Pchild;

End;

Var Root: Pvertex;

9.2.2 Представление дерева с помощью вектора

Возможно, самым простым представлением дерева будет одномерный массив (вектор), в котором каждый элемент соответствует отдельной вершине и содержит два поля: поле данных и поле курсора родителя. Поле курсора некоторого элемента будет содержать индекс того элемента, который является родителем данного элемента. Если предположить, что поле Dat предназначено для хранения меток вершин дерева, то векторное представление дерева, показанного на рисунке 9.1, может быть представлено рисунком 9.4.

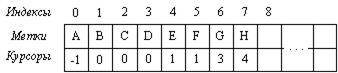
Рисунок 9.4 - Представление дерева с помощью вектора, в котором
каждая вершина содержит курсор на вершину‑родитель в виде его индекса

Поскольку элемент-корень не имеет родительского узла, то его курсор равен -1, т. е. он не указывает ни на какую другую вершину дерева. Такое представление использует то свойство деревьев, что каждая вершина, отличная от корня, имеет только одного родителя. Используя это представление можно легко организовать переходы от вершины к ее родителю, от него - к его родителю и т. д. С другой стороны, использование встроенных курсоров на родителей делает крайне сложными алгоритмы переходов от родителей к сыновьям.

Такой массив для дерева может быть объявлен следующим образом:

Type

Tvertex = Record

Dat: <поля данных>;

РarentCursor: Integer;

End;

Ttree = Array [0..maxVertex] Of Tvertex;

Var Tree: Ttree;

Если необходимо организовать переходы от родителей к сыновьям, то в дополнение к имеющимся полям (поле курсора на родителя можно оставить) следует добавить поля курсоров на сыновей, число которых соответствует максимально возможной степени дерева. В этом случае дерево можно описать следующим образом:

Type

TchildCursors = Array[0..maxChild] Of Integer;

Tvertex = Record

Dat: <поля данных>;

РarentCursor: Integer;

ChildCursors: TchildCursors;

End;

Ttree = Array [0..maxVertex] Of Tvertex;

Var Tree: Ttree;

В этом случае логическая структура дерева из рассматриваемого примера, может быть представлена рисунком 9.5.

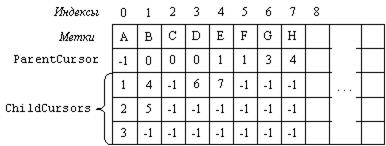
Рисунок 9.5 - Представление дерева с помощью вектора, в котором каждая
вершина содержит курсоры как на родительские вершины, так и на вершины-сыновья

Очевидно, старшинство сыновей, на которые указывают курсоры, возрастает с увеличением индекса поля-массива ChildCursors. Несуществующим (пустым) ссылкам соответствует значение курсора -1.

Легко заметить, что повышение гибкости такого представления по сравнению с предыдущим вариантом векторной организации связано с дополнительными затратами памяти, вызванными необходимостью хранения пустых ссылок.

9.2.3 Представление дерева с использованием списков сыновей

Важный и полезный способ представления деревьев состоит в формировании для каждого узла списка его сыновей. Эти списки можно представить векторным методом, но так как число сыновей у разных вершин может быть разное, обычно для этих целей применяются связные списки.

На рисунке 9.6 показано, каким способом представить дерево, изображенное на рисунке 9.1. Здесь имеет место индексированный вектор заголовков, в котором размещаются метки, играющие роль полезных данных. Каждый элемент такого вектора, называемый заголовком (header) содержит указатель, являющийся указателем связного списка. Элементы каждого списка являются сыновьями узла, соответствующего элементу заголовка. Например, узлы E и F - сыновья узла B.

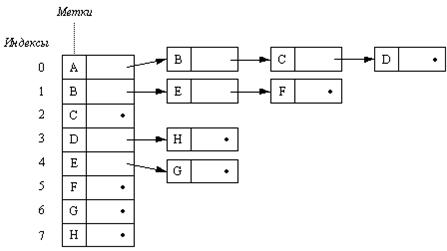
Рисунок 9.6 - Представление дерева со списком сыновей